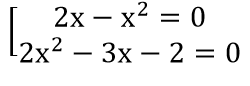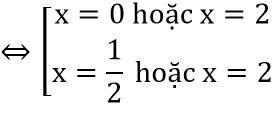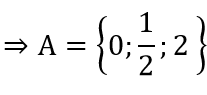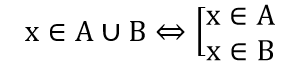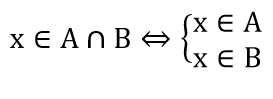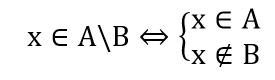Các dạng bài tập về Tập hợp chọn lọc có lời giải - Toán lớp 10
Các dạng bài tập về Tập hợp chọn lọc có lời giải
Với Các dạng bài tập về Tập hợp chọn lọc có lời giải Toán lớp 10 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tập hợp từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

- Lý thuyết Tập hợp và các phép toán trên tập hợp Xem chi tiết
- Dạng 1: Cách xác định tập hợp Xem chi tiết
- Dạng 2: Các phép toán trên tập hợp Xem chi tiết
- Dạng 3: Giải toán bằng biểu đồ Ven Xem chi tiết
- Bài tập Tập hợp và các phép toán trên tập hợp (có đáp án) Xem chi tiết
Cách xác định, cách viết tập hợp
Phương pháp giải
1: Với tập hợp A, ta có 2 cách:
Cách 1: liệt kê các phần tử của A: A={a1; a2; a3;..}
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của A
2:Tập hợp con
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B, kí hiệu là A ⊂ B.
A ⊂ B ⇔ ∀x : x ∈ A ⇒ x ∈ B.
A ⊄ B ⇔ ∀x : x ∈ A ⇒ x ∉ B.
Tính chất:
1) A ⊂ A với mọi tập A.
2) Nếu A ⊂ B và B ⊂ C thì A ⊂ C.
3) ∅ ⊂ A với mọi tập hợp A.
Ví dụ minh họa
Ví dụ 1: Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó:
a) A={x ∈ R|(2x - x2 )(2x2 - 3x - 2)=0}.
b) B={n ∈ N|3 < n2 < 30}.
Hướng dẫn:
a) Ta có:
(2x - x2 )(2x2 - 3x - 2) =0 ⇔
⇔
⇒
b) 3 < n2 < 30 ⇒ √3 < |n| < √30
Do n ∈ N nên n ∈ {2;3;4;5}
⇒ B = {2;3;4;5}.
Ví dụ 2: Viết mỗi tập hợp sau bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó:
a) A = {2; 3; 5; 7}
b) B = {-3; -2; -1; 0; 1; 2; 3}
c) C = {-5; 0; 5; 10; 15}.
Hướng dẫn:
a) A là tập hợp các số nguyên tố nhỏ hơn 10.
b) B là tập hơp các số nguyên có giá trị tuyệt đối không vượt quá 3.
B={x ∈ Z||x| ≤ 3}.
c) C là tập hợp các số nguyên n chia hết cho 5, không nhỏ hơn -5 và không lớn hơn 15.
C={n ∈ Z|-5 ≤ n ≤ 15; n ⋮ 5}.
Ví dụ 3: Cho tập hợp A có 3 phần tử. Hãy chỉ ra số tập con của tập hợp A.
Hướng dẫn:
Giả sử tập hợp A={a;b;c}. Các tập hợp con của A là:
∅ ,{a},{b},{c},{a;b},{b;c},{c;a},{a;b;c}
Tập A có 8 phần tử
Chú ý: Tổng quát, nếu tập A có n phần tử thì số tập con của tập A là 22 phần tử.
Cách giải bài tập các phép toán trên tập hợp
Phương pháp giải
Hợp của 2 tập hợp:
x ∈ A ∪ B ⇔
Giao của 2 tập hợp
x ∈ A ∩ B ⇔
Hiệu của 2 tập hợp
x ∈ A \ B ⇔
Phần bù
Khi B ⊂ A thì A\B gọi là phần bù của B trong A, kí hiệu là CA B.
Ví dụ minh họa
Ví dụ 1: Cho A là tập hợp các học sinh lớp 10 đang học ở trường em và B là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Hãy diễn đạt bằng lời các tập hợp sau: A ∪ B;A ∩ B;A \ B;B \ A.
Hướng dẫn:
1. A ∪ B: tập hợp các học sinh hoặc học lớp 10 hoặc học môn Tiếng Anh của trường em.
2. A ∩ B: tập hợp các học sinh lớp 10 học môn Tiếng Anh của trường em.
3. A \ B: tập hợp các học sinh học lớp 10 nhưng không học môn Tiếng Anh của trường em.
4. B \ A: tập hợp các học sinh học môn Tiếng Anh của trường em nhưng không học lớp 10 của trường em.
Ví dụ 2: Cho hai tập hợp:
A = { x ∈ R | x2 - 4x + 3 = 0};
B = { x ∈ R | x2 - 3x + 2 = 0}.
Tìm A ∪ B ; A ∩ B ; A \ B ; B \ A.
Hướng dẫn:
Ta có: A={1;3} và B={1;2}
A ∪ B={1;2;3}
A ∩ B={1}
A \ B={3}
B \ A={2}
Ví dụ 3: Cho đoạn A=[-5;1] và khoảng B =(-3; 2). Tìm A ∪ B; A ∩ B.
Hướng dẫn:
A ∪ B=[-5;2)
A ∩ B=(-3;1]
Cách giải toán bằng biểu đồ Ven
Phương pháp giải
- Vẽ các vòng tròn đại diện các tập hợp (mỗi vòng tròn là một tập hợp) lưu ý 2 vòng tròn có phần chung nếu của 2 tập hợp khác rỗng.
- Dùng các biến để chỉ số phần tử của từng phần không giao nhau.
- Từ giả thiết bài toán, lập hệ phương trình và giải tìm các biến.
Ví dụ minh họa
Ví dụ 1:Trong kì thi học sinh giỏi cấp trường, lớp 10A có 17 bạn được công nhận học sinh giỏi văn, 25 bạn học sinh giỏi toán. Tìm số học sinh đạt cả 2 giải văn và toán, biết lớp 10A có 45 bạn và có 13 bạn không đạt học sinh giỏi.
Hướng dẫn:
Biểu diễn tập hợp các học sinh giỏi văn và các học sinh giỏi toán bằng 2 đường cong kín và tập hợp các học sinh lớp 10A bằng hình chữ nhật như hình bên dưới.
Gọi x là số học sinh giỏi văn không giỏi toán; y là số học sinh giỏi cả văn và toán; z là số học sinh chỉ giỏi toán mà không giỏi văn và t là số học sinh không đạt học sinh giỏi.
Theo biểu đồ giả thiết, ta có:
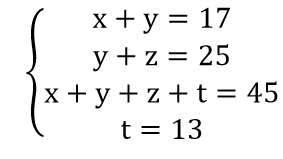
Cộng (1) với (2) rồi trừ cho (3) ta được: 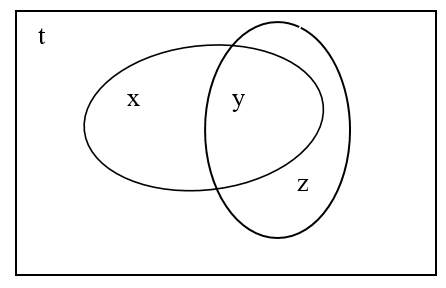
(x + y) + (y + z) – (x + y + z + t) = 17 + 25 - 45
⇒ y - t = - 3 ⇒ y = t – 3 = 10
Vậy lớp 10A có 10 học sinh giỏi cả 2 môn văn và toán.