Tìm các vectơ cùng phương, cùng hướng, ngược hướng (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Tìm các vectơ cùng phương, cùng hướng, ngược hướng lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Tìm các vectơ cùng phương, cùng hướng, ngược hướng.

Tìm các vectơ cùng phương, cùng hướng, ngược hướng (bài tập + lời giải)

1. Phương pháp giải.

- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

- Hai vectơ cùng phương chỉ có thể cùng hướng hoặc ngược hướng.

- Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương.

2. Ví dụ minh họa.

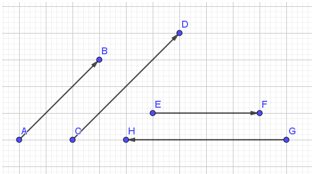
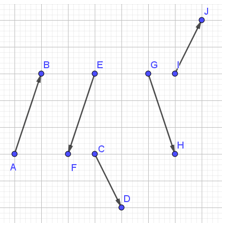
Ví dụ 1. Kể tên các cặp vectơ cùng phương trong hình vẽ sau và cho biết chúng cùng hướng hay ngược hướng.

Hướng dẫn giải:

Vectơ $\overrightarrow{AB}$ có giá là đường thẳng AB

Vectơ $\overrightarrow{CD}$ có giá là đường thẳng CD

Vectơ $\overrightarrow{EF}$ có giá là đường thẳng EF

Vectơ $\overrightarrow{GH}$ có giá là đường thẳng GH

Quan sát hình trên, ta có:

+) AB // CD nên $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương, chúng cũng cùng hướng từ dưới chéo lên trên nên hai vectơ này cùng hướng.

+) EF // GH nên $\overrightarrow{EF}$ và $\overrightarrow{GH}$ cùng phương, $\overrightarrow{EF}$ có hướng từ trái sang phải, $\overrightarrow{GH}$ có hướng từ phải sang trái. Do đó, $\overrightarrow{EF}$ và $\overrightarrow{GH}$ ngược hướng.

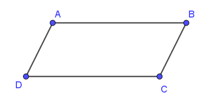
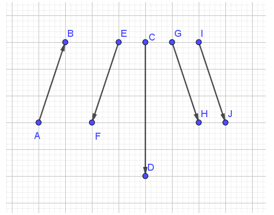
Ví dụ 2. Cho hình bình hành ABCD như hình vẽ. Vectơ nào cùng phương, ngược hướng với vectơ $\overrightarrow{AB}$.

Hướng dẫn giải:

Vectơ $\overrightarrow{AB}$ và vectơ $\overrightarrow{BA}$ cùng có giá là đường thẳng AB.

Mà ABCD là hình bình hành nên AB // CD.

Do đó, vectơ $\overrightarrow{AB}$ cùng phương với các vectơ $\overrightarrow{BA},\overrightarrow{CD},\overleftarrow{DC}$.

Mà vectơ $\overrightarrow{AB}$ có hướng từ trái sang phải, vectơ $\overrightarrow{BA}$ có hướng từ phải sang trái, vectơ $\overrightarrow{CD}$ có hướng từ phải sang trái, vectơ $\overrightarrow{DC}$ có hướng từ trái sang phải.

Vậy hai vectơ $\overrightarrow{BA},\overrightarrow{CD}$ là các vectơ cùng phương, ngược hướng với vectơ $\overrightarrow{AB}$.

3. Bài tập tự luyện.

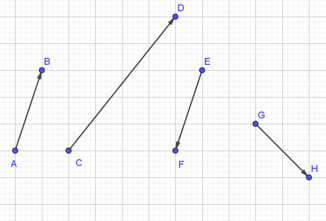
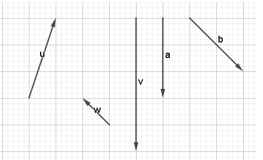
Bài 1. Trong hình vẽ sau, cặp vectơ cùng phương là:

A. $\overrightarrow{AB}$ và $\overrightarrow{CD}$;

B. $\overrightarrow{AB}$ và $\overrightarrow{EF}$;

C. $\overrightarrow{AB}$ và $\overrightarrow{GH}$;

D. $\overrightarrow{CD}$ và $\overrightarrow{GH}$.

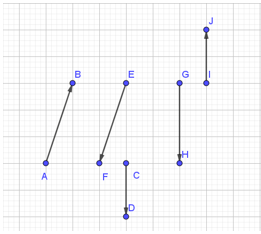
Bài 2. Trong hình vẽ sau, cặp vectơ nào dưới đây không cùng phương?

A. $\overrightarrow{AB}$ và $\overrightarrow{GH}$;

B. $\overrightarrow{AB}$ và $\overrightarrow{EF}$;

C. $\overrightarrow{GH}$ và $\overrightarrow{IJ}$;

D. $\overrightarrow{CD}$ và $\overrightarrow{GH}$.

Bài 3. Số cặp vectơ cùng phương trong hình vẽ sau là:

A. 2;

B. 3;

C. 1;

D. 4.

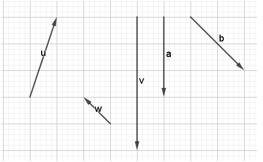
Bài 4. Số cặp vectơ cùng phương trong hình vẽ sau là:

A. 2;

B. 3;

C. 1;

D. 0.

Bài 5. Cho hình vẽ dưới đây.

Khẳng định nào sau đây là đúng ?

A. Trong hình có 3 cặp vectơ cùng phương;

B. $\overrightarrow{u}$ và $\overrightarrow{\text{w}}$ cùng phương;

C. $\overrightarrow{u}$ và $\overrightarrow{b}$ cùng phương;

D. $\overrightarrow{a}$ và $\overrightarrow{v}$ cùng phương.

Bài 6. Cho hình vẽ dưới đây.

Khẳng định nào sau đây là sai ?

A. Trong hình có 2 cặp vectơ cùng phương;

B. $\overrightarrow{b}$ và $\overrightarrow{\text{w}}$ cùng phương, ngược hướng;

C. $\overrightarrow{u}$ và $\overrightarrow{b}$ không cùng phương;

D. $\overrightarrow{a}$$\overrightarrow{v}$ cùng phương, ngược hướng.

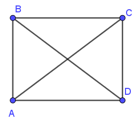
Bài 7. Cho hình chữ nhật ABCD như hình vẽ.

Khẳng định nào sau đây là đúng ?

A. $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương ngược hướng;

B. $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương cùng hướng;

C. $\overrightarrow{AC}$ và $\overrightarrow{BD}$cùng phương ngược hướng;

D. $\overrightarrow{AC}$ và $\overrightarrow{BD}$ cùng phương cùng hướng.

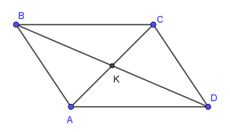
Bài 8. Cho hình bình hành ABCD có K là giao điểm hai đường chéo như hình vẽ.

Khẳng định nào sau đây là đúng ?

A. $\overrightarrow{AK}$ và $\overrightarrow{KC}$ cùng phương ngược hướng;

B. $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương cùng hướng;

C. $\overrightarrow{KC}$ và $\overrightarrow{KA}$ cùng phương ngược hướng;

D. $\overrightarrow{AC}$ và $\overrightarrow{BD}$ cùng phương cùng hướng.

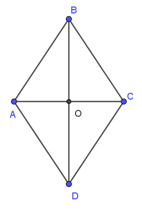
Bài 9. Cho hình thoi ABCD có O là giao điểm của hai đường chéo như hình vẽ.

Khẳng định nào sau đây là sai ?

A. $\overrightarrow{OC}$ và $\overrightarrow{AC}$ cùng phương cùng hướng;

B. $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương ngược hướng;

C. $\overrightarrow{OC}$ và $\overrightarrow{OA}$ cùng phương cùng hướng;

D. $\overrightarrow{OD}$ và $\overrightarrow{BD}$ cùng phương cùng hướng.

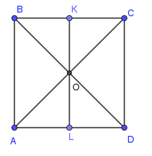
Bài 10. Cho hình vuông ABCD có tâm O, K và L lần lượt là trung điểm của BC và AD như hình vẽ.

Khẳng định nào sau đây là sai ?

A. $\overrightarrow{OL}$ và $\overrightarrow{KO}$ cùng phương cùng hướng;

B. $\overrightarrow{KO}$ và $\overrightarrow{CD}$ cùng phương ngược hướng;

C. $\overrightarrow{OL}$ và $\overrightarrow{BA}$ cùng phương cùng hướng;

D. $\overrightarrow{OL}$ và $\overrightarrow{CD}$ cùng phương cùng hướng.