Tìm tổng của hai hay nhiều vectơ (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Tìm tổng của hai hay nhiều vectơ lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Tìm tổng của hai hay nhiều vectơ.

Tìm tổng của hai hay nhiều vectơ (bài tập + lời giải)

1. Phương pháp giải

Để tìm tổng của hai hay nhiều vectơ, ta áp dụng các định nghĩa, quy tắc và tính chất sau:

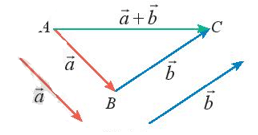
- Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$. Từ một điểm A tùy ý, lấy hai điểm B, C sao cho $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{BC}=\overrightarrow{b}$. Khi đó $\overrightarrow{AC}$ được gọi là tổng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ và được kí hiệu là $\overrightarrow{a}$ + $\overrightarrow{b}$. Vậy $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.

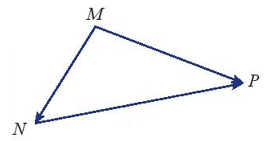
- Quy tắc ba điểm: Với ba điểm M, N, P có: $\overrightarrow{MN}+\overrightarrow{NP}=\overrightarrow{MP}$.

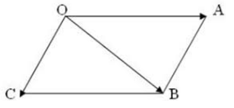
- Quy tắc hình bình hành: Nếu OABC là hình bình hành thì ta có: $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}$

- Tính chất của phép cộng các vectơ:

+ Tính chất giao hoán: $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}$;

+ Tính chất kết hợp: $\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)$;

+ Với mọi vectơ  ta luôn có: $\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a}$.

+ Tổng của hai vectơ đối nhau luôn bằng vectơ $\overrightarrow{0}$: $\overrightarrow{a}+\left(-\overrightarrow{a}\right)=\overrightarrow{0}$.

- Chú ý:

+ Khi cộng hai vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.

+ Để áp dụng quy tắc hình bình hành, ta cần đưa bài toán tìm tổng hai vectơ về bài toán tìm tổng của hai vectơ có chung điểm đầu.

2. Ví dụ minh họa

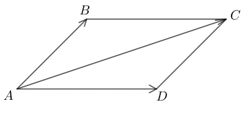
Ví dụ 1. Cho hình bình hành ABCD. Tính:

a) $\overrightarrow{AB}+\overrightarrow{BC}$;

b) $\overrightarrow{AB}+\overrightarrow{AD}$.

Hướng dẫn giải:

a) Áp dụng quy tắc ba điểm cho ba điểm A, B, C có:

$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.

b) Áp dụng quy tắc hình bình hành cho hình bình hành ABCD ta có:

$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$.

Ví dụ 2. Cho 4 điểm A, B, C, E phân biệt. Tính $\overrightarrow{AB}+\overrightarrow{CE}+\overrightarrow{BC}$.

Hướng dẫn giải:

Ta có:

$\overrightarrow{AB}+\overrightarrow{CE}+\overrightarrow{BC}$

$=\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{CE}$(tính chất giao hoán và kết hợp)

$=\overrightarrow{AC}+\overrightarrow{CE}$    (quy tắc ba điểm)

$=\overrightarrow{AE}$

Vậy $\overrightarrow{AB}+\overrightarrow{CE}+\overrightarrow{BC}=\overrightarrow{AE}$.

3. Bài tập tự luyện

Bài 1. Cho O là trung điểm của AB. Ta có: $\overrightarrow{AB}+\overrightarrow{OA}=?$

A. $\overrightarrow{AB}$;

B. $\overrightarrow{OA}$;

C. $\overrightarrow{BO}$;

D. $\overrightarrow{OB}$.

Bài 2. Cho 4 điểm A, B, C, D. Ta có: $\overrightarrow{AB}+\overrightarrow{BD}=?$

A. $\overrightarrow{AC}+\overrightarrow{BD}$;

B. $\overrightarrow{AD}+\overrightarrow{DB}$;

C. $\overrightarrow{AC}+\overrightarrow{CD}$;

D. $\overrightarrow{DA}+\overrightarrow{DB}$.

Bài 3. Cho các điểm A, B, C phân biệt. Đẳng thức nào sau đây đúng ?

A. $\overrightarrow{AB}=\overrightarrow{BC}+\overrightarrow{CA}$;

B. $\overrightarrow{AB}=\overrightarrow{CB}+\overrightarrow{AC}$;

C. $\overrightarrow{AB}=\overrightarrow{BC}+\overrightarrow{AC}$;

D. $\overrightarrow{AB}=\overrightarrow{CA}+\overrightarrow{BC}$.

Bài 4. Cho hình bình hành ABCD tâm O. Khi đó, $\overrightarrow{OA}+\overrightarrow{BO}=?$

A. $\overrightarrow{OC}+\overrightarrow{OB}$;

B. $\overrightarrow{AB}$;

C. $\overrightarrow{OC}+\overrightarrow{DO}$;

D. $\overrightarrow{CD}$.

Bài 5. Cho hình vuông ABCD tâm O. Khi đó: $\overrightarrow{AB}+\overrightarrow{AD}=?$

A. $\overrightarrow{AB}$;

B. $\overrightarrow{BC}$;

C. $\overrightarrow{BD}$;

D. $\overrightarrow{AC}$.

Bài 6. Cho 6 điểm A, B, C, D, E, F. Đẳng thức nào sau đây đúng.

A. $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{FA}+\overrightarrow{BC}+\overrightarrow{EF}+\overrightarrow{DE}=\overrightarrow{0}$;

B. $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{FA}+\overrightarrow{BC}+\overrightarrow{EF}+\overrightarrow{DE}=\overrightarrow{AE}$;

C. $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{FA}+\overrightarrow{BC}+\overrightarrow{EF}+\overrightarrow{DE}=\overrightarrow{AF}$;

D. $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{FA}+\overrightarrow{BC}+\overrightarrow{EF}+\overrightarrow{DE}=\overrightarrow{AD}$.

Bài 7. Cho các điểm M, N, P, Q, R. Tính $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}$ = ?

A. $\overrightarrow{MR}$;

B. $\overrightarrow{MQ}$;

C. $\overrightarrow{MP}$;

D. $\overrightarrow{MN}$.

Bài 8. Cho hình bình hành ABCD tâm O. Khẳng định nào sau đây là đúng ?

A. $\overrightarrow{AO}+\overrightarrow{BO}=\overrightarrow{BD}$;

B. $\overrightarrow{AO}+\overrightarrow{AC}=\overrightarrow{BO}$;

C. $\overrightarrow{OB}+\overrightarrow{AO}=\overrightarrow{CD}$;

D. $\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{DA}$.

Bài 9. Cho 4 điểm A, B, C, D. Ta có: $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{DA}+\overrightarrow{BC}=?$

A. $\overrightarrow{DB}$;

B. $\overrightarrow{BD}$;

C. $\overrightarrow{0}$;

D. $\overrightarrow{DA}$.

Bài 10. Cho hình bình hành ABCD, M, N lần lượt là trung điểm của AD và BC. Khi đó, $\overrightarrow{AD}+\overrightarrow{MB}+\overrightarrow{NA}=?$

A. $\overrightarrow{DB}$;

B. $\overrightarrow{MN}$;

C. $\overrightarrow{0}$;

D. $\overrightarrow{DA}$.