Tính độ dài của tổng và hiệu hai hay nhiều vectơ (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Tính độ dài của tổng và hiệu hai hay nhiều vectơ lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Tính độ dài của tổng và hiệu hai hay nhiều vectơ.

Tính độ dài của tổng và hiệu hai hay nhiều vectơ (bài tập + lời giải)

1. Phương pháp giải

- Độ dài của vectơ là độ dài đoạn thẳng tạo bởi điểm đầu và điểm cuối của vectơ đó.

 $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{BA}\right|=AB=BA$.

- Để tính độ dài của tổng và hiệu hai hay nhiều vectơ, trước hết, ta biến đổi tổng hoặc hiệu của các vectơ đã cho về một vectơ, sau đó tính độ dài của vectơ vừa tìm được.

$\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{c}\Rightarrow \left|\overrightarrow{a}+\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|$.

• Ta thường sử dụng các quy tắc sau để biến đổi:

- Quy tắc ba điểm: Với 3 điểm A, B, C ta luôn $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, $\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}$.

- Quy tắc hình bình hành: Cho hình bình hành ABCD, ta có $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$.

- Quy tắc trung điểm: $\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$ với I là trung điểm của AB.

- Quy tắc trọng tâm: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ với G là trọng tâm của tam giác ABC.

- Sử dụng các tính chất của phép cộng, phép trừ hai vectơ.

• Để tính độ dài đoạn thẳng: Ta thường sử dụng các công thức về cạnh như hệ thức lượng tam giác vuông, định lý Py-ta-go, tính chất tam giác đều, hình chữ nhật, hình vuông,…

2. Ví dụ minh họa

Ví dụ 1. Cho tam giác đều ABC cạnh a. Tính $\left|\overrightarrow{AB}-\overrightarrow{AC}\right|$

Hướng dẫn giải:

Ta có:

$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$

$\Rightarrow \left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CB}\right|=CB=a$ (do tam giác ABC đều).

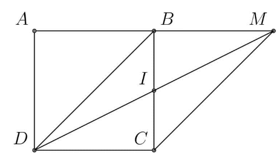
Ví dụ 2. Cho hình vuông ABCD cạnh a. Tính $\left|\overrightarrow{DB}+\overrightarrow{DC}\right|$

Hướng dẫn giải:

Dựng hình bình hành CDBM thì DM cắt BC tại trung điểm I của mỗi đường.

Theo quy tắc hình bình hành ta có: $\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{DM}$ nên $\left|\overrightarrow{DB}+\overrightarrow{DC}\right|=\left|\overrightarrow{DM}\right|=DM=2DI$.

Ta có: CI = $\frac{1}{2}$BC = $\frac{a}{2}$ (do I là trung điểm của BC).

Áp dụng định lí Pythagore trong tam giác vuông DCI ta được:

$D{I}^2=D{C}^2+C{I}^2=a^2+{\left(\frac{a}{2}\right)}^2=\frac{5}{4}{a}^2\Rightarrow DI=\frac{a\sqrt{5}}{2}$

Vậy $\left|\overrightarrow{DB}+\overrightarrow{DC}\right|=2DI=2.\frac{a\sqrt{5}}{2}=a\sqrt{5}$.

3. Bài tập tự luyện

Bài 1. Cho hình vuông ABCD tâm I, có cạnh bằng a. Tính $\left|\overrightarrow{AB}+\overrightarrow{AD}\right|$.

A. $a\sqrt{2}$;

B. a;

C. 2a;

D. $\frac{a}{2}$.

Bài 2. Cho tam giác ABC vuông cân tại A có AB = a. Độ dài của vectơ $\overrightarrow{a}=\overrightarrow{AB}+\overrightarrow{AC}$ là:

A. $a\sqrt{2}$;

B. $\frac{a\sqrt{2}}{2}$;

C. 2a;

D. a.

Bài 3. Cho tam giác ABC vuông cân tại C và AB = $\sqrt{2}$. Tính $\left|\overrightarrow{AB}-\overrightarrow{AC}\right|$.

A. 3;

B. 1;

C. 2;

D. 4.

Bài 4. Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Độ dài của vectơ $\overrightarrow{u}=\overrightarrow{CA}+\overrightarrow{AB}$ bằng:

A. 2;

B. $2\sqrt{13}$;

C. 5;

D. $\sqrt{13}$.

Bài 5. Cho tam giác ABC có: AB = AC = a và $\widehat{BAC}=120°$. Ta có $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|$ = ?

A. $a\sqrt{3}$;

B. a;

C. $\frac{a}{2}$;

D. 2a.

Bài 6. Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính $\left|\overrightarrow{CA}-\overrightarrow{HC}\right|$.

A. $\frac{a}{2}$;

B. $\frac{3a}{2}$;

C. $\frac{2\sqrt{3}a}{3}$;

D. $\frac{a\sqrt{7}}{2}$.

Bài 7. Độ dài của vectơ $\overrightarrow{x}=\overrightarrow{IA}-\overrightarrow{IB}$ với I là trung điểm của đoạn thẳng AB = 4 là:

A. 2;

B. 4;

C. 3;

D. 6.

Bài 8. Cho hình vuông ABCD cạnh 2a. Tính $\left|\overrightarrow{AB}-\overrightarrow{DA}\right|$.

A. $a\sqrt{2}$;

B. a;

C. $2a\sqrt{2}$;

D. 2a.

Bài 9. Cho hình vuông ABCD cạnh bằng 2, có tâm O. Khi đó ta tính được $\left|\overrightarrow{BO}-\overrightarrow{BC}\right|=a\sqrt{2}.$Tính giá trị biểu thức A = 2a² – 5a.

A. 2;

B. $2\sqrt{2}$;

C. – 3;

D. 0.

Bài 10. Cho hình vuông ABCD cạnh 2, tâm O. Tính độ dài của vectơ $\overrightarrow{y}$ với $\overrightarrow{y}=\overrightarrow{BO}-\overrightarrow{BC}+\overrightarrow{OC}$. Khẳng định nào sau đây là đúng?

A. $\left|\overrightarrow{y}\right|$= 2;

B. $\left|\overrightarrow{y}\right|$= 2$\sqrt{2}$;

C. $\left|\overrightarrow{y}\right|$= $\sqrt{2}$;

D. $\left|\overrightarrow{y}\right|$= 0.