Cách tìm điểm đối xứng của 1 điểm qua đường thẳng cực hay - Toán lớp 10
Cách tìm điểm đối xứng của 1 điểm qua đường thẳng cực hay
Với Cách tìm điểm đối xứng của 1 điểm qua đường thẳng cực hay Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm điểm đối xứng của 1 điểm qua đường thẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 10.
A. Phương pháp giải
Cho điểm A và đường thẳng (d): ax + by + c = 0 . Tìm điểm M đối xứng với điểm A qua đường thẳng (d):
+ Bước 1: Lập phương trình đường thẳng AM:
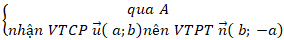
⇒ Phương trình (AM) .
+ Bước 2: Gọi H là hình chiếu của A trên d. Khi đó AM và d giao nhau tại H nên tọa độ H là nghiệm hệ phương trình:
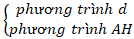
+ Bước 3: Do M đối xứng với A qua d nên H là trung điểm của AM.
Áp dụng công thức trung điểm đoạn thẳng ta được:
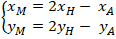
B. Ví dụ minh họa
Ví dụ 1: Cho đường thẳng d: 2x - 3y + 3 = 0 và M( 8; 2) . Tọa độ của điểm M’ đối xứng với M qua d là:
A. ( -4; 8 ) B. (-4; -8 ) C. ( 4; 8) D. (4; -8)
Lời giải
+Phương trình đường thẳng MM’:
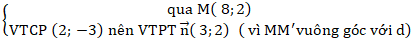
⇒ ( MM’) : 3( x - 8) + 2( y - 2) = 0 hay 3x + 2y - 28 = 0
+ Gọi H là hình chiếu của M lên d. Khi đó MM’ và d cắt nhau tại H nên tọa độ H là nghiệm hệ :
⇒ H(6; 5)
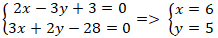
+ Khi đó H là trung điểm của đoạn MM’. Áp dụng công thức trung điểm ta suy ra
. Vậy M’( 4; 8) .
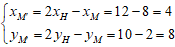
Chọn C.
Ví dụ 2: Cho điểm M(1; 2) và đường thẳng d: 2x + y - 5 = 0. Toạ độ của điểm đối xứng với điểm M qua d là:
A. (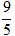
; 
)
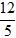
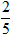
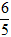
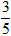
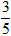
B. (- 
; 
)
C. (0; 
)
D. (
; - 5)
Lời giải
Ta thấy M ∉ d .
Gọi H( a; b) là hình chiếu của điểm M lên đường thẳng d MH→( a - 1; b - 2) .
Ta có đường thẳng d: 2x + y - 5 = 0 nên có vtpt: n→(2;1)
Suy ra u→( -1; 2) là vectơ chỉ phương của đường thẳng d.
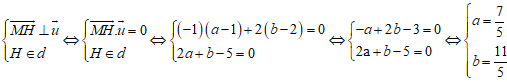
Do đó H(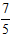
; 
) .
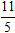
Gọi M’( x; y) đối xứng với M qua đường thẳng d . Khi đó ta có: H là trung điểm của MM’
Ta có: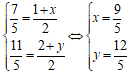 
Vậy tọa độ điểm đối xứng với M qua d là M'(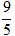
;
) .
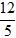
Chọn A.
Ví dụ 3 : Cho đường thẳng d: 2x - 3y + 3 = 0 và M( 8; 2) . Tọa độ của điểm M’ đối xứng với M qua d là
A. ( -4; 8) B. ( -4; -8) C. ( 4; 8) D. ( 4; -8)
Lời giải
+ Do M’ đối xứng với M qua d nên MM’ vuông góc với d.
+ Đường thẳng MM’: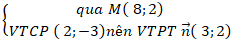 
⇒ MM’: 3( x - 8) + 2( y - 2) = 0 hay 3x + 2y - 28 = 0
+ Gọi H là giao điểm của MM’ và d. Khi đó tọa độ H là nghiệm hệ :
⇒ H( 6; 5)
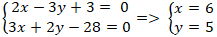
+ Do M’ đối xứng với M qua d nên H là trung điểm của MM’. Tọa độ điểm M’ là:
⇒ M’( 4; 8)
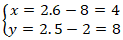
Chọn C.
Ví dụ 4: Cho điểm A( 1; 2) và đường thẳng (d): x + 2y - 3 = 0 .Tìm điểm đối xứng với A qua đường thẳng d.
A. ( 1; -2)
B. (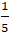 
; 
)
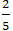
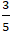
C. ( 
; 
)
D. Đáp án khác
Lời giải
+ Gọi H là hình chiếu của A lên đường thẳng (d) .
+ Lập phương trình đường thẳng AH:
( AH) :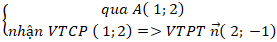 
⇒ Phương trình ( AH) : 2( x - 1) – 1.( y - 2) = 0 hay 2x - y = 0
+ Hai đường thẳng AH và d cắt nhau tại H nên tọa độ điểm H là nghiệm hệ phương trình:
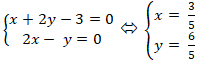
+ Gọi B đối xứng với A qua d. Khi đó; H là trung điểm của AB.
⇒ Tọa độ điểm B là: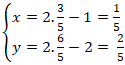 
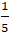
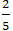
⇒ B(
;
)
Chọn B.
Ví dụ 5: Cho điểm A( 2; 0) và đường thẳng d: x + y - 2 = 0. Tìm điểm A’ đối xứng với điểm A qua đường thẳng d.
A. ( 2; -1) B. (2; 0) C. ( 1; -2) D. (-2; -1)
Lời giải
Ta có: 2 + 0 - 2 = 0 nên điểm A thuộc đường thẳng d.
⇒ Điểm đối xứng với điểm A qua đường thẳng d chính là điểm A.
Chọn B.
Ví dụ 6: Cho tam giác ABC có A( 0; -2).Gọi I ( 2; 4) là trung điểm của AB và J( -4; 2) là trung điểm của AC. Gọi điểm A’ đối xứng điểm A qua BC. Viết phương trình đường thẳng AA’?
A. 6x + 2y - 3 = 0 B. 6x + 2y + 4 =0 C. 2x - y + 1 = 0 D. Tất cả sai
Lời giải
+ Do I và J lần lượt là trung điểm của AB và AC nên IJ là đường trung bình của tam giác ABC ⇒ IJ// BC ( 1) .
+ Do A’ đối xứng với A qua BC
⇒ AA’ vuông góc BC (2).
Từ(1) và ( 2) suy ra: AA’ vuông góc IJ
+ Lập phương trình AA’: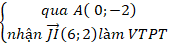
⇒ ( AA’): 6(x - 0) + 2( y + 2) = 0 hay 6x + 2y + 4 = 0.
Chọn B.
Ví dụ 7: Cho đường thẳng ∆ :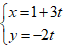 
và điểm M(1; 2). Tìm điểm đối xứng với M qua đường thẳng ∆ là:
A. (4; -2)
B. M’(- 
; 
)
C. M’(
;
)
D. M’(
; 
)
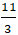
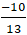
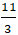
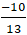
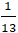
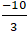
Lời giải
Gọi M’ đối xứng với M qua ∆.
+ Đường thẳng MM’: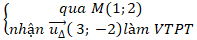 
⇒ Phương trình đường thẳng MM’:
3(x - 1) – 2(y - 2)= 0 hay 3x - 2y + 1 = 0.
+ Giao điểm H của đường thẳng MM’ và ∆ là nghiệm hệ:
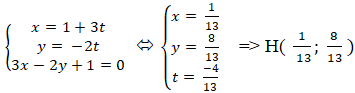
+ Điểm M đối xứng M’ qua ∆ nên H là trung điểm MM’. Suy ra tọa độ điểm M’:
⇒ M’(-
;
)
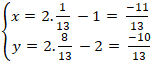
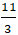
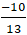
Chọn B.
Ví dụ 8: Cho tam giác ABC có AB = 6; BC = 6√2 và góc B = 450.Gọi A’ là điểm đối xứng với A qua BC. Tìm mệnh đề sai?
A. Tứ giác ACA’B là hình thoi
B. AA’ = 3
C. BA’ = 6
D. Tứ giác ACA’B là hình bình hành
Lời giải
+ Áp dụng định lí cosin vào tam giác ABC ta có:
AC2 = AB2 + BC2 – 2.AC.BC.Cos B
= 62 + (6√2)2 - 2.6.6√2.cos450 = 36
⇒ AC = 6 nên AB = AC = 6 và AB2 + AC2 = BC2
⇒ Tam giác ABC vuông cân tại A.
+ Gọi H là chân đường cao hạ từ điểm A lên BC.
AH là đường cao nên đồng thời là đường trung tuyến
⇒ H là trung điểm của BC: AH = BH = CH = BC/2 = 3√2 ⇒ AA’= 6√2
+ Do A’ đối xứng với điểm A qua BC nên H là trung điểm của AA’ và AA’; BC vuông góc với nhau.
Tứ giác ACA’B có hai đường chéo cắt nhau tại trung điểm mỗi đường
⇒ ACA’B là hình bình hành.
Lại có hai đường chéo AA’; BC vuông góc với nhau nên ACA’B là hình thoi.
⇒ B sai
Chọn B.
C. Bài tập vận dụng
Câu 1: Tìm điểm A’ đối xứng với điểm A( 3;-4) qua đường thẳng d:
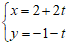
A. ( 4; -2) B. (5; 0) C. ( -1; 2) D. ( -1; -3)
Lời giải:
Đáp án: B
Trả lời:
+ Trước tiên ta tìm hình chiếu của A lên d.
Gọi điểm H(2 + 2t; -1 - t) thuộc d là hình chiếu của A.
Ta có AH→( 2t - 1; 3 - t).
Vectơ chỉ phương của d là u→( 2; -1)
+Do H là hình chiếu của A trên d nên AH vuông góc với d
⇔ u→ . AH→ = 0 ⇔ 2( 2t - 1) – 1( 3 - t) = 0
⇔ 4t- 2- 3+ t= 0 ⇔ t= 1
⇒ H( 4; -2)
Vậy hình chiếu của A trên d là H( 4; -2).
+ Do A’ đối xứng với A qua d nên H là trung điểm của AA’.
⇒ Tọa độ điểm A’ là: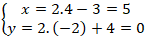 
Câu 2: Cho đường thẳng ∆: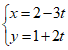 
. Hoành độ điểm M’ đối xứng với M( 4; 5) qua ∆ gần nhất với số nào sau đây ?
A. 1,12 B. - 0, 91 C. 1,31 D. - 0,92
Lời giải:
Đáp án: D
Trả lời:
+ Ta tìm hình chiếu của M trên ∆.
Gọi H là hình chiếu của M trên ∆.
Ta có: H ∈ ∆ nên H( 2 - 3t; 1 + 2t) và MH→( -2 - 3t; -4 + 2t)
Đường thẳng ∆có vectơ chỉ phương là u→(3; - 2) .
MH→ ⊥ u→ ⇔ MH→ . u→ = 0 ⇔ 3(-2 - 3t) - 2(-4 + 2t) = 0 ⇔ -13t + 2 = 0 ⇔ t =
⇒ 
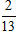
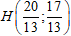
+ Ta tìm điểm M’ đối xứng với M qua ∆.
Ta có H là hình chiếu của M trên ∆ trên M là trung điểm của MM’. Suy ra tọa độ điểm M’ là:
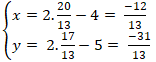
⇒ Hoành độ điểm M’ xấp xỉ - 0,92
Câu 3: Tìm điểm M’ đối xứng với M(4; 1) qua đường thẳng d: x - 2y + 4 = 0 là:
A. (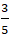
; 
)
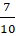
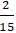
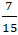
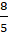
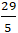
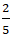
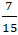
B. (
; 
)
C. (
; 
)
D. (
;
)
Lời giải:
Đáp án: C
Trả lời:
Đường thẳng d có 1 VTPT n→( 1; -2).
+ Ta tìm hình chiếu của M trên d.
Gọi H( 2t - 4; t) là hình chiếu của M( 4; 1) trên đường thẳng d.
Suy ra MH vuông góc d nên hai vecto MH→(2t – 8; t- 1) và n→(1; -2) cùng phương.
Do đó: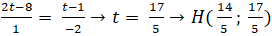 
+ Điểm M’ đối xứng với M qua d nên H là trung điểm của MM’. Suy ra tọa độ điểm M’ là:
⇒ M’(
;
)
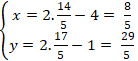
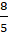
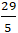
Câu 4: Cho tam giác ABC có A(1; 3).Gọi I(2; 1) là trung điểm của AB và J( -1; 0) là trung điểm của AC. Tìm điểm K đối xứng với điểm A qua IJ?
A. K(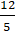
; - 
)
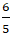
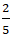
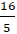
B. K(
;
)
C. K( -
; -
)
D. K(
; 
)
Lời giải:
Đáp án: A
Trả lời:
+ Do I và J lần lượt là trung điểm của AB và AC nên IJ là đường trung bình của tam giác ABC ⇒ IJ// BC ( 1) .
+Gọi H là hình chiếu của A lên IJ
⇒ AH vuông góc IJ .
+ Lập phương trình AH: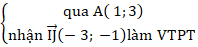 
⇒ ( AH): - 3( x - 1) – 1( y - 3) = 0 hay 3x + y - 6 = 0.
+ Phương trình IJ: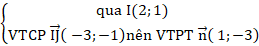 
⇒ Phương trình IJ: 1( x - 2) – 3( y - 1) = 0 hay x - 3y + 1 = 0.
+ Giao điểm của IJ và AH là H. Tọa độ điểm H là nghiệm hệ :
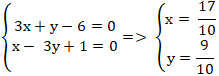
+ Gọi điểm K đối xứng với A qua IJ. Khi đó; H là trung điểm của AK
⇒ Tọa độ điểm K: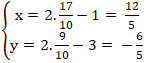 
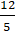
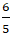
⇒ K(
; -
)
Câu 5: Cho điểm M(- 2; 1) và đường thẳng ∆: 2x - y + 4 = 0.Gọi điểm M’ đối xứng với M qua đường thẳng ∆. Khi đó điểm M’ nằm trên đường thẳng nào?
A. x + 2y - 3 = 0 B. 2x + 4y - 3 = 0 C. x + 2y = 0 D. x + 2y - 6 = 0
Lời giải:
Đáp án: C
Trả lời:
+ Đường thẳng ∆ có 1 VTPT n→( 2; -1)
Gọi H( t; 2t + 4) là hình chiếu của M trên đường thẳng ∆ thì MH→( t + 2; 2t + 3)
⇒ Hai đường thẳng MH và ∆ vuông góc với nhau nên hai vecto MH→ và n→( 2; -1) cùng phương. Suy ra: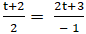 
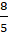
⇔ - t - 2 = 4t + 6 ⇔ t = -
⇒ Tọa độ điểm H( -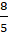
; 
) .
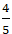
+ Do điểm M’ đối xứng với M qua ∆ nên H là trung điểm của MM’. Suy ra tọa độ điểm M’:
⇒ M’(-
;
)
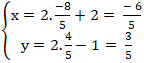
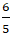
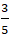
⇒ điểm M’thuộc đường thẳng: x + 2y = 0
Câu 6: Cho đường thẳng ∆: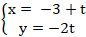 
và điểm M(2; -3); điểm A(-0,6; -1,8). Gọi M’ là điểm đối xứng với M qua đường thẳng ∆. Tính độ dài AM’
A. 3 B. 4 C. 5 D. √17
Lời giải:
Đáp án: C
Trả lời:
+ Gọi H là hình chiếu của M trên ∆.
Ta có: H thuộc ∆ nên H( -3 + t ; - 2t) ⇒ MH→( t- 5 ; 3 - 2t)
Đường thẳng có vectơ chỉ phương là u→( 1; -2) .
Do H là hình chiếu vuông góc của M trên ∆ nên hai đường thẳng MH và ∆ vuông góc với nhau
⇒ MH→ . u→ = 0 ⇔ 1(t - 5) – 2( 3 - 2t) = 0
⇔ t - 5 - 6 + 4t = 0 ⇔ 5t = 11 ⇔ t = 2,2
⇒ H (- 0,8; - 4,4) .
+ Điểm M’ đối xứng với điểm M qua đường thẳng ∆ nên H là trung điểm của MM’. Suy ra tọa độ điểm M’:
⇒ M’( -3,6; -5,8).
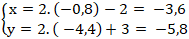
Độ dài đoạn AM’ là:
= 5
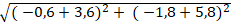
Câu 7: Tìm điểm đối xứng với điểm A( 1; 2) qua đường thẳng d:
= 1
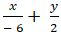
A. H( 1; 2)
B. H( 
; 
)
C. H( -
; 
)
D. H( 
; 
)
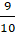
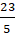
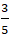
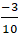
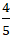
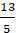
Lời giải:
Đáp án: D
Trả lời:
+ Phương trình tổng quát của đường thẳng d: 2x - 6y + 12 = 0 hay x - 3y + 6 = 0
+ Lấy điểm H(3t - 6; t) thuộc d -là hình chiếu vuông góc của A lên d.
Ta có AH→( 3t - 7; t - 2)
Vectơ pháp tuyến của d là n→( 1; -3) .
+Do H là hình chiếu của A trên d nên hai vecto AH→ và n→ cùng phương :
⇔ 
⇔ - 3( 3t - 7) = 1( t - 2)
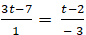
⇔ - 9t + 21 = t - 2 ⇔ t =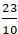 
+ Với t =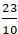
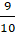
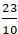
ta có H(
;
)
+ Gọi điểm A’ đối xứng với điểm A qua đường thẳng d. Suy ra H là trung điểm của AA’.
⇒ Tọa độ điểm A’: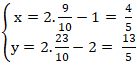 
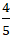
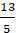
⇒ M’(
;
)
Câu 8: Cho tam giác ABC có AB = 1; BC = 1√2 và góc B = 450.Gọi A’ là điểm đối xứng với A qua BC. Tìm mệnh đề sai?
A. Tứ giác ACA’B là vuông
B. AA’ = 2
C. BA’ = 1
D. Tứ giác ACA’B là hình bình hành
Lời giải:
Đáp án: B
Trả lời:
+ Áp dụng định lí cosin vào tam giác ABC ta có:
AC2 = AB2 + BC2 – 2.AC.BC.Cos B
= 12 + (1√2)2 - 2.1.1√2.cos450 = 1
⇒ AC = 1 nên AB = AC = 1 và AB2 + AC2 = BC2
⇒ Tam giác ABC vuông cân tại A.
+ Gọi H là chân đường cao hạ từ điểm A lên BC.
⇒ AH là đường cao nên đồng thời là đường trung tuyến
⇒ H là trung điểm của BC: AH = BH = CH =
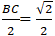
⇒ AA’= √2
+ Do A’ đối xứng với điểm A qua BC nên H là trung điểm của AA’ và AA’; BC vuông góc với nhau.
Tứ giác ACA’B có hai đường chéo cắt nhau tại trung điểm mỗi đường
⇒ ACA’B là hình bình hành.
Lại có hai đường chéo AA’; BC vuông góc với nhau nên ACA’B là hình thoi.
Tam giác ABC vuông cân nên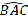 
= 900
⇒ Tứ giác ACA’B là hình vuông.
⇒ B sai
