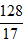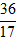Tìm điểm thuộc đường thẳng thỏa mãn điều kiện cho trước - Toán lớp 10
Tìm điểm thuộc đường thẳng thỏa mãn điều kiện cho trước
Với Tìm điểm thuộc đường thẳng thỏa mãn điều kiện cho trước Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm điểm thuộc đường thẳng thỏa mãn điều kiện cho trước từ đó đạt điểm cao trong bài thi môn Toán lớp 10.
A. Phương pháp giải
Muốn tìm tọa độ điểm A thỏa mãn điều kiện T có 2 hướng:
Hướng 1: Tìm hai đường thẳng d và ∆ cùng đi qua điểm A. Khi đó; tọa độ A là nghiệm hệ phương trình :
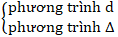
Hướng 2: Nếu điểm A thuộc đường thẳng d: ax + by + c = 0 cho trước và cách điểm B một khoảng là h
⇒ 
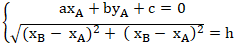
Giải hệ phương trình ta được tọa độ điểm A.
Chú ý: Tính chất các đường trung tuyến; đường cao.. của tam giác. Tính chất các đường chéo của hình bình hành; hình thoi...
B. Ví dụ minh họa
Ví dụ 1. Tam giác ABC có đỉnh A(-1; -3) . Phương trình đường cao BB’:
5x + 3y - 25 = 0; phương trình đường cao
CC’: 3x + 8y - 12 = 0. Toạ độ đỉnh B là
A. (5; 2) B. (2; 5) C. ( 2; -5) D. (-5; 2)
Lời giải
+ Đường thẳng AB vuông góc với CC’ nên nhận u→(3; 8) làm VTCP và n→(8; -3) làm VTPT.
+ Do đó d có phương trình: 8( x + 1) - 3( y + 3) = 0 hay 8x - 3y - 1 = 0
+ Hai đường thẳng BB’ và BC cắt nhau tại B nên tọa độ điểm B là nghiệm của hệ phương trình:
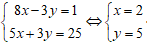
Chọn B.
Ví dụ 2. Cho A( -2; 5) và B(2 ; 3). Đường thẳng d: x - 4y + 4 = 0 cắt AB tại M. Toạ độ điểm M là:
A. (8; 3) B. (0; 1) C. (4; 2) D. (4; -2)
Lời giải:
+ Viết phương trình đường thẳng đi qua 2 điểm A và B: đi qua A( -2; 5), vectơ chỉ phương AB→ = (4; -2) nên vectơ pháp tuyến n→ = (2; 4)
⇒ Phương trình: AB. 2( x + 2) + 4( y - 5) = 0 hay 2x + 4y - 16 = 0
+ Gọi M là giao điểm của 2 đường thẳng AB và đường thẳng d. Tọa độ M thỏa mãn hệ
⇒ M(4; 2)
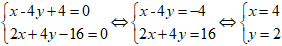
Chọn C.
Ví dụ 3 : Cho tam giác ABC có A(1; -2) , đường cao CH: x - y + 1 = 0, đường phân giác trong BN: 2x + y + 5 = 0. Tọa độ điểm B là
A. ( 4 ; 3) B. ( 4 ; -3) C. (-4 ; 3) D. ( -4 ; -3)
Lời giải
Ta cón đường thẳng AB :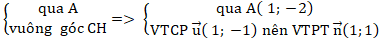 
⇒ ( AB) : 1( x - 1) + 1(y + 2) = 0 hay x + y + 1 = 0
Mà AB và BN cắt nhau tại B nên toạ độ B là nghiệm hệ phương trình .
⇒ B( - 4; 3)
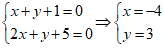
Chọn C.
Ví dụ 4 : Cho tam giác ABC vuông tại A có A(-1 ; 4) ; B( 1 ; -4) và đường thẳng BC đi qua điểm
K(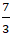 
; 2) . Tìm tọa độ điểm C ?
A. ( 1 ; -2) B. ( -2 ; 3) C. ( 3 ; 5) D. ( -2 ; -1)
Lời giải
+ Phương trình ( BK) :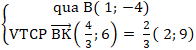 
⇒ Phương trình BK :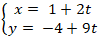 
+ Điểm C thuộc BK nên C( 1 + 2t ; - 4 + 9t) .
+ ta có : AB→( 2; -8); AC→( 2t + 2; 9t - 8)
Do tam giác ABC vuông tại A nên AB→. AC→ = 0
⇒ 2( 2t + 2) – 8( 9t - 8) = 0 ⇔ 4t + 4 - 72t + 64 = 0
⇔ t= 1 ⇒ C( 3 ; 5)
Chọn C.
Ví dụ 5: Cho đường thẳng d: x - y + 2 = 0 và hai điểm A( 0; 4) ; B( 4; -8) . Tìm điểm C thuộc đường thẳng d sao cho C cách đều hai điểm A và B?
A. ( -7; -5) B. ( 1; -4) C. ( -2; -5) D. ( 4; 7)
Lời giải
+ Do điểm C cách đều hai điểm A và B nên C thuộc đường thẳng ∆: đường trung trực của AB.
+ Trung điểm của AB là I ( 2; - 2) .
Đường thẳng ∆: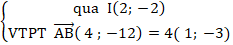 
⇒ Phương trình ∆: 1( x - 2) – 3( y + 2) = 0 hay x - 3y - 8 = 0.
+ Hai đường thẳng d và ∆ cắt nhau tại C nên tọa độ điểm C là nghiệm hệ:
⇒ C( -7; -5)
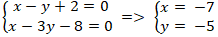
Chọn A.
Ví dụ 6: Cho tam giác ABC biết AB: x + y - 1 = 0; AC: x - y + 3 = 0 và trọng tâm
G(1; 2). Tìm tọa độ điểm B?
A. ( -2; 1) B. ( 2 ; -1) C. ( 3; 2) D. ( 1; -3)
Lời giải
+ Hai đường thẳng AB và AC cắt nhau tại A nên tọa độ điểm A là nghiệm hệ
⇒ A( -1; 2).
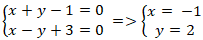
+ Điểm B( a; 1 - a) thuộc đường thẳng AB và điểm C( b; b + 3) thuộc đường thẳng AC.
+ Do G( 1; 2) là trọng tâm tam giác nên ta có:
⇔ a = b = 2
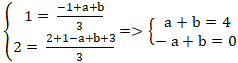
⇒ Điểm B( 2; - 1) và C( 2; 5)
Chọn B.
Ví dụ 7. Cho hình chữ nhật ABCD có phương trình của AB: 2x - y + 5 = 0, đường thẳng AD qua gốc tọa độ O , và tâm hình chữ nhật là I( 4; 5 ). Tìm tọa độ điểm D.
A. D(22; 11)
B. D(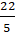 
; 
)
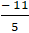
C. D( 3 ; - 5)
D. D( 4; 8)
Lời giải
+ Đường thẳng AD: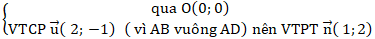 
⇒ Phương trình AD: 1( x - 0) + 2( y - 0) = 0 hay x + 2y = 0.
+ Hai đường thẳng AB và AD cắt nhau tại A nên tọa độ A là nghiệm hệ :
⇒ A ( -2; 1) .
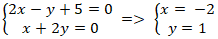
+ Do I là tâm hình chữ nhật nên I là trung điểm AC.
⇒ Tọa độ C( 10; 9) .
+ Đường thẳng CD // AB nên có dạng ( CD) : 2x - y + c = 0 ( c ≠ 5) .
Mà C( 10; 9) thuộc CD nên 2.10 - 9 + c = 0 ⇒ c = - 11
Vậy phương trình CD: 2x - y - 11 = 0.
+ Hai đường thẳng AD và CD cắt nhau tại D nên tọa độ D là nghiệm hệ :
⇒ D(
;
)
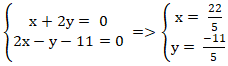
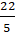
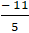
Chọn B.
Ví dụ 8: Cho tam giác ABC có AB = 1; BC = 1√2 và góc B = 450.Gọi A’ là điểm đối xứng với A( 2; 0) qua BC; M( -1; 1) là trung điểm của BC. Tìm tọa độ điểm A’?
A. ( 1; 0) B. ( -4; 2) C. ( 1; 1) D. Không đủ dữ liệu
Lời giải
+ Áp dụng định lí cosin vào tam giác ABC ta có:
AC2 = AB2 + BC2 – 2.AC.BC.CosB
= 12 + (1√2)2 - 2.1.1√2.cos450 = 1
⇒ AC = 1 nên AB = AC = 1 và AB2 + AC2 = BC2
⇒ Tam giác ABC vuông cân tại A.
⇒ AM là đường trung tuyến nên đồng thời là đường cao.
+ Do A’ đối xứng với điểm A qua BC nên M là trung điểm của AA’.
⇒ Tọa độ của A’ là: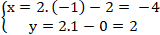 
⇒ A’( - 4; 2)
Chọn B.
C. Bài tập vận dụng
Câu 1: Cho tam giác ABC có trung điểm của AB là I( 1; 3) , trung điểm AC là J( -3; 1). Điểm A thuộc Oy và đường BC qua gốc tọa độ O . Tìm tọa độ điểm A ?
A. ( 0; 1) B. (0; -2) C. (0; 5) D. (0; 8)
Lời giải:
Đáp án: C
Trả lời:
+ Phương trình IJ: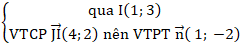 
⇒ Phương trình IJ: 1( x - 1) – 2( y - 3) = 0 hay x - 2y + 5 = 0.
+ Do I và J lần lượt là trung điểm của AB và CA nên IJ là đường trung bình của tam giác ABC. Suy ra: IJ// BC
+ Đường thẳng IJ// BC nên BC có dạng: x - 2y + c = 0 (c ≠ 5) .
Do BC qua O nên : 0 - 2. 0 + c = 0 ⇔ c = 0
Vậy phương trình BC: x - 2y = 0.
+ Điểm A( 0; a) thuộc trục Oy.
Do J ( - 3; 1) là trung điểm của AC nên C( - 6; 2 - a).
Mà điểm C thuộc BC nên : - 6 - 2( 2 - a) = 0 ⇔ a = 5.
Vậy tọa độ điểm A( 0; 5) .
Câu 2: Cho đường thẳng ∆: x + y - 3 = 0. Tìm tọa độ điểm A thuộc ∆ và cách gốc tọa độ một khoảng bằng √17?
A. ( 4; -1) B. ( -1; 4) C. ( 2; 1) hoặc ( -2; 5) D. Cả A và B đúng
Lời giải:
Đáp án: D
Trả lời:
+ Gọi điểm A( a; b) .
Do điểm A thuộc đường thẳng ∆ nên a + b - 3 = 0. ( 1)
+ Khoảng cách từ điểm A đến điểm O là:
AO =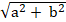 
= √17 ⇔ a2 + b2 = 17 (2)
Từ ( 1) suy ra: a = 3 - b thay vào ( 2) ta được:
( 3-b)2 + b2 = 17 ⇔ 2b2 - 6b - 8 = 0
⇔ b = - 1 hoặc b = 4.
Với b = - 1 ⇒ a = 4 ⇒ A( 4; -1)
Với b = 4 ⇒ a = - 1 ⇒ A( -1; 4) .
Vậy có hai điểm thỏa mãn là A( 4; -1) và A( -1; 4) .
Câu 3: Cho tam giác ABC có đỉnh A(2; 1) , đường cao BH có phương trình x - 3y - 7 = 0 và đường trung tuyến CM có phương trình x + y + 1 = 0. Xác định toạ độ các đỉnh B
A. (-2; -3) B. (1; -2) C. (4; - 1) D. (6; 3)
Lời giải:
Đáp án: A
Trả lời:
+ Điểm M ( m; - m - 1) thuộc đường thẳng CM.
+ Do M là trung điểm của AB nên tọa độ điểm B là:
⇒ B( 2m - 2; - 2m - 3)
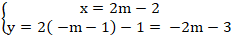
+ Điểm B thuộc đường thẳng BH nên ta có:
2m - 2 - 3(-2m - 3) – 7= 0 ⇔ 2m - 2 + 6m + 9 - 7 = 0
⇔ 8m = 0 ⇔ m = 0
⇒ Tọa độ điểm B( -2; - 3) .
Câu 4: Phương phương trình các cạnh của tam giác ABC biết đỉnh C(4 ; -1) ; đường cao và đường trung
tuyến xuất phát từ A có phương trình (d1): 2x - 3y + 12 = 0 và
(d2): 2x + 3y = 0. Tìm tọa độ điểm B ?
A. ( 4 ; -6) B. ( 8 ; -7) C. (4 ; 2) D. (-4 ; -9)
Lời giải:
Đáp án: B
Trả lời:
+ Hai đường thẳng (d1) và (d2) cắt nhau tại A nên tọa độ A là nghiệm hệ :
⇒ A(-3 ; 2).
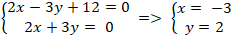
+ Đường thẳng BC :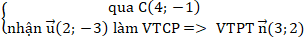 
( vì BC vuông d1).
⇒ Phương trình BC : 3(x - 4)+ 2( y + 1) = 0 hay 3x + 2y - 10 = 0.
+ Hai đường thẳng BC và (d2) cắt nhau tại trung điểm M của BC nên tọa độ M là nghiệm hệ :
⇒ M( 6 ; -4).
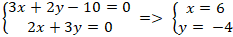
+ Do M là trung điểm của BC nên tọa độ điểm B là :
⇒ B( 8 ; -7)
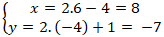
Câu 5: Cho hình thoi ABCD có tâm I. Đường thẳng AC có phương trình : 2x + y - 5 = 0. Biết đường thẳng BD đi qua gôc tọa độ O. Tìm tọa độ điểm I ?
A. (-2 ; -1) B. (1 ; 3) C. (2 ; 1) D. (-3 ; 0)
Lời giải:
Đáp án: C
Trả lời:
+ Đường thẳng BD : 
⇒ Phương trình BD : 1(x - 0) – 2(y - 0) = 0 hay x - 2y = 0.
+ Hai đường thẳng AC và BD cắt nhạu tại I nên tọa độ I là nghiệm hệ :
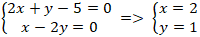
Vậy tọa độ điểm I(2 ; 1).
Câu 6: Cho hình thoi ABCD có điểm A( 1 ; 0) ; phương trình cạnh BC : x + 7y - 7 = 0 và phương trình BD : x + 2y + 9 = 0. Tìm tọa độ điểm D ?
A. (-1 ; 7) B. (-9 ; 0) C. (1 ; -5) D. ( -13 ; 2)
Lời giải:
Đáp án: D
Trả lời:
+ Đường thẳng AD// BC : x + 7y - 7 = 0 nên đường thẳng AD có dạng :
x + 7y + c = 0 ( c ≠ -7) .
Mà điểm A thuộc AD nên : 1 + 7.0 + c = 0 ⇔ c = -1
⇒ Phương trình AD : x + 7y - 1 = 0.
+ Hai đường thẳng AD và BD cắt nhau tại D nên tọa độ D là nghiệm hệ :
⇒ D( -13 ; 2)
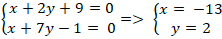
Câu 7: Trên đường thẳng ( d) : x + 2y - 5 = 0. Tìm điểm M cách đều hai điểm A( 2 ; -3) và B ( -1 ; 2) ?
A. ( -2 ; 1) B. (3 ;1) C. (-2 ; -4) D. Đáp án khác
Lời giải:
Đáp án: B
Trả lời:
Gọi tọa độ điểm M(a ; b) .
+ Điểm M thuộc đường thẳng d nên a + 2b - 5 = 0. ( 1)
+ Độ dài : MA =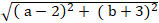 
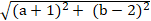
; MB = 
+ Do M cách đều hai điểm A và B nên MA= MB
⇔ MA2 = MB2 ⇔ ( a - 2)2 + (b + 3)2 = (a + 1)2 + (b - 2)2
⇔ a2 – 4a + 4 + b2 + 6b + 9 = a2 + 2a + 1 + b2 – 4b + 4
⇔ - 6a + 10b + 8 = 0 ( 2)
+ Từ ( 1) và ( 2) có hệ phương trình :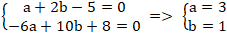 
Vậy tọa độ điểm M( 3; 1)
Câu 8: Cho tam giác ABC có A( 1 ; -2) ; B( -2 ; 0). Có bao nhiêu điểm C để tam giác ABC vuông cân tại C ?
A. 1 B. 2 C. 0 D. 3
Lời giải:
Đáp án: B
Trả lời:
+ Gọi tọa độ điểm C( a ; b).
⇒ AC→(a - 1; b + 2); BC→( a + 2; b)
AC =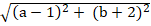 
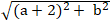
; BC = 
+ Để tam giác ABC vuông cân tại C thì :
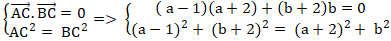
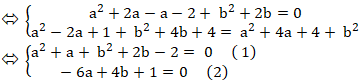
+ Từ (2) suy ra : b =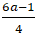 
thay vào ( 1) ta được :
a2 + a + (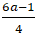
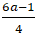
)2 + 2.
- 2 = 0
⇔ a2 + a +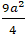 
- 
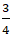
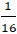
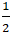
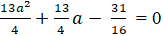
a + 
+ 3a - 
- 2 = 0
⇔ 
Phương trình trên có hai nghiệm phân biệt nên có hai điểm C thỏa mãn bài toán.
Câu 9: Tam giác ABC đều có A(-1; -3) và đường cao BB’: 5x + 3y - 15 = 0. Tọa độ đỉnh C là:
A. C(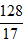
; 
)
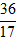
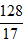
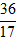
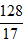
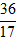
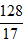
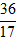
B. C( -
; -
)
C. C(
; -
)
D. C(-
;
)
Lời giải:
Đáp án: A
Trả lời:
+ Vì tam giác ABC đều nên A và C đối xứng nhau qua BB’.
+ Gọi d là đường thẳng qua A và d ⊥ BB' ⇒ d: 3x - 5y - 12 = 0
H = d ∩ BB' ⇒ tọa độ điểm H là nghiệm của hệ:
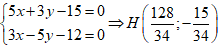
H là trung điểm AC suy ra C(
;
)
