Viết phương trình đường thẳng thỏa mãn điều kiện cho trước - Toán lớp 10
Viết phương trình đường thẳng thỏa mãn điều kiện cho trước
Với Viết phương trình đường thẳng thỏa mãn điều kiện cho trước Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập phương trình đường thẳng thỏa mãn điều kiện cho trước từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải
- Để viết được phương trình đường thẳng d cần xác định được hai yếu tố:
+ Một điểm A thuộc đường thẳng d.
+ Một VTPT hoặc một VTCP của đường thẳng.
- Hai đương thẳng vuông góc với nhau thì VTCP của đường thẳng này là VTPT của đường thẳng kia.
- Hai đường thẳng song song có cùng VTPT; VTCP.
- Nhớ đến các tính chất của hình vuông; hình chữ nhật ; hình thoi...đường trung bình của tam giác...
B. Ví dụ minh họa
Ví dụ 1: Cho tam giác ABC có M ( 1; 3) ; N( 3; -1) và P( -1; 5) lần lượt là trung điểm của AB; BC; AC. Viết phương trình AB.
A. 2x + 3y - 1 = 0 B. 2x - 3y + 3 = 0 C. 3x + 2y - 9 = 0 D. 2x - 3y + 1 = 0
Lời giải
Do N và P lần lượt là trung điểm của BC và AC nên NP là đường trung bình của tam giác ABC.
⇒ NP// AB.
Đường thẳng AB: 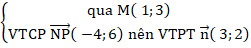
⇒ Phương trình AB: 3( x - 1) + 2( y - 3) = 0 hay 3x + 2y – 9 = 0
Chọn C.
Ví dụ 2: Cho hình bình hành ABCD, biết A( -2; 1) và phương trình đường thẳng CD là 3x - 4y - 5 = 0. Phương trình tham số của đường thẳng AB là:
A. 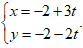
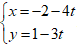
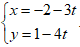
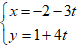
Lời giải
Vì ABCD là hình bình hành nên AB//CD.
Do đó đường thẳng AB: đi qua A (-2; 1) và nhận vtpt của CD là (3; -4) làm vtpt.
⇒ đường thẳng AB có vtcp (-4; -3) nên phương trình tham số của đường thẳng AB là
Chọn B.
Ví dụ 3: Gọi H là trực tâm của tam giác ABC. Phương trình các cạnh và đường cao của tam giác là: AB: 7x - y + 4 = 0, BH: 2x + y - 4 = 0 và AH: x - y - 2 = 0. Phương trình đường cao CH của tam giác ABC là:
A. 7x + y - 2 = 0 B. 7x - y = 0 C. x - 7y - 2 = 0 D. x + 7y - 2 = 0
Lời giải
+ Ta có BH và CH cắt nhau tại H nên tọa độ H là nghiệm của hệ phương trình
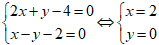
+ Ta có H là trực tâm tam giác ABC nên CH vuông góc AB.
⇒ CH nhận VTPT của AB làm VTCP.
⇒ Đường thẳng CH : 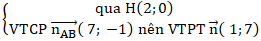
⇒ Phương trình đường thẳng CH :
1( x - 2) + 7( y - 0) = 0 hay x + 7y - 2 = 0
Chọn D
Ví dụ 4 : Cho tam giác ABC biết trực tâm H(1; 1) và phương trình cạnh
AB: 5x - 2y + 6 = 0, phương trình cạnh AC: 4x + 7y - 21 = 0 . Phương trình cạnh BC là
A. 4x - 2y + 1 = 0 B. x - 2y + 14 = 0 C. x + 2y - 14 = 0 D. x - 2y - 14 = 0
Lời giải
+ Ta có AB và AC cắt nhau tại A nên tọa độ điểm A là nghiệm hệ :
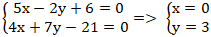
+ Do BH vuông góc AC nên đường thẳng BH nhận nAC→( 4;7) làm VTCP
⇒ một VTPT của AC: ( 7; -4) .
Đường thẳng BH: 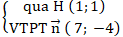
⇒ Phương trình BH: 7( x - 1) – 4( y - 1) = 0 hay 7x - 4y - 3 = 0
+ Do AB và BH cắt nhau tại B nên tọa độ B là nghiệm hệ:
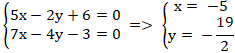
+ Phương trình ( BC) : 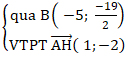
Suy ra (BC): (x + 5) - 2(y + 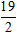
Chọn D.

Ví dụ 5 : Cho tam giác ABC có A(4; -2). Đường cao BH: 2x + y - 4 = 0 và đường cao CK: x - y - 3 = 0. Viết phương trình đường cao kẻ từ đỉnh A.
A. 4x + 5y - 6 = 0 B. 4x - 5y - 26 = 0 C. 4x + 3y - 10 = 0 D. 4x - 3y - 22 = 0
Lời giải
Gọi AI là đường cao kẻ từ đỉnh A.
Gọi H1 là trực tâm của tam giác ABC, khi đó tọa độ điểm H1 thỏa mãn hệ phương trình
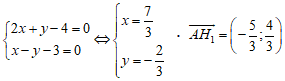
+ Đường cao AI qua H1(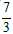
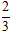
⇒ AI: 4(x - 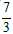
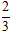
Chọn A.
Ví dụ 6: Cho hình bình hành ABCD có phương trình các cạnh AB : x + 3y - 4 = 0 và AC: 2x - 3y + 1 = 0. Hai đường chéo AC và BD cắt nhau tại I( 2; -3). Viết phương trình cạnh CD?
A. x + 3y + 18 = 0 B. x + 3y - 17 = 0 C. x + 3y - 6 = 0 D. x + 3y - 2 = 0
Lời giải
+ Hai đường thẳng AB và AC cắt nhau tại A nên tọa độ điểm A là nghiệm hệ phương trình :
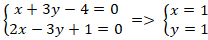
+ Do ABCD là hình bình hành nên hai đường chéo cắt nhau tại trung điểm mỗi đường
⇒ I là trung điểm của AC.
⇒ Tọa độ điểm C(3; -7).
+ Đường thẳng CD// AB nên phương trình đường thẳng CD có dạng:
x + 3y + c = 0 ( c khác -4)
Lại có điểm C( 3; -7) thuộc CD nên: 3 + 3.(-7) + c = 0 ⇔ c = 18.
Vậy phương trình CD: x + 3y + 18 = 0.
Chọn A
Ví dụ 7: Cho tam giác ABC có B( 3; 5) ; đường cao và đường trung tuyến kẻ từ A có phương trình ( AH) 2x - 5y + 4 = 0 và ( AM) x + y - 5 = 0. Viết phương trình cạnh AB?
A. 11x + 5y - 43 = 0 B. 2x – 5y + 1 = 0 C. 10x - y + 19 = 0 D. 4x - 7y + 19 = 0
Lời giải
+ Đường cao và đường trung tuyến kẻ từ A cắt nhau tại A nên tọa độ điểm A là nghiệm hệ :
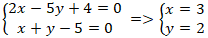
+ Phương trình BC:
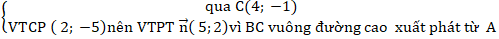
⇒ Phương trình BC: 5( x - 4) + 2(y + 1) = 0 hay 5x + 2y - 18 = 0
+ Đường trung tuyến AM và BC cắt nhau tại trung điểm M của BC nên tọa độ điểm M:
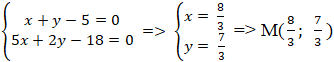
+ M là trung điểm BC nên tọa độ điểm B(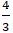
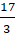
+ Đường thẳng AB: 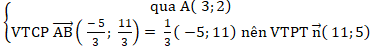
⇒ Phương trình AB: 11( x - 3) + 5( y - 2) = 0 hay 11x + 5y - 43 = 0
Chọn A.
Ví dụ 8: Cho tam giác ABC vuông tại C biết 2 điểm A( -1; 2) và B( 3; 4) và
C( 2m - 1; m). Viết phương trình đường trung tuyến CM?
A. x + 2y - 7 = 0 B. 13x – 14y + 29 = 0 C. Cả A và B đúng D. Đáp án khác
Lời giải
+ Gọi M là trung điểm của AB; tọa độ điểm M là:
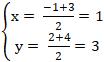
+ Ta có: AC→( 2m; m - 2); BC→( 2m - 4 ;m - 4)
Do tam giác ABC vuông tại C nên AC→ . BC→ = 0
⇔ 2m( 2m - 4) – (m - 2) ( m - 4) = 0
⇔ 4m2 – 8m - m2 + 4m + 2m - 8 = 0
⇔ 3m2 – 2m - 8 = 0 ⇔ m = 2 hoặc m = 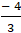
+ Với m = 2 thì C( 3; 2)
Đường trung tuyến CM: 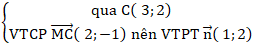
⇒ Phương trình CM: 1( x - 3) + 2( y - 2) = 0 hay x + 2y - 7 = 0
+ Với m= 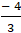
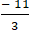
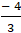
Đường trung tuyến AM: 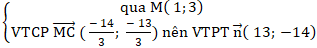
⇒ Phương trình CM: 13(x - 1) - 14( y - 3) = 0 hay 13x – 14y + 29 = 0 .
Chọn C.

C. Bài tập vận dụng
Câu 1: Cho tam giác ABC có B(0; -3); C( 1; -2); phương trình đường cao BH:
x - 2y + 3 = 0 và
đường trung tuyến AM: x + y - 2 = 0. Viết phương trình đường thẳng AB?
A. 2x - 3y + 9 = 0 B. 7x + 2y + 6 = 0 C. 5x - 4y + 2 = 0 D. Tất cả sai
Lời giải:
Đáp án: B
Trả lời:
+ Đường thẳng AC:
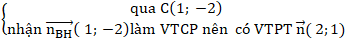
⇒ Phương trình AC: 2(x - 1)+ 1( y + 2) = 0 hay 2x + y = 0
+ Hai đường thẳng AC và AM cắt nhau tại A nên tọa độ điểm A là nghiệm hệ:
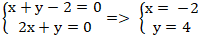
+ Đường thẳng AB: 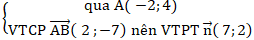
⇒ Phương trình AB: 7( x + 2) + 2(y - 4) = 0 hay 7x + 2y + 6 = 0
Câu 2: Cho hình thoi ABCD và AC cắt BD tại I( 2; 3). Phương trình AB: 2x - y + 4 = 0 và BC: x + y + 2 = 0. Viêt phương trình AC?
A. 4x + 3y - 17 = 0 B. 2x + 3y - 9 = 0 C. 3x - 4y + 1 = 0 D. x + 5y - 6 = 0
Lời giải:
Đáp án: A
Trả lời:
+ Hai đường thẳng AB và BC cắt nhau tại B nên tọa độ điểm B là nghiệm hệ :
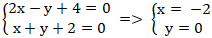
+ Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau.
⇒ Đường thẳng AC: 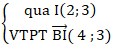
⇒ PHương trình AC: 4(x - 2) + 3(y - 3) = 0 hay 4x + 3y - 17 = 0
Câu 3: Cho tam giác ABC cân tại A có đường cao CK: x + 3y - 6 = 0; đường phân giác AM: x + y - 4 = 0 biết điểm B( 1; 0) . Viết phương trình đường cao xuất phát từ đỉnh B?
A. 2x + y - 2 = 0 B. 2x + y- 7 = 0 C. x - 3y + 9 = 0 D. 7x - y - 7 = 0
Lời giải:
Đáp án: B
Trả lời:
+ Do tam giác ABC cân tại A nên đường phân giác AM đồng thời là đường cao.
+ Tam giác ABC có hai đường cao AM và CK. Gọi giao điểm hai đường cao là H.
⇒ H là trực tâm tam giác và tọa độ điểm H là nghiệm hệ phương trình :
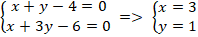
+ Đường cao xuất phát từ đỉnh B chính là đường thẳng BH.
Đường thẳng BH: 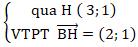
⇒ Phương trình BH: 2( x - 3) + 1(y - 1) = 0 hay 2x + y - 7 = 0
Câu 4: Cho hình vuông ABCD có phương trình AB: x - y + 6 = 0 và AD: x + y = 0; tọa độ điềm C( 1; -5) . Viết phương trình BD?
A. x + 2y - 3 = 0 B. x + 2y = 0 C. x - 2y + 1 = 0 D. x - 2y - 1 = 0
Lời giải:
Đáp án: D
Trả lời:
+ Hai đường thẳng AB và AD cắt nhau tại A nên tọa độ A là nghiệm hệ”
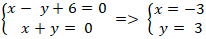
+ Gọi I là trung điểm của AC nên tọa độ điểm I :
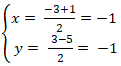
+ Đường thẳng BD: 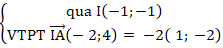
⇒ Phương trình BD: 1( x + 1) - 2( y + 1) = 0 hay x - 2y - 1 = 0

Câu 5: Cho tam giác ABC biết AB: x + y - 1 = 0; AC: x - y + 3 = 0 và trọng tâm G(1; 2). Viết phương trình BC?
A. x + 2 = 0 B. y + 1 = 0 C. 2x + 3y - 1 = 0 D. -x + 3y - 1 = 0
Lời giải:
Đáp án: B
Trả lời:
+ Hai đường thẳng AB và AC cắt nhau tại A nên tọa độ điểm A là nghiệm hệ
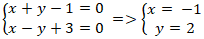
+ Điểm B( a; 1 - a) thuộc đường thẳng AB và điểm C( b; b + 3) thuộc đường thẳng AC.
+ Do G( 1; 2) là trọng tâm tam giác nên ta có:
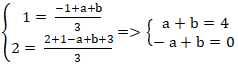
⇒ Điểm B( 2; -1) và C( 2; 5) .
+ Đường thẳng BC: 
⇒ Phương trình BC: 0( x - 2) + 1( y + 1) = 0 hay y + 1 = 0
Câu 6: Cho hình chữ nhật ABCD có phương trình của AB: x - 2y + 3 = 0, đường thẳng AD qua gốc tọa độ O , và tâm hình chữ nhật là I( 2; -2 ). Viết phương trình CD?
A. x + 2y - 3 = 0 B. x - 2y - 15 = 0 C. x - 2y + 1 = 0 D. x - 2y + 6 = 0
Lời giải:
Đáp án: B
Trả lời:
+ Đường thẳng AD:
⇒ Phương trình AD: 2( x - 0) + 1( y - 0) = 0 hay 2x + y = 0
+ Hai đường thẳng AB và AD cắt nhau tại A nên tọa độ A là nghiệm hệ :
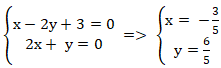
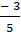
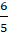
+ Do I là tâm hình chữ nhật nên I là trung điểm AC.
⇒ Tọa độ C( 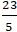
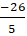
+ Đường thẳng CD // AB nên có dạng ( CD) : x - 2y + c = 0 ( c ≠ 5) .
Mà C thuộc CD nên 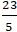
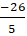
Vậy phương trình CD: x - 2y - 15 = 0.
Câu 7: Cho tam giác ABC có trung điểm của AB là I( 1; 3) , trung điểm AC là J( -3; 1). Điểm A thuộc Oy và đường BC qua gốc tọa độ O . Viết phương trình đường thẳng CI?
A. 3x - 2y + 3 = 0 B. 3x + 2y - 9 = 0 C. 6x - 7y + 15 = 0 D. 5x - 2y + 1 = 0
Lời giải:
Đáp án: C
Trả lời:
+ Phương trình IJ: 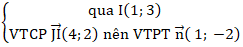
⇒ Phương trình IJ: 1(x - 1) – 2( y - 3) = 0 hay x - 2y + 5 = 0.
+ Do I và J lần lượt là trung điểm của AB và CA nên IJ là đường trung bình của tam giác ABC. Suy ra: IJ// BC
+ Đường thẳng IJ// BC nên BC có dạng: x - 2y + c = 0 (c ≠ 5) .
Do BC qua O nên : 0 - 2.0 + c = 0 ⇔ c = 0
Vậy phương trình BC: x - 2y = 0.
+ Điểm A( 0; a) thuộc trục Oy.
Do J ( - 3; 1) là trung điểm của AC nên C( - 6; 2 - a).
Mà điểm C thuộc BC nên : - 6 - 2( 2 - a) = 0 ⇔ a = 5.
⇒ Tọa độ điểm C( -6; - 3).
+ Đường thẳng CI: 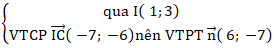
⇒ Phương trình CI: 6(x - 1) – 7(y - 3) = 0 hay 6x - 7y + 15 = 0
Câu 8: Cho tam giác ABC có M; N và P lần lượt là trung điểm của AB; AC và BC. Biết M( 2; -1); N( - 2; -1) và P ( 0; 3).Viết phương trình đường trung trực d của đoạn thẳng BC?
A. x = 0 B. x + y - 3 = 0 C. 2x - y + 3 = 0 D. y - 3 = 0
Lời giải:
Đáp án: C
Trả lời:
+ Do M và N là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC và MN// BC ( 1).
Mà d là đường trung trực của BC nên d vuông góc BC (2).
Từ (1) và (2) suy ra: MN vuông góc d.
+ Đường thẳng d: 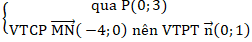
⇒ Phương trình d: 0(x - 0) + 1( y - 3) = 0 hay y - 3 = 0

