Tính độ dài vectơ khi biết tích vectơ với một số (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Tính độ dài vectơ khi biết tích vectơ với một số lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Tính độ dài vectơ khi biết tích vectơ với một số.

Tính độ dài vectơ khi biết tích vectơ với một số (bài tập + lời giải)

1. Phương pháp giải

- Vectơ k$\overrightarrow{a}$(k là số thực khác 0) có độ dài bằng $\left|k\right|.\left|\overrightarrow{a}\right|$.

- Ta quy ước: $0\overrightarrow{a}=\overrightarrow{0}$ và $k\overrightarrow{0}=\overrightarrow{0}$.

- Tính chất: Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bất kì, với mọi số thực h và k, ta có:

+) $k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{a}+k\overrightarrow{b}$;

+) $(h+k)\overrightarrow{a}=h\overrightarrow{a}+k\overrightarrow{a}$;

+) $h\left(k\overrightarrow{a}\right)=\left(hk\right)\overrightarrow{a}$;

+) $1.\overrightarrow{a}=\overrightarrow{a}$;

+) $(-1)\overrightarrow{a}=-\overrightarrow{a}$.

- Sử dụng định nghĩa về độ dài tích của vectơ với một số và các tính chất về phép toán với vectơ, các quy tắc trung điểm, trọng tâm, ... kết hợp với định lí Pythagore, các hệ thức lượng trong tam giác, ... để tính các độ dài.

2. Ví dụ minh họa

Ví dụ 1. Cho tam giác ABC vuông tại A, có M nằm trên cạnh AB, N nằm trên cạnh AC. Biết AB = 6, AC = 8 và $\overrightarrow{MN}=\frac{1}{2}\overrightarrow{BC}$. Tính: $\left|\overrightarrow{MN}\right|$.

Hướng dẫn giải:

Xét  tam giác ABC vuông tại A

Áp dụng định lí Pythagore ta có:

BC² = AB² + AC² = 6² + 8² = 100 ⇔ BC = 10

Ta có: $\overrightarrow{MN}=\frac{1}{2}\overrightarrow{BC}\iff \left|\overrightarrow{MN}\right|=\left|\frac{1}{2}\right|\left|\overrightarrow{BC}\right|=\frac{1}{2}.10=5$

Vậy $\left|\overrightarrow{MN}\right|$ = 5.

Ví dụ 2. Cho đoạn thẳng AB, có M nằm giữa A và B. Biết $\overrightarrow{MA}=-2\overrightarrow{MB}$. Tính độ dài đoạn thẳng AB. Biết MA = 4.

Hướng dẫn giải:

Ta có:

$\overrightarrow{MA}=-2\overrightarrow{MB}\iff \left|\overrightarrow{MA}\right|=\left|-2\right|\left|\overrightarrow{MB}\right|\iff \left|\overrightarrow{MB}\right|=\frac{\left|\overrightarrow{MA}\right|}{2}=\frac{4}{2}=2$

Hay MB = 2

Do M nằm giữa A và B nên ta có: AB = MA + MB = 4 + 2 = 6.

3. Bài tập tự luyện

Bài 1. Cho tam giác đều ABC cạnh 4. Vectơ $-\frac{1}{2}\overrightarrow{BC}$ có độ dài là.

A. 2;

B. 4;

C. 3;

D. 6.

Bài 2. Cho hình vuông ABCD tâm O cạnh 3. Ta có $\left|\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{DB}\right|$= ?

A. 2;

B. 4;

C. 3;

D. 6.

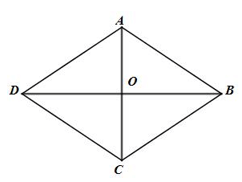
Bài 3. Cho hình thoi ABCD cạnh 5 và $\widehat{ABC}={60}^o$. Tính: $\left|2\overrightarrow{AB}+2\overrightarrow{AD}\right|$.

A. 10;

B. $\frac{5\sqrt{3}}{2}$;

C. 5;

D. $5\sqrt{3}$.

Bài 4. Cho hình thoi ABCD cạnh 5 và $\widehat{ABC}={60}^o$. Tính: $\left|2\overrightarrow{AB}-2\overrightarrow{AD}\right|$.

A. 10;

B. $\frac{5\sqrt{3}}{2}$;

C. 5;

D. $10\sqrt{3}$.

Bài 5. Cho hình chữ nhật ABCD tâm O có AB = 4, AD = 3. Tính độ dài vectơ $\frac{1}{2}\overrightarrow{DB}$.

A. 5;

B. 2,5;

C. 1,5;

D. 2.

Bài 6. Cho tam giác đều ABC cạnh a. Điểm M là trung điểm BC. Tính: $\left|\frac{1}{2}\overrightarrow{CB}+\overrightarrow{MA}\right|$.

A. a;

B. 3a;

C. 2a;

D. 4a.

Bài 7. Cho tam giác đều ABC cạnh a. Tính: $\left|\overrightarrow{BA}-\frac{1}{2}\overrightarrow{BC}\right|$.

A. a;

B. 3a;

C. $\frac{a\sqrt{3}}{2}$ ;

D. $a\sqrt{2}$.

Bài 8. Cho hình thoi ABCD tâm O cạnh a. Ta có $\left|2\overrightarrow{DO}+\overrightarrow{BC}+2\overrightarrow{CO}\right|$= ?

A. a;

B. 3a;

C. $\frac{a\sqrt{3}}{2}$;

D. $a\sqrt{2}$.

Bài 9. Cho hình vuông ABCD tâm O cạnh 2a. Vectơ tổng $2\overrightarrow{AB}+2\overrightarrow{DC}$ có độ dài là

A. a;

B. 8a;

C. 4a;

D. 2a.

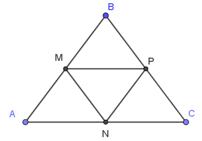
Bài 10. Cho tam giác ABC đều cạnh 4a. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Tính: $\left|\frac{1}{2}\overrightarrow{BA}-\frac{1}{2}\overrightarrow{BC}\right|$.

A. a;

B. 8a;

C. 4a;

D. 2a.