Xác định các điểm thỏa mãn đẳng thức vectơ (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Xác định các điểm thỏa mãn đẳng thức vectơ lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Xác định các điểm thỏa mãn đẳng thức vectơ.

Xác định các điểm thỏa mãn đẳng thức vectơ (bài tập + lời giải)

1. Phương pháp giải

• Để xác định điểm M thỏa mãn một đẳng thức vectơ cho trước, ta biến đổi đẳng thức vectơ cho trước về dạng $\overrightarrow{OM}=\overrightarrow{v}$ , trong đó điểm O và vectơ $\overrightarrow{v}$ đã biết. Khi đó ta xác định được duy nhất điểm M.

• Để xác định tập hợp điểm M thỏa mãn đẳng thức vectơ cho trước, ta có thể biến đổi đẳng thức về một trong các dạng:

+) $\left|\overrightarrow{AM}\right|=R$ (R là hằng số) thì tập hợp điểm M là đường tròn tâm A bán kính R nếu R > 0, là tập rỗng nếu R < 0, M là A nếu R = 0.

+) $\left|\overrightarrow{MA}\right|=k\left|\overrightarrow{BC}\right|$ với A, B, C cho trước thì tập hợp điểm M là đường tròn tâm A, bán kính bằng k.BC.

+) $\left|\overrightarrow{MA}\right|=\left|\overrightarrow{MB}\right|$ với A, B cho trước thì M thuộc đường trung trực của đoạn AB.

+) $\overrightarrow{MA}=k\overrightarrow{BC}$ với A, B, C cho trước thì M là: đường thẳng qua A song song với BC nếu k là số thực; nửa đường thẳng qua A song song với BC theo hướng từ B đến C với k là số thực dương; nửa đường thẳng qua A song song với BC theo hướng từ C đến B với k là số thực âm.

• Chú ý - Ta thường sử dụng các quy tắc sau để biến đổi:

- Quy tắc ba điểm: Với 3 điểm A, B, C ta luôn có $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, $\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}$.

- Quy tắc hình bình hành: Cho hình bình hành ABCD, ta có $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$.

- Quy tắc trung điểm: $\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$ với I là trung điểm của AB.

- Quy tắc trọng tâm: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ với G là trọng tâm của tam giác ABC.

- Sử dụng các tính chất của phép cộng, phép trừ hai vectơ.

2. Ví dụ minh họa.

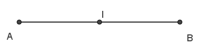
Ví dụ 1. Cho đoạn thẳng AB. Xác định điểm I thỏa mãn: $\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$.

Hướng dẫn giải:

Ta có: $\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$

Do đó, theo quy tắc trung điểm, I là trung điểm của đoạn thẳng AB.

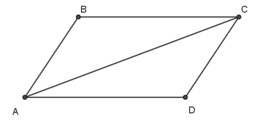
Ví dụ 2. Cho tam giác ABC. Xác định điểm D sao cho: $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$

Hướng dẫn giải:

Theo quy tắc hình bình hành đối với hình bình hành ABCD, ta có: $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$.

Vậy D là một đỉnh của hình bình hành ABCD.

3. Bài tập tự luyện.

Bài 1. Cho tam giác ABC có M thỏa mãn điều kiện $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}$. Vị trí điểm M là:

A. M là điểm thứ tư của hình bình hành ACBM;

B. M là trung điểm của đoạn thẳng AB;

C. M trùng C;

D. M là trọng tâm tam giác ABC.

Bài 2. Cho tam giác ABC. Tập hợp các điểm M thỏa mãn $\left|\overrightarrow{MB}-\overrightarrow{MC}\right|=\left|\overrightarrow{BM}-\overrightarrow{BA}\right|$ là:

A. đường thẳng AB;               

B. trung trực đoạn  BC;

C. đường tròn tâm A bán kính BC;                 

D. đường thẳng qua A và song song với  BC.

Bài 3. Cho tam giác ABD. Xác định điểm C sao cho: $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$.

A. C là một đỉnh của hình bình hành ABCD;

B. C là trọng tâm tam giác ABD;

C. C là trung điểm AB;

D. C là trung điểm BD.

Bài 4. Cho 2 điểm A, B với A cố định. Xác định điểm B sao cho: $\left|\overrightarrow{AB}\right|=4$.

A. B là điểm thuộc đường tròn tâm A bán kính 2;

B. B là điểm thuộc đường tròn tâm A bán kính 4;

C. B là điểm thuộc đường tròn đi qua A bán kính 4;

D. B là điểm thuộc đường tròn đi qua A bán kính 2.

Bài 5. Cho 3 điểm A, B, M với B cố định. Xác định điểm A sao cho: $\left|MA-MB\right|=5$.

A. A là điểm thuộc đường tròn tâm M bán kính 5;

B. A là điểm thuộc đường tròn tâm B bán kính 5;

C. A là điểm thuộc đường tròn đi qua M bán kính 25;

D. A là điểm thuộc đường tròn đi qua B bán kính 25.

Bài 6. Cho đoạn thẳng AB, biết $\left|\overrightarrow{IA}\right|=\left|\overrightarrow{IB}\right|$. Xác định tập hợp điểm I.

A. Tập hợp điểm I là đường thẳng AB;

B. Tập hợp điểm I là đường tròn đường kính AB;

C. Tập hợp điểm I là đường trung trực của đoạn thẳng AB;

D. Tập hợp điểm I là đường tròn bán kính AB.

Bài 7. Cho hình bình hành ABCD và điểm M, biết $\left|\overrightarrow{BM}-\overrightarrow{BA}\right|=\left|\overrightarrow{AB}+\overrightarrow{AD}\right|$. Điểm M là:

A. Điểm thuộc đường tròn tâm A bán kính AC;

B. Điểm thuộc đường tròn tâm A bán kính BD;

C. Điểm thuộc đường tròn tâm B bán kính AC;

D. Điểm thuộc đường tròn tâm B bán kính BD.

Bài 8. Cho đoạn thẳng CD, biết $\left|\overrightarrow{MC}\right|=\left|\overrightarrow{DM}\right|$. Điểm M:

A. thuộc đường thẳng CD;

B. thuộc đường trung trực của đoạn thẳng CD;

C. thuộc đường tròn đường kính CD;

D. thuộc đường tròn bán kính CD.

Bài 9. Cho hình thoi ABCD tâm O và điểm I, biết $\left|\overrightarrow{BO}-\overrightarrow{MO}\right|=\left|\overrightarrow{OD}+\overrightarrow{OC}\right|$. Điểm I là:

A. Điểm thuộc đường tròn tâm O bán kính AC;

B. Điểm thuộc đường tròn tâm O bán kính BD;

C. Điểm thuộc đường tròn tâm B bán kính BC;

D. Điểm thuộc đường tròn tâm B bán kính AC.

Bài 10. Cho tam giác ABC và điểm K thỏa mãn $\overrightarrow{AK}+\overrightarrow{BK}+\overrightarrow{CK}=\overrightarrow{0}$. Xác định điểm K ?

A. K là điểm thứ tư của hình bình hành ACBK;

B. K là trung điểm của đoạn thẳng AB;

C. K trùng C;

D. K là trọng tâm tam giác ABC.