Phương pháp xác định vị trí tương đối giữa 2 đường thẳng hay, chi tiết - Toán lớp 10

---

Phương pháp xác định vị trí tương đối giữa 2 đường thẳng hay, chi tiết

Với Phương pháp xác định vị trí tương đối giữa 2 đường thẳng hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xác định vị trí tương đối giữa 2 đường thẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

Cho hai đường thẳng d₁ và d₂ và điểm A thuộc đường thẳng d₁:

+ Nếu hai đường thẳng này có cùng VTCP( hoặc VTPT) và điểm A không thuộc d₂ thì d₁// d₂

+ Nếu hai đường thẳng này có cùng VTCP( hoặc VTPT) và điểm A thuộc d₂ thì d₁≡ d₂

+ Nếu VTPT của đường thẳng này là VTCP của đường thẳng kia thì hai đường thẳng đó vuông góc với nhau.

+ Nếu hai VTCP ( hoặc VTPT) không cùng phương và có tích vô hướng khác 0 thì hai đường thẳng đó cắt nhau.

Chú ý: Cho hai vecto a→( x; y); b→( x'; y' ) thì tích vô hướng a→. b→ = xx’ + yy’.

Để hai vecto này vuông góc với nhau ⇔ xx’+ yy’ = 0

B. Ví dụ minh họa

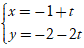
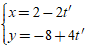
Ví dụ 1. Xét vị trí tương đối của hai đường thẳng d₁: và d₂:

A. Trùng nhau.

B. Song song.

C. Vuông góc với nhau.

D. Cắt nhau nhưng không vuông góc nhau.

Lời giải

+ Đường thẳng d₁ có VTCP u₁→( 1; -2).

+ Đường thẳng d₂ có VTCP u₂→( -2;4) và điểm B( 2; -8) thuộc đường thẳng này.

+ Thay tọa độ điểm B vào phương trình đường thẳng d₁ ta được :

⇔ t= 3

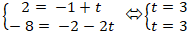
Suy ra điểm B thuộc đường thẳng d₁. (1)

+ Lại có u₂→ = -2u₁→ (2)

Từ (1) và ( 2) suy ra hai đường này trùng nhau.

Chọn A.

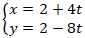
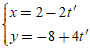
Ví dụ 2. Xét vị trí tương đối của hai đường thẳng d₁: và d₂: .

A. Trùng nhau.

B. Song song.

C. Vuông góc với nhau.

D. Cắt nhau nhưng không vuông góc nhau.

Lời giải

+ Đường thẳng d₁ có VTCP u₁→( 4; -8).

+ Đường thẳng d₂ có VTCP u₂→( -2;4) và điểm B( 2; -8) thuộc đường thẳng này.

+ Thay tọa độ điểm B vào phương trình đường thẳng d₁ ta được :

không có giá trị nào của t thỏa mãn.

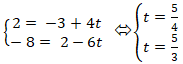
Suy ra điểm B không thuộc đường thẳng d₁. (1)

+ Lại có u₁→ = -2u₂→ (2)

Từ ( 1) và ( 2) suy ra: d₁// d₂

Chọn B.

Ví dụ 3. Xác định vị trí tương đối của hai đường thẳng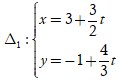
và .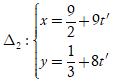

A. Trùng nhau.

B. Song song.

C. Vuông góc với nhau.

D. Cắt nhau nhưng không vuông góc nhau.

Lời giải

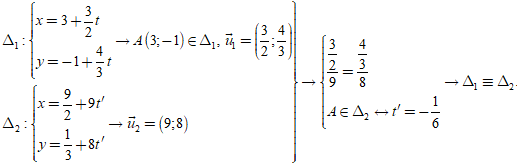
Chọn A

Ví dụ 4. Xác định vị trí tương đối của hai đường thẳng ∆₁: 7x + 2y - 1 = 0 và
∆₂: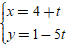

A. Trùng nhau.

B. Song song.

C. Vuông góc với nhau.

D. Cắt nhau nhưng không vuông góc nhau.

Lời giải

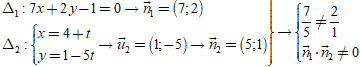
→ ∆₁, ∆₂ cắt nhau nhưng không vuông góc.

Chọn D.

Ví dụ 5. Xét vị trí tương đối của hai đường thẳng d₁: và d₂: 3x + 2y - 14 = 0.

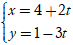
A. Trùng nhau.

B. Song song.

C. Vuông góc với nhau.

D. Cắt nhau nhưng không vuông góc nhau.

Lời giải

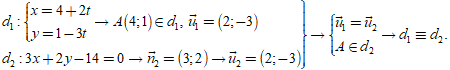
Chọn A

Ví dụ 6: Xét vị trí tương đối của hai đường thẳng d₁: và
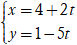
d₂: 5x + 2y - 14 = 0.

A. Trùng nhau.

B. Song song.

C. Vuông góc với nhau.

D. Cắt nhau nhưng không vuông góc nhau.

Lời giải

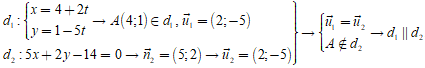
Chọn B.

Ví dụ 7. Đường thẳng nào sau đây có đúng một điểm chung với đường thẳng
d: ?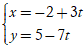

A. 7x + 3y - 1 = 0    B. 7x + 3y + 1 = 0

C. 3x - 7y + 2018 = 0    D. 7x + 3y + 10 = 0

Lời giải

Ta đưa đường thẳng d về dạng tổng quát:

Đường thẳng d: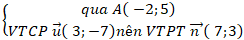

⇒ Phương trình tổng quát của d:

7( x + 2) + 3(y - 5) = 0 hay 7x + 3y - 1 = 0

+ Phương án A: Hai đường thẳng này trùng nhau.

+ đường thẳng d// d₂: 7x + 3y + 1 = 0 và d// d₃: 7x + 3y + 10 = 0

Chọn C.

Ví dụ 8. Tìm m để hai đường thẳng a: 2x - 3y + 4 = 0 và b: 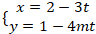cắt nhau.

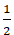
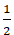
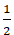
A. m ≠ -    B. m ≠ 2    C. m ≠    D. m =

Lời giải

Ta đưa phương trình đường thẳng b về dạng tổng quát:

Đường thẳng b: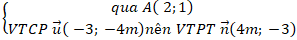

⇒ Phương trình đường thẳng b:

4m( x - 2) - 3( y - 1) = 0 hay 4m.x - 3y + 3 - 8m = 0

Để hai đường thẳng a và b cắt nhau khi và chỉ khi :

⇔ 2m ≠ 1 nên m ≠

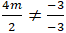
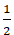
Chọn C.

Ví dụ 9 . Tìm tất cả các giá trị của m để hai đường thẳng d₁: và
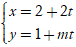
d₂: 4x - 3y + m = 0 trùng nhau.

A. m = -3    B. m = 1    C. m = 2    D. không có giá trị nào của m

Lời giải

+ Ta đưa đường thẳng d₁ về dạng tổng quát:

Đường thẳng d₁: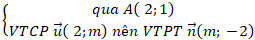

⇒ Phương trình tổng quát của đường thẳng d₁:

m( x - 2) - 2( y - 1) = 0 hay m.x - 2y + 2 - 2m = 0

+ Với m = 0 thì đường thẳng d₁ là : - 2y + 2 = 0 hay y - 1 = 0

⇒ hai đường thẳng d₁ và d₂ không trùng nhau nên m = 0 không thỏa mãn.

+ Xét m ≠ 0.

Để hai đường thẳng đã cho trùng nhau khi và chỉ khi :

vô lí vì

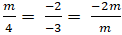
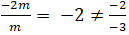
Vậy không có giá trị nào của m thỏa mãn.

Chọn D.

Ví dụ 10. Cho hai đường thẳng d₁ :2x+ 3y-19= 0 và d₂: 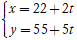. Tìm toạ độ giao điểm của hai đường thẳng đã cho.

A. ( 2; 5)    B. ( 4; -1)    C. ( -1 ; 6)    D. (4; 3)

Lời giải

Giao điểm của2 đường thẳng đã cho nếu có là nghiệm hệ phương trình:

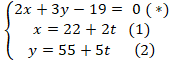
Thay (1) và (2) vào ( *) ta được :

2( 22 + 2t) + 3(55 + 5t) – 19 = 0

⇔ 44 + 4t + 165 + 15t - 19 = 0

⇔ 19t + 190 = 0 ⇔ t = -10

⇒ x = 2 và y = 5

Vậy giao điểm của hai đường thẳng đã cho là A( 2; 5)

Chọn A.

Ví dụ 11: Cho điểm A(0; -2) ; B( -1; 0); C(0; -4); D( -2; 0). Tìm tọa độ giao điểm của 2 đường thẳng AB và CD

A. (1; -2)    B. (0; 2)    C. Vô số    D. Không có giao điểm.

Lời giải

+ Đường thẳng AB đi qua A( 0; -2) có vectơ chỉ phương là AB→(-1;2) nên có VTPT (2; 1) .

⇒ Phương trình: AB: 2( x - 0) + 1( y + 2) = 0 hay 2x + y + 2 = 0

+ Đường thẳng CD có vectơ chỉ phương là CD→ = (-2; 4).

+ Ta có: AB→ = (-1; 2) và CD→ = (-2; 4) cùng phương và điểm C không thuộc AB nên và CD không có giao điểm.

Chọn D.

Ví dụ 12. Các cặp đường thẳng nào sau đây vuông góc với nhau?

A. d₁: 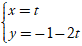và d₂: 2x + y - 1 = 0

B. d₁: x - 2 = 0 và d₂: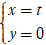

C. d₁: 2x - y + 3 = 0 và d₂: x - 2y + 1 = 0

D. d₁: 2x - y + 3 = 0 và d₂: 4x - 2y + 1 = 0

Lời giải

Hai đường thẳng vuông góc với nhau khi và chỉ khi :

+ Vecto pháp tuyến của đường thẳng này là vecto chỉ phương của đường thẳng kia.

+ Tích vô hướng của hai vecto chỉ phương của hai đường thẳng bằng 0.

+ Tích vô hướng của hai vecto pháp tuyến của 2 đường thẳng bằng 0.

Ta xét các phương án:

(i)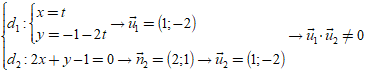 → loại A.

(ii) 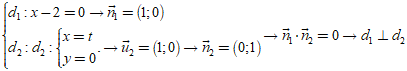Chọn B.

Tương tự, kiểm tra và loại các đáp án C, D.

Chọn B.

Ví dụ 13. Lập phương trình của đường thẳng ∆ đi qua giao điểm của hai đường thẳng (a):x + 3y - 1 = 0; (b):x - 3y - 5 = 0 và vuông góc với đường thẳng (c):2x - y + 7 = 0.

A. 3x + 6y - 5 = 0.    B. 6x + 12y - 5 = 0.

C. 6x + 12y + 7 = 0 .    D. x + 2y + 10 = 0.

Lời giải

Giao điểm của hai đường thẳng a và b nếu có là nghiệm hệ phương trình :

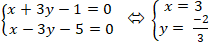
Vậy giao điểm của hai đường thẳng a và b là A(3; - )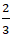

+ đường thẳng ∆: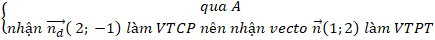

⇒Phương trình ∆: 1( x - 3) + 2( y + 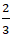) = 0

⇔ x + 2y - 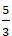= 0 ⇔ 3x + 6y – 5 = 0

Chọn A.

Ví dụ 14. Với giá trị nào của m thì hai đường thẳng d₁: 4x - 3y + 3m = 0 và
d₂: 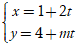vuông góc với nhau?

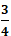
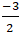
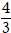
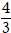
A. m =    B. m =    C. m = -    D. m =

Lời giải

+ đường thẳng d₁ có VTPT n→( 4; -3).

+ Đường thẳng d₂ đi qua M( 1; 4) và có VTCP u→( 2; m) nên nhận vecto n'→( m; -2) làm VTPT.

+ Để hai đường thẳng đã cho vuông góc với nhau khi và chỉ khi :

n→.n'→ = 0 ⇔ 4m - 3.(-2) = 0

⇔ 4m = - 6 ⇔ m =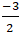

Chọn B.

Ví dụ 15. Tìm tọa độ giao điểm của đường thẳng d: 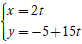và trục tung.

A. (1; 0)    B. (0; -5)    C. (5; 0)    D. (-2; 0)

Lời giải

Trục tung Oy có phương trình là x = 0

Giao điểm của đường thẳng d và trục tung nếu có lag nghiệm hệ phương trình:

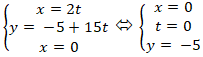
Vậy giao điểm của đường thẳng d và trục tung là điểm A( 0; -5)

Chọn B.

C. Bài tập vận dụng

Câu 1: Xét vị trí tương đối của hai đường thẳng d₁: và d₂:

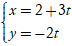
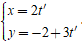
A. Trùng nhau.

B. Song song.

C. Vuông góc với nhau.

D. Cắt nhau nhưng không vuông góc nhau.

Lời giải:

Đáp án: C

Trả lời:

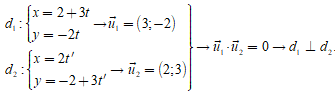
Câu 2: Cho hai đường thẳng d₁: và d₂:
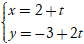
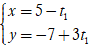
Khẳng định nào sau đây là đúng:

A. d₁ song song d₂.

B. d₁ và d₂ cắt nhau tại M( 1 ; -3) .

C. d₁ trùng với d₂

D. d₁ và d₂ cắt nhau tại M( 3 ; -1) .

Lời giải:

Đáp án: D

Trả lời:

Ta đưa phương trình hai đường thẳng về dạng tổng quát:

d₁: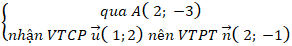

⇒Phương trình đường thẳng d₁:

2( x - 2) – 1( y + 3) = 0 hay 2x - y - 7 = 0

Đường thẳng d₂: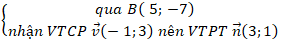

⇒ Phương trình đường thẳng d₂:

3( x - 5) + 1( y + 7) = 0 hay 3x + y - 8 = 0

+ Giao điểm của d₁ và d₂ là nghiệm hệ phương trình :

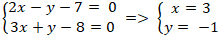
Vậy giao điểm của hai đường thẳng đã cho là M(3; -1) .

Câu 3: Cho hai đường thẳng d₁: 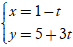và d₂: x - 2y + 1 = 0.
Khẳng định nào sau đây là đúng:

A. d₁ song song d₂.

B. d₂ song song với trục Ox.

C. d₂ cắt trục Oy tại M(0; ) .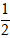

D. d₁ và d₂ cắt nhau tại M( ; ) .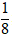

Lời giải:

Đáp án: C

Trả lời:

Ta đưa đường thẳng d₁ về dạng tổng quát :

Đường thẳng d₁: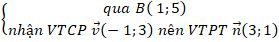

⇒ Phương trình đường thẳng d₁:

3( x - 1) + 1( y - 5) = 0 hay 3x + y – 8 = 0

+ Giao điểm của hai đường thẳng đã cho là nghiệm hệ phương trình :

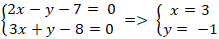
Vậy giao điểm của hai đường thẳng đã cho là M( ; ) .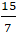

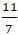
⇒ A, B, D sai.

+ Giao điểm của d₂ và trục Oy là nghiệm hệ :

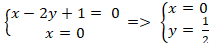
Câu 4: Cho bốn điểm A(4; -3) ; B( 5; 1) ; C( 2; 3)và D( -2; 2) . Xác định vị trí tương đối của hai đường thẳng AB và CD.

A. Trùng nhau.

B. Song song.

C. Vuông góc với nhau.

D. Cắt nhau nhưng không vuông góc nhau.

Lời giải:

Đáp án: D

Trả lời:

Đường thẳng AB nhận vecto AB→ = ( 1; 4) làm VTCP.

Đường thẳng CD nhận vecto CD→ = ( - 4; -1) làm VTCP.

Ta thấy: 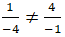và AB→.CD→ ≠ 0

⇒ AB và CD cắt nhau nhưng không vuông góc.

Câu 5: Cho bốn điểm A(1; 2) ; B( 4; 0); C( 1; -3) và D(7; -7). Xác định vị trí tương đối của hai đường thẳng AB và CD.

A. Trùng nhau.

B. Song song.

C. Vuông góc với nhau.

D. Cắt nhau nhưng không vuông góc nhau.

Lời giải:

Đáp án: B

Trả lời:

Ta viết phương trình đường thẳng AB:

AB: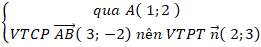

⇒ Phương trình đường thẳng AB: 2( x - 1) + 3( y - 2) = 0

Hay ( AB): 2x + 3y – 8 = 0

+ đường thẳng CD nhận VTCP CD→( 6; -4) cùng phương với AB→.

Lại có; điểm C không thuộc đường thẳng AB.

⇒ Hai đường thẳng AB và CD song song với nhau.

Câu 6: Đường thẳng nào sau đây không có điểm chung với đường thẳng
d: x - 3y + 4 = 0?

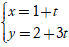
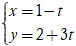
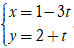
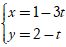
A.    B.    C.    D.

Lời giải:

Đáp án: D

Trả lời:

Nhận xét:

+ Hai đường thẳng có hai VTPT cùng phương thì hai đường thẳng đó song song hoặc trùng với nhau.

+ Hai đường thẳng có hai VTPT không cùng phương thì hai đường thẳng đó cắt nhau.

Đường thẳng d có VTPT n→( 1; -3)

(i) Xét đáp án A:

d₁: 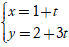→ n₁→ = (1; 3) → n₁→, n→ không cùng phương nên loại A.

(ii) Xét đáp án B:

d₂: 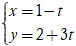→ n₂→ = (3; 1) → n₂→, n→ không cùng phương nên loại B.

(iii) Xét đáp án C:

d₃: 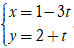→ n₃→ = (1; 3) → n₃→, n→ không cùng phương nên loại C.

(iv) Xét đáp án D:

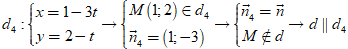
Câu 7: Đường thẳng nào sau đây có vô số điểm chung với đường thẳng d: ?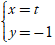

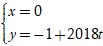
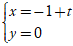
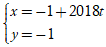
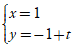
A.    B.    C.    D.

Lời giải:

Đáp án: C

Trả lời:

Hai đường thẳng có hai điểm chung thì chúng trùng nhau. Như vậy bài toán trở thành tìm đường thẳng trùng với đường thẳng đã cho lúc đầu.

Ta đưa các đường thẳng về dạng tổng quát:

+ đường thẳng d: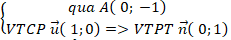

⇒ Phương trình đường thẳng d: 0( x - 0) + 1( y + 1) = 0 hay y + 1 = 0

+ Xét phương án A:

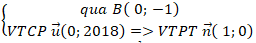
Đường thẳng này có VTPT khác với đường thẳng d nên hai đường thẳng này không thể trùng nhau .

+ Xét phương án B: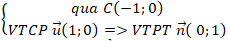

⇒ Đường thẳng này và đường thẳng d có cùng VTPT và điểm C không thuộc đường thẳng d nên hai đường thẳng này song song với nhau.

+ Xét phương án C: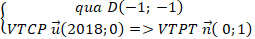

⇒ Phương trình tổng quát của đường thẳng:

0( x + 1) + 1( y + 1) = 0 hay y + 1 = 0

⇒ đường thẳng này trùng với đường thẳng d.

Câu 8: Với giá trị nào của m thì hai đường thẳng
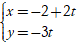
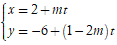
d₁: và d₂: trùng nhau?

A. m = 1/2.    B. m = -2    C. m = 2    D. m = 1

Lời giải:

Đáp án: C

Trả lời:

Để hai đường thẳng trùng nhau khi và chỉ khi hai đường thẳng đó có cùng VTCP và có một điểm chung .

Đường thẳng d₁ có VTCP là: u→( 2; -3) .

Đường thẳng d₂ có VTCP là v→( m; 1- 2m) và đi qua điểm A( 2; -6) .

Để hai đường thẳng này trùng nhau khi và chỉ khi

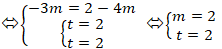
Vậy với m= 2 thì hai đường thẳng đã cho trùng nhau.

Câu 9: Với giá trị nào của m thì hai đường thẳng
d₁: 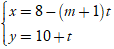và d₂: mx + 2y - 14 = 0 song song?

A. m = 1 hoặc m = -2.    B. m = 1    C. m =-2    D. không có giá trị nào của m .

Lời giải:

Đáp án: A

Trả lời:

+ Đường thẳng d₁: qua M( 8;10) và nhận VTCP u→( -m - 1; 1) nên nhận vecto
n→( 1; m + 1) làm VTPT.

+ đường thẳng d₂ nhận vecto n'→( m;2) làm VTPT.

+ Nếu m= 0 thì đường thẳng d₁ có VTPT là n→( 1; 1) và đường thẳng d₂ có VTPT là
n'→( 0; 2)

⇒ Hai vecto này không cùng phương nên hai đường thẳng đã cho không song song .

⇒ m = 0 không thỏa mãn.

+ Nếu m ≠ 0. Để hai đường thẳng đã cho song song với nhau khi và chỉ khi điểm M không thuộc d₂ và hai VTPT cùng phương

⇔ m = 1 hoặc m = -2

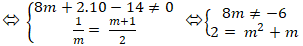
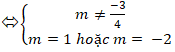
Câu 10: Tìm toạ độ giao điểm của hai đường thẳng
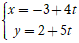
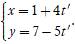
d₁: và d₂:

A. (1;7)    B. (2; 4)    C. (3; -1)    D. (4; -1)

Lời giải:

Đáp án: A

Trả lời:

Giao điểm của hai đường thẳng đã cho nếu có là nghiệm hệ phương trình:

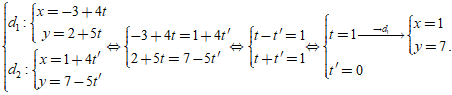
Câu 11: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(-2;0) ; B(1;4) và đường thẳng d: . Tìm tọa độ giao điểm của đường thẳng AB và d.

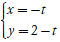
A. (2; 0)    B. (-2; 0)    C. (0; 2)    D. (0; -2)

Lời giải:

Đáp án: B

Trả lời:

+ Viết phương trình đường thẳng AB:

( AB) :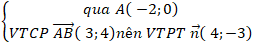

⇒ Phương trình AB: 4(x + 2) – 3( y - 0) = 0

Hay: 4x - 3y + 8 = 0.

+ Giao điểm của đường thẳng d và AB nếu có là nghiệm hệ phương trình

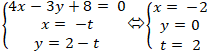
Vậy giao điểm của d và AB là M( -2; 0).

Câu 12: Xác định a để hai đường thẳng d₁: ax + 3y - 4 = 0 và d₂: cắt nhau tại một điểm nằm trên trục hoành.

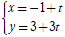
A. a = 1    B. a = -1    C. a = 2    D. a = -2

Lời giải:

Đáp án: D

Trả lời:

Gọi giao điểm của d₁ và d₂ thỏa mãn đề bài là A(x; 0) .

⇒ điểm A thuộc đường thẳng d₂ nên hệ phương trình sau có nghiệm :

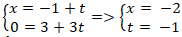
Vậy giao điểm của hai đường thẳng d₁ và d₂ là A(-2; 0) .

Do điểm A thuộc d₁ nên ta có: -2.a + 3.0 - 4 = 0 ⇔ a = -2

Câu 13: Tìm tất cả các giá trị của tham số m để hai đường thẳng d₁: 4x + 3my - m² = 0 và d₂: cắt nhau tại một điểm thuộc trục tung.

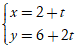
A. m = 0 hoặc m = -6.    B. m = 0 hoặc m = 2.

C. m = 0 hoặc m = -2.    D. m = 0 hoặc m = 6

Lời giải:

Đáp án: D

Trả lời:

Gỉa sử hai đường thẳng d₁ và d₂ cắt nhau tại điểm A(0; y) thuộc trục tung.

Do điểm A thuộc đường thẳng d₂ nên ta thay tọa độ của điểmA vào phương trình đường thẳng d₂ ta được:

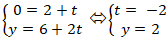
⇒ Tọa độ điểm A( 0; 2) .

+ Mà điểm A thuộc đường thẳng d₁ nên ta có:

4.0 + 3m.2 - m² = 0 ⇔ -m² + 6m = 0 ⇔ m = 0 hoặc m = 6

Câu 14: Đường thẳng nào sau đây vuông góc với đường thẳng d: 4x - 3y + 1 = 0?

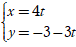
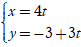
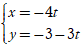
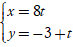
A.    B.    C.    D.

Lời giải:

Đáp án: A

Trả lời:

Nhận xét: Hai đường thẳng vuông góc với nhau khi và chỉ khi:

+ Tích vô hướng của hai VTCP( hoặc VTPT) của hai đường thẳng bằng 0.

+ VTCP của đường thẳng này là VTPT của đường thẳng kia.

Đường thẳng d nhận VTPT là : n→( 4; -3)

(i) Xét đáp án A: có VTCP u→( 4; -3)

⇒ VTCP của đườngthẳng này là VTPT của đường thẳng d nên hai đường thẳng này vuông góc với nhau.

Câu 15: Với giá trị nào của m thì hai đường thẳng (a): 2x - 3y - 10 = 0 và
(b): 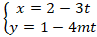vuông góc?

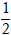
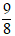
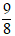
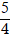
A. m =    B. m =    C. m =    D. m = -

Lời giải:

Đáp án: C

Trả lời:

Đường thẳng (a) nhận vecto n→( 2; -3) làm VTPT

Đường thẳng (b) nhận vecto u→( -3; -4m)làm VTCP nên nhận n'→( 4m; -3) làm VTPT.

Hai đường thẳng vuông góc với nhau khi và chỉ khi tích vô hướng của hai VTPT của hai đường thẳng đó bằng 0:

⇔ n→.n'→ = 0 ⇔ 2.4m – 3.(-3) = 0 ⇔ 8m = 9 ⇔ m=