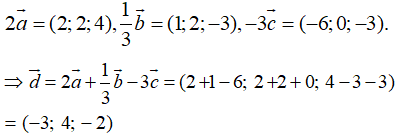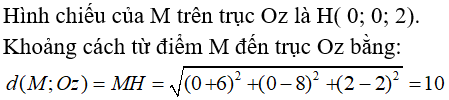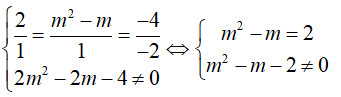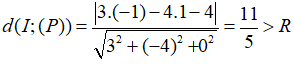Trắc nghiệm Đề kiểm tra Chương 3 Hình học 12 có đáp án năm 2023
Trắc nghiệm Đề kiểm tra Chương 3 Hình học 12 có đáp án năm 2023
Với bộ Trắc nghiệm Đề kiểm tra Chương 3 Hình học 12 có đáp án năm 2023 sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Hình học lớp 12.
Câu 1: Trong không gian Oxyz, cho hai vectơ u→ = (x; y; z), u'→ = (x'; y'; z') . Trong các khẳng định sau đây, khẳng định nào sai?
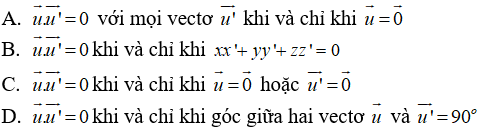
Câu 2: Trong không gian Oxyz, cho ba vectơ
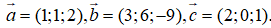
Tọa độ của vectơ:
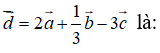
A. (-3;4;4) B. (-3;4;-2) C. (9;4;4) D. Đáp án khác
Câu 3: Trong không gian Oxyz, cho điểm M(x0; y0; z0) với x0, y0, z0 ≠ 0. Gọi M1, M2, M3 lần lượt là hình chiếu vuông góc của điểm M trên các trục Ox, Oy, Oz. Trong các khẳng định sau, khẳng định nào sai?
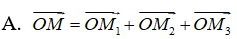
B. M1(x0; 0; 0), M2(0; y0; 0), M3(0; 0; z0)
C. OM ≤ OM1 + OM2 + OM3
D. Mặt phẳng (M1M2M3) đi qua điểm M
Câu 4: Trong không gian Oxyz, cho hai điểm A(1; 3; 1), B(0; 1; 2). Với những giá trị nòa của m thì điểm C(0;0;m) nằm trên đường thẳng AB
A. m = 1 B. m = 2 C. m = 0 D. Không tồn tại m
Câu 5: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D' có A(1; 0; 0), B(2; 0; 0), D(1; 2; 0), A'(1; 0; 2). Gọi I là tâm của hình hộp. Trong các khẳng định sau đây, khẳng định nào sai?
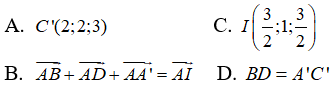
Câu 6: Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(-4;0;0), B(0;2;0), C(0;0;-4). Phương trình của mặt cầu (S) là:
A. x2 + y2 + z2 + 2x - y + 2z = 0 C. x2 + y2 + z2 - 4x + 2y - 4z = 0
B. x2 + y2 + z2 + 4x + 2y + 4z = 0 D. x2 + y2 + z2 + 4x - 2y + 4z = 0
Câu 7: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và chứa trục Ox. Phương trình của mặt phẳng (P) là:
A. x + 2y + 3z - 14 = 0 C. 2x - y = 0
B. 3y - 2z = 0 D. 3x - z = 0
Câu 8: Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua ba điểm A(1;2;3), B(2;0;1), C(-1;1;-2) là:
A. 8x + 9y - 5z - 11 = 0 C. 9x + 7y - 4z - 14 = 0
B. 4x - 9y - 7z + 1 = 0 D. 7x - 4y + 9z - 23 = 0
Câu 9: Trong không gian Oxyz, cho hai điểm A(3;1;-1), B(2;-1;4) và mặt phẳng (Q) có phương trình là: 2x - y + 3z - 1 = 0 . Cho (P) là mặt phẳng đi qua A, B và vuông góc với (Q). Trong các khẳng định sau, khẳng định nào sai?
A. nQ→ vuông góc với vectơ pháp tuyến của mặt phẳng (P)
B. Một vectơ pháp tuyến của mặt phẳng (P) là:
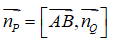
C. Phương trình tổng quát của mặt phẳng (P) là: x + 2y - 5z - 10 = 0
D. Cả hai khẳng định A và B đều đúng
Câu 10: Trong gian Oxyz, cho ba mặt phẳng : (P): x - y + 2z + 1 = 0 , (Q): x + 3my - z = 0 , (R): ms - y + z = 0 . Tìm m để giao tuyến của hai mặt phẳng (Q) và (R) vuông góc với mặt phẳng (P).
A. m=1 B. m C. m=-1 D. Không tồn tại m
Câu 11: Trong không gian Oxyz, cho ba điểm A(6; 0; 0), B(0; 6; 0), C(0; 0; 6). Gọi G là trọng tâm của tam giác ABC. Trong những khẳng định dưới đây, khẳng định nào sai?
A. Tọa độ của điểm G(2;2;2)
B. OG ⊥ (ABC)
C. Phương trình đường cao hạ từ đỉnh O của tứ diện OABC là: x = t, y = t, z = t
D. Tứ diện OABC là tứ diện đều
Câu 12: Trong không gian Oxyz, cho đường thẳng d đi qua điểm M(1;3;4) và song song với đường thẳng Δ: x = 1 + 2t, y = 1 - 3t, z = 3 + 2t . Phương trình chính tắc của đường thẳng d là:
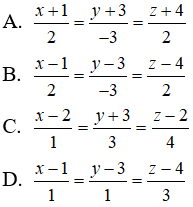
Câu 13: Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm M(2;1;-3) và song song với hai mặt phẳng: (P): 3x + y - 2z = 0, (Q): y - 3z = 0 .
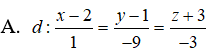
B. d: x = 2 + t, y = 1 - 9t, z = -3 - 3t
C. d: x = -2 + t, y = -1 - 9t, z = 3 - 3t
D. d: x = 2 + t, y = 1 + 9t, z = -3 - 3t
Câu 14: Trong không gian Oxyz, khoảng cách từ M(-6;8;2) đến trục Oz bằng:
A. 10 B. 2 C. √104 D. √28
Câu 15: Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x + y - 2z = 0; 2x + (m2 - m)y - 4z + 2m2 - 2m - 4 = 0, trong đó m là tham số. Tìm m để hai mặt phẳng (P) và (Q) song song
A. m=1 hoặc m=-2 C. m=-2
B. m=1 D. Không có m thỏa mãn bài toán
Câu 16: Trong không gian Oxyz, tính khoảng cách giữa hai đường thẳng:
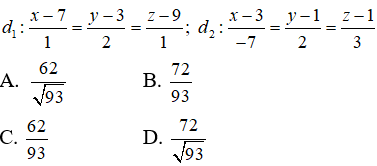
Câu 17: Tìm tất cả các giá trị của a để hai đường thẳng sau cắt nhau: d1: x = 1 + at, y = t, z = -1 + 2t, d2: x = 1 + t', y = 2 - 2t', z = 3 + t'
A. a > 0 B. a ≠ 4/3 C. a = 0 D. a ≠ 0
Câu 18: Trong không gian Oxyz, cho mặt cầu (S): (x + 1)2 + (y - 1)2 + (z - 1)2 = 4 và mặt phẳng (P): 3x - 4y - 4 = 0 . Có bao nhiêu đường thẳng d nằm trong mặt phẳng (P), đi qua điểm M(0;-1;2) và tiếp xúc với mặt cầu (S)
A. 0 B. 1 C. 2 D. Vô số
Câu 19: Trong không gian Oxyz, cho bốn điểm A(3;1;-1), B(1;1;1), C(2;1;0), D(-3;5;1). Có bao nhiêu mặt phẳng đồng thời cách đều cả bốn điểm A, B, C, D?
A. 0 B. 4 C. 7 D. Vô số
Câu 20: Cho các số a, b, c, m, n, p thay đổi nhưng luôn thỏa mãn các điều kiện: a2 + b2 + c2 + 4a - 2b - 4c ≤ 0 và 2m + 2n - p - 11 = 0. Tìm giá trị nhỏ nhất của biểu thức: P = (a - m)2 + (b - n)2 + (c - p)2
A. 0 B. 4 C. 2 D. 9
Hướng dẫn giải và Đáp án
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Đáp án | C | B | D | D | B | D | B | A | C | A |
| Câu | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Đáp án | D | B | B | A | D | A | C | A | D | B |
Câu 1:
Nếu u→.u'→ = 0 thì chưa thể kết luận u→ = 0→ hoặc u'→ = 0→
Câu 2:
Ta có:
Câu 3:
Gọi M1, M2, M3 lần lượt là hình chiếu vuông góc của điểm M trên các trục Ox, Oy, Oz.
Tọa độ các điểm M1; M2 và M3 lần lượt là:
M1(x0; 0; 0), M2(0; y0; 0), m3(0; 0; z0)
Phương trình mặt phẳng (M1M2M3) là:
Câu 4:
Câu 5:
Áp dụng quy tắc hình hộp ta có:
AB→ + AD→ + AA'→ = AC'→ = 2AI→
Do đó, khẳng định B là sai
Câu 6:
Câu 7:
Ta có: OM→(1; 2; 3)
Vì mặt phẳng (P) đi qua điểm M(1;2;3)
Và chứa trục Ox nên mặt phẳng (P) nhận vecto [OM→;j→] làm vecto pháp tuyến.
Phương trình của mặt phẳng (P) là:
0(x - 1) + 3(y - 2) - 2(z - 3) = 0 hay 3y – 2z = 0
Câu 8:
Ta có: AB→(1; -2; -2); AC→(-2; -1; -5)
Vì mặt phẳng (P) đi qua ba điểm A ; B; C nên mặt phẳng này nhận vecto [AB→;AC→] = (8; 9; -5) làm vecto pháp tuyến .
Phương trình mặt phẳng (P):
8(x - 1) + 9(y - 2) – 5 (z – 3) = 0 hay 8x + 9y – 5z -11= 0
Câu 9:
Trong không gian Oxyz, cho hai điểm A(3;1;-1), B(2;-1;4) và mặt phẳng (Q) có phương trình là: 2x - y + 3z = 0 . Cho (P) là mặt phẳng đi qua A, B và vuông góc với (Q). Trong các khẳng định sau, khẳng định nào sai?
+ Mặt phẳng (Q) có VTPT là nQ→(2; -1; 3)
+ vì mặt phẳng (P) vuông góc với mặt phẳng ( Q) nên nQ→(2; -1; 3) vuông góc với vectơ pháp tuyến của mặt phẳng (P)
+ Một vectơ pháp tuyến của mặt phẳng (P) là: np→ = [AB→,nQ→]
+ Ta có: AB→(-1; -2; 5); [AB→;nQ→] = (-1; 13; 5)
Phương trình tổng quát của mặt phẳng (P) là:
-1(x - 3) + 13(y - 1) + 5(z + 1) = 0
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 14:
Câu 15:
Mặt phẳng (P) đi qua điểm O(0;0;0) .
Để hai mặt phẳng (P) và (Q) song song thì hai vecto pháp tuyến cùng phương và điểm O không thuộc mặt phẳng (Q).
Suy ra, không có m thỏa mãn bài toán
Câu 16:
Câu 17:
Câu 18:
Mặt cầu (S) có tâm I(-1; 1; 1 ), bán kính R = 2.
Khoảng cách từ tâm I đến mp(P) là:
Suy ra, mặt phẳng (P) không cắt mặt cầu nên không có đường thẳng d nào trong mặt phẳng (P) thỏa mãn đầu bài.
Câu 19:
Câu 20:
Chọn đáp án B
