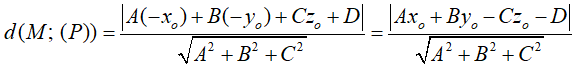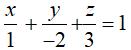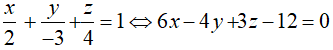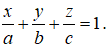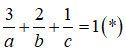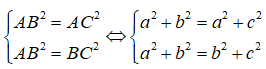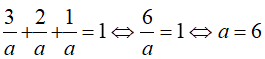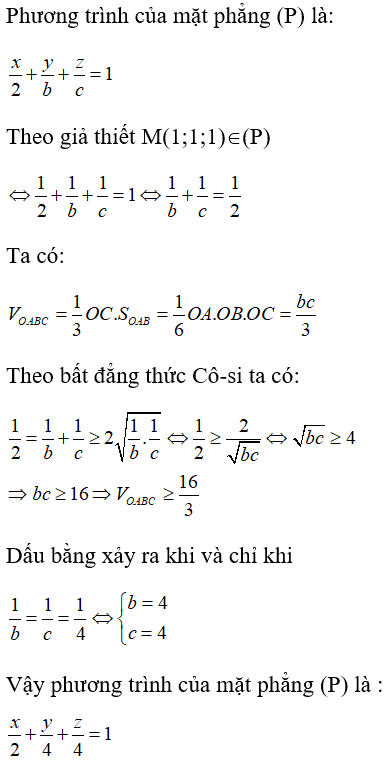Trắc nghiệm Phương trình mặt phẳng có đáp án năm 2023
Trắc nghiệm Phương trình mặt phẳng có đáp án năm 2023
Với bộ Trắc nghiệm Phương trình mặt phẳng có đáp án năm 2023 sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Hình học lớp 12.
Câu 1: Trong không gian Oxyz, cho hai điểm A(1;0;-2), B(-1;1;1). Phương trình mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là:
A. 2x - y - 3z - 8 = 0 C. x - 2z - 8 = 0
B. x - 2z - 8 = 0 D. 2x - y - 3z + 6 = 0
Do (P) ⊥ AB nên mp(P) có một vectơ pháp tuyến là nP→ = AB→ = (-2; 1; 3) . Mặt khác (P) đi qua điểm A nên phương trình của mặt phẳng (P) là:
-2(x - 1) + (y - 0) + 3(z + 2) = 0 ⇔ -2x + y + 3z + 8 = 0 ⇔ 2x - y - 3z - 8 = 0.
Vậy đáp án đúng là A.
Lưu ý. Khi ta viết phương trình mặt phẳng (P) bị nhầm ở cột z:
-2(x - 1) + (y - 0) + 3(z + 2) = 0 <> 2x - y - 3z - 4 = 0
thì ta được đáp án B.
Khi ta viết phương trình mặt phẳng bị nhầm giữa tọa độ của điểm A với tọa độ của vectơ pháp tuyến 1(x - (-2)) + 0(y - 1) -2(z - 3) = 0 <=> x - 2x + 8 = 0 thì ta được đáp án C.
Khi ta viết phương trình mặt phẳng đi qua B thì ta thu được đáp án D.
Câu 2: Trong không gian Oxyz, cho hai điểm A(1;3;5), B(-1;5;3). Lập phương trình mặt phẳng trung trực (P) của đoạn thẳng AB
A. x + y + z = 0 B. x + y - z = 0 C. x - y + z = 0 D. -x + y + z = 0
Mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB. Ta có
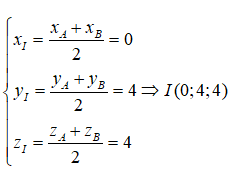
Ta chọn :
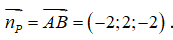
Vậy phương trình của mặt phẳng (P) là:
-2(x - 0) + 2(y - 4) - 2(z - 4) = 0 ⇔ -2x + 2y - 2z = 0 ⇔ x - y + z = 0
Vậy đáp án đúng là C.
Câu 3: Trong không gian Oxyz, gọi A1, A2, A3 lần lượt là hình chiếu vuông góc của điểm A(4;3;2) trên các trục Ox, Oy, Oz. Trong các khẳng định sau, khẳng định nào sai?
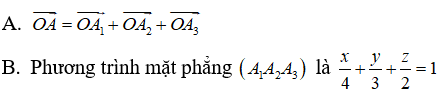
C. Thể tích của tứ diện OA1A2A3 bằng 4
D. Mặt phẳng (A1A2A3) đi qua điểm A.
Vì A1, A2, A3 lần lượt là hình chiếu vuông góc của điểm A(4;3;2) lên các trục Ox, Oy, Oz nên ta có A1(4; 0; 0), A2(0; 3; 0), A3(0; 0; 2) .
Từ đó suy ra các khẳng định A và B là đúng.
Thể tích của khối tứ diện
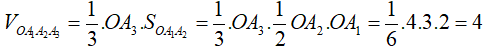
Vậy khẳng định C là đúng.
Khẳng định D là sai do
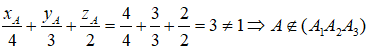
Vậy đáp án cần tìm là đáp án D.
Câu 4: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;1 ;-3), vuông góc với mặt phẳng (Q) : x + y - 3z = 0 đồng thời (P) song song với trục Oz.
A. x + y - 3 = 0 B. x - y - 1 = 0 C. 2x + y - 3z - 1 = 0 D. x - y + 1 = 0
Từ giả thiết ta suy ra
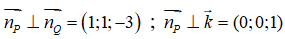
Ta chọn
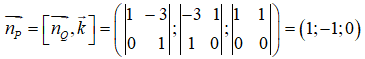
Mặt khác (P) đi qua điểm A(2 ;1 ;-3) nên ta có phương trình của mặt phẳng (P) là : 1(x - 2) - 1(y - 1) = 0 <=> x - y - 1 = 0 .
Vậy đáp án đúng là B
Lưu ý. Đáp án A xuất phát từ việc tính sai thành phần thứ hai của vectơ pháp tuyến
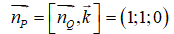
Đáp án C xuất phát từ sai lầm trong công thức viết phương trình mặt phẳng, nhầm giữa tọa độ của điểm và tọa độ của vectơ pháp tuyến
Đáp án D xuất phát từ việc nhầm hệ số tự do khi viết phương trình mặt phẳng (P).
Câu 5: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1 ;0 ;1), B(0 ;-1 ;-3), C(3 ;2 ;5).
A. x - y - 1 = 0 B. x - y + 1 = 0 C. x + z - 2 = 0 D. x + y - 1 = 0
Từ giả thiết ta suy ra
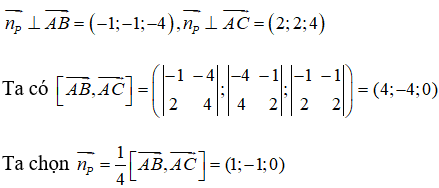
Mặt khác (P) đi qua điểm A(1 ;0 ;1) nên ta có phương trình của mặt phẳng (P) là : 1(x - 1) - 1(y - 0) = 0 <=> x - y - 1 = 0.
Vậy đáp án đúng là A.
Câu 6: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1 ;2 ;2) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 2x + 2y + z - 8 = 0
B. 2x + 2y + z + 8 = 0
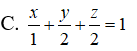
D. x + 2y + 2z - 9 = 0
Ta có OA ⊥ OB, OC => OA ⊥ (OBC) => OA ⊥ BC .
Mặt khác ta có AM ⊥ BC nên ta suy ra BC ⊥ (OAM) => BC ⊥ OM
Chứng minh tương tự ta được AC ⊥ OM . Do đó OM ⊥ (ABC).
Ta chọn nP→ = OM→ = (1; 2; 2). Từ đó suy ra phương trình của mặt phẳng (P) là :
1(x - 1) + 2(y - 2) + 2(z - 2) = 0 <=> x + 2y + 2z - 9 = 0
Chọn D
Lưu ý. Bài toán này có thể giải bằng cách tìm tọa độ của các điểm A, B, C dựa vào các điều kiện
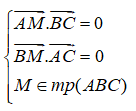
Câu 7: Trong không gian Oxyz, cho mặt phẳng (P) có phương trình (m2 - 2m)x + y + (m - 1)z + m2 + m = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) song song với trục Ox ?
A. m=0 B. m=2 C. m=0 hoặc m=2 D. m=1
Ta có nP→ = (m2 - 2m; 1; m - 1). Mặt phẳng (P) song song với trục Ox khi và chỉ khi
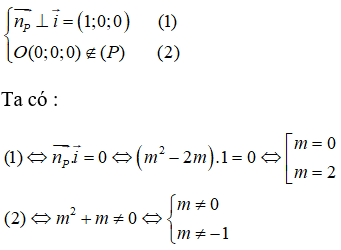
Từ đó ta được m=2.
Vậy đáp án B là đáp án đúng.
Lưu ý. Học sinh thường chỉ để ý đến điều kiện (1) và quên mất điều kiện (2), từ đó sẽ chọn đáp án (C)
Câu 8: Trong không gian Oxyz, cho hai mặt phẳng (P) : x + 2y - 2z + 1 = 0, (Q): 2x + 4y + az + b = 0. Tìm a và b sao cho khoảng cách giữa hai mặt phẳng đó bằng 1.
A. a=-4 và b=8 C. a=-2 và b=38 hoặc b=-34
B. a=-4 và b=8 hoặc b=-4 D. a=-4 và b=38 hoặc b=-34
Muốn khoảng cách giữa hai mặt phẳng (P) và (Q) lớn hơn 0 thì trước hết hai mặt phẳng đó phải song song (nếu hai mặt phẳng đó trùng nhau hoặc cắt nhau thì khoảng cách giữa chúng sẽ bằng 0). Do đó ta có:
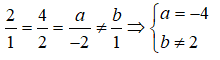
Lấy điểm A(-1;0;0) ∈ (P). Khi đó ta có:
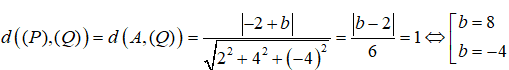
Vậy đáp an đúng là B.
Lưu ý. Đáp án A sai là do khi tính khoảng cách quên không lấy giá trị tuyệt đối
Đáp án D sai, xuất phát từ sai lầm khi tính khoảng cách bị sai do thiếu căn thức ở mẫu số.
Đáp án C sai, do trong trường hợp đó hai mặt phẳng cắt nhau, khoảng cách giữa hai mặt phẳng này sẽ bằng 0.
Câu 9: Trong không gian Oxyz, cho mặt cầu (S) có phương trình là x2 + y2 + z2 - 2x - 4y + 6z + 5 = 0 và cho mặt phẳng (P) : x - 2y + 3z + 3 = 0. Khẳng định nào dưới đây là đúng ?
A. (P) giao (S) theo một đường tròn
B. (P) tiếp xúc với (S)
C. (P) không cắt (S)
D. Mặt phẳng (P) đi qua tâm của mặt cầu (S)
Mặt cầu (S) có tâm I(1;2;-3) và có bán kính
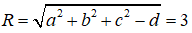
Khoảng cách từ tâm I đến mặt phẳng (P) là:
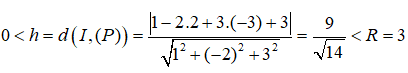
Do đó mặt phẳng (P) giao với mặt cầu (S) theo một đường tròn và (P) không đi qua tâm I của (S).
Vậy đáp án đúng là A.
Câu 10: Trong không gian Oxyz, cho ba điểm thay đổi A(a; 0; 0), B(0; b; 0), C(0; 0; c) trong đó a, b, c khác 0 và thỏa mãn điều kiện 3ab + bc - 2ac = abc . Khoảng cách lớn nhất từ O đến mặt phẳng (ABC) là:
A. 14 B. √14 C. 1/√14 D. Không tồn tại
Phương trình của mặt phẳng (ABC) là:
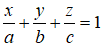
Theo giả thiết ta có:
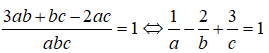
Từ đó suy ra M(1; -2; 3) ∈ mp(ABC) .
Gọi H là hình chiếu vuông góc của O trên mp(ABC). Ta có:
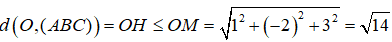
Dấu bằng xảy ra khi và chỉ khi H trùng M.
Vậy đáp án đúng là B
Câu 11: Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(x0, y0, z0) và có một vectơ pháp tuyến nP→ = (A; B; C) là:
A. Ax0 + By0 + Cz0 = 0
B. A(x + x0) + B(y + y0) + C(z + z0) = 0
C. A(x - x0) + B(y - y0) + C(z - z0) = 0
D. x0(x - A) + y0(y - B) + z0(z - C) = 0
Phương trình của mặt phẳng (P) đi qua điểm M(x0; y0; z0) và có một vectơ pháp tuyến np→ = (A; B; C) là:
A(x - x0) + B(y - y0) + C(z - z0) = 0
Câu 12: Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(-x0, y0, -z0) và có một vectơ pháp tuyến nP→ = (-A; B; -C) là:
A. A(x - x0) - B(y - y0) + C(z - z0) = 0
B. A(x + x0) - B(y - y0) + C(z + z0) = 0
C. A(x - x0) - B(y + y0) + C(z - z0) = 0
D. A(x + x0) - B(y + y0) + C(z + z0) = 0
Phương trình của mặt phẳng (P) đi qua điểm M(-x0; y0; -z0) và có một vectơ pháp tuyến np→ = (-A; B; -C) là:
-A(x + x0) + B(y - y0) - C(z + z0) = 0
⇔ A(x + x0) - B(y - y0) + C(z + z0) = 0
Câu 13: Trong không gian Oxyz, cho điểm M(-x0; -y0; z0) và phương trình của mặt phẳng (P): Ax + By + Cz = D = 0 . Khoảng cách từ điểm M đến mặt phẳng (P) là:
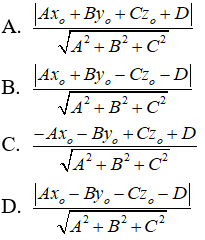
Khoảng cách từ điểm M đến mặt phẳng (P) là:
Câu 14: Trong không gian Oxyz, cho hai mặt phẳn song song (P): Ax + By + Cz + D = 0 và (Q): Ax + By + Cz + D' = 0. M là một điểm di động trên mặt phẳng (P). Khẳng định nào dưới đây có thể sai?
A. Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
B. Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
C. Khoảng cách giữa hai mặt phẳng (P) và (Q) là
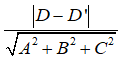
D. Khoảng cách giữa hai mặt phẳng (P) và (Q) là |D' - D|
Nếu hai mặt phẳng (P) và (Q) song song với nhau và M thuộc mặt phẳng (P) thì:
+ Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) là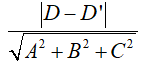 
+ Đặc biệt, khoảng cách giữa hai mặt phẳng (P) và (Q) là |D - D'| khi và chỉ khi :
A2 + B2 + C2 =1
Do đó, mệnh đề D có thể sai.
Câu 15: Trong các khẳng định dưới đây, khẳng định nào đúng?
A. Mỗi mặt phẳng chỉ có duy nhất một vectơ pháp tuyến
B. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và biết một vectơ pháp tuyến của mặt phẳng (P)
C. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và (P) vuông góc với một mặt phẳng (Q) cho trước
D. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và (P) song song với một đường thẳng d cho trước
Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A(x0; y0; z0) thuộc (P) và biết một vectơ pháp tuyến n→(A; B; C) của mặt phẳng (P).
Phương trình mặt phẳng (P) khi đó: A(x - x0) + B(y - y0) + C(z - z0)= 0
Câu 16: Trong các khẳng định dưới đây, khẳng định nào sai?
A. Phương trình của mặt phẳng (P) đi qua điểm M(x0; y0; z0) và có một vectơ pháp tuyến nP→ = (A; B; C) là: A(x - x0) + B(y - y0) + C(z - z0) = 0
B. Nếu hai mặt phẳng vuông góc với nhau thì hai vectơ pháp tuyến của chúng cũng vuông góc
C. Nếu hai mặt phẳng cắt nhau thì hai vectơ pháp tuyến của chúng không cùng phương
D. Nếu hai mặt phẳng (P) và (Q) có hai vectơ pháp tuyến cùng phương thì chúng song song
Khẳng định: Nếu hai mặt phẳng (P) và (Q) có hai vectơ pháp tuyến cùng phương thì chúng song song là sai vì khi đó hai mặt phẳng (P) và (Q) có thể trùng nhau.
Câu 17: Trong không gian Oxyz, cho mặt phẳng (P) có phương trình là x - 2y + 2 = 0 . Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P):
Mặt phẳng (P) có phương trình là x - 2y + 2 = 0 . Một vectơ pháp tuyến của mặt phẳng (P): n3→ = (1; -2; 0)
Câu 18: Trong không gian Oxyz, cho mặt phẳng (P) có phương trình là
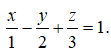
Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P):
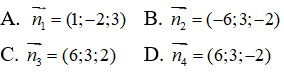
Câu 19: Trong không gian Oxyz, phương trình tổng quát của mặt phẳng (Oxy) là:
A. x=0 B. y=0 C. z=0 D. x+y=0
Phương trình mặt phẳng (Oxy) là z = 0.
Câu 20: Trong không gian Oxyz, phương trình tổng quát của mặt phẳng (P) đi qua điểm M(1;-2;3) và song song với mặt phẳng (Oxy) là:
A. x – 1 = 0 B. y + 2 = 0 C. z – 3 = 0 D. Đáp án khác
Mặt phẳng (Oxy) có phương trình là: z = 0.
Mặt phẳng này có vecto pháp tuyến là: k→ = (0; 0; 1)
Vì mặt phẳng (P) song song với mặt phẳng (Oxy)
nên mặt phẳng này nhận vecto np→ = k→ = (0; 0; 1) làm vecto pháp tuyến.
Mặt khác (P) đi qua điểm M(1;-2;3) nên (P) có phương trình là:
1.(z - 3) = 0 ⇔ z - 3 = 0
Câu 21: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;-1 ;3) và song song với mặt phẳng (Q) :
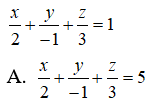
B. x - 2y + 3z - 15 = 0
C. 3x - 6y + 2z - 18 = 0
D. 3x - 6y + 2z + 18 = 0
Phương trình mặt phẳng (Q) viết lại dưới dạng: 3x - 6y + 2z - 6 = 0
Do đó ta có thể chọn
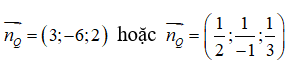
Vì mp (P) // mp(Q) nên mp(P) có VTPT là
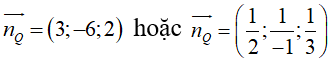
Suy ra đáp án B sai. Trong ba đáp án còn lại chỉ có mặt phẳng ở đáp án C đi qua điểm A.
Câu 22: Trong không gian Oxyz, lập phương trình mặt phẳng (P) đi qua điểm A(2 ;-1 ;-2) và song song với mặt phẳng (Q) : 2x - y + 2z = 0
A. 2x - y + 2z - 1 = 0 C. 2x - y - 2z + 1 = 0
B. 2x - y + 2z + 9 = 0 D. 2x - y + 2z + 1 = 0
Vì mặt phẳng (P) song song với mặt phẳng (Q) : 2x – y + 2z = 0 nên mặt phẳng (P) có dạng : 2x – y + 2z + d = 0
Mà mặt phẳng (P) đi qua điểm A(2; -1; -2) nên:
2.2 –(-1) + 2.(-2) + d = 0 nên d = -1
Vậy phương trình mặt phẳng (P) là: 2x – y + 2z – 1= 0
Câu 23: Trong không gian Oxyz, lập phương trình mặt phẳng (P) đi qua điểm A(-2 ;1 ;-2) và vuông góc với trục Oz.
A. x + y + 1 = 0 B. -2x + y - z + 1 = 0
C. z - 1 = 0 D. z + 2 = 0
Do mặt phẳng (P ) vuông góc trục Oz nên mặt phẳng này nhận vecto k→ = (0; 0; 1) làm vecto pháp tuyến.
Lại có:
Điểm A(-2 ; 1 ; -2) thuộc mặt phẳng (P) nên phương trình (P): 0(x + 2) + 0( y - 1) + 1(z + 2)= 0 hay z + 2= 0
Câu 24: Trong không gian Oxyz, cho hai điểm A(1 ;0 ;-2), B(-1 ;1 ;2). Phương trình của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là:
A. 2x - y - 4z - 10 = 0 C. x - y - 2z - 5 = 0
B. 2x - y - 4z + 10 = 0 D. 2x - y - 3z + 8 = 0
Do (P) → AB nên mp(P) có một vectơ pháp tuyến là
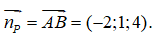
Mặt khác (P) đi qua điểm A nên phương trình của mặt phẳng (P) là
-2(x - 1) + (y - 0) + 4(z + 2) = 0 ⇔ 2x - y - 4z - 10 = 0
Câu 25: Trong không gian Oxyz, cho hai điểm A(1;3;-2), B(1;1;2). Gọi (P) là mặt phẳng trung trực của đoạn thẳng AB. Phương trình của mặt phẳng (P) là:
A. y - 2z - 2 = 0 B. y - 2z - 7 = 0 C. y - 2z + 3 = 0 D. 2y + z - 4 = 0
Mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB.
Ta có:
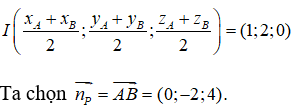
Vậy phương trình của mặt phẳng (P) là:
0(x - 1) - 2(y - 2) + 4(z - 0) = 0
⇔ -2y + 4z + 4 = 0 ⇔ y - 2z - 2 = 0
Câu 26: Trong không gian Oxyz, cho điểm M(1;-2;3). Gọi M1, M2, M3 lần lượt là hình chiếu vuông góc của điểm M trên các trục Ox, Oy, Oz. Trong các khẳng định dưới đây, khẳng định nào sai?
A. M1(1; 0; 0)
B. M2(0; 2; 0)
C. M3(0; 0; 3)
D.Phương trình của mặt phẳng (M1M2M3) là:
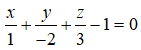
Với điểm M(1;-2;3). Gọi M1, M2, M3 lần lượt là hình chiếu vuông góc của điểm M trên các trục Ox, Oy, Oz thì tọa độ M1(1; 0; 0); M2 (0 ;-2; 0) và M3( 0; 0; 3).
Phương trình mặt phẳng M1M2M3 là:
Câu 27: Trong không gian Oxyz, cho điểm A(2;-3;4). Lập phương trình mặt phẳng (P) đi qua các hình chiếu vuông góc của điểm A trên các trục tọa độ:
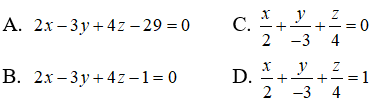
Với điểm A(2;-3;4). Hình chiếu của A trên 3 trục tọa độ lần lượt là:
B(2; 0; 0); C( 0; -3; 0) và D( 0; 0; 4).
Phương trình mặt phẳng (BCD)là:
Câu 28: Trong không gian Oxyz, cho điểm M(1;2;3). Lập phương trình mặt phẳng đi qua M sao cho (P) cắt các trục Ox, Oy, Oz lần lượt tại A, B, C và M là trọng tâm của tam giác ABC
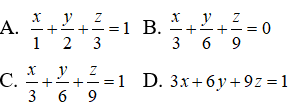
Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c). Vì M(1;2;3) là trọng tâm của tam giác ABC nên ta có:
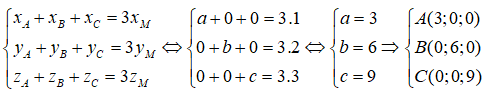
Vậy phương trình của mặt phẳng (P) là:
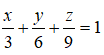
Câu 29: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;-2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC
A. 6x - 3y -2z - 6 = 0
B. x - 2y + 3z + 14 = 0
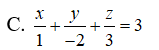
D. x - 2y + 3z - 14 = 0
Ta có: OA → OB, OC => OA → (OBC) => OA → BC
Mặt khác vì AM → BC (M là trực tâm tam giác ABC) nên ta suy ra BC → (OAM) => BC → OM
Chứng minh tương tự ta được AC → OM. Do đó OM → (ABC). Ta chọn: np→ = OM→ = (1; -2; 3)
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) - 2(y + 2) + 3(z - 3) = 0 ⇔ x - 2y + 3z - 14 = 0
Câu 30: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(3;2;1) và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O) sao cho tam giác ABC đều. Số mặt phẳng (P) thỏa mãn bài toán là:
A. 1 B. 2 C. 3 D. 4
Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c > 0 . Phương trình của mặt phẳng (P) là:
Vì M(3 ;2 ;1) thuộc (P) nên ta có :
Vì tam giác ABC đều nên ta có :
⇔ a2 = b2 = c2 ⇔ a = b= c (do a, b, c > 0)
Thay a = b = c vào phương trình (*) ta được
Suy ra: a = b = c = 6. Vậy có một mặt phẳng (P) thỏa mãn bài toán.
Câu 31: Trong không gian Oxyz, cho mặt phẳng (P) thay đổi nhưng luôn đi qua hai điểm là A(2;0;0), M(1;1;1). Cho (P) cắt các tia Oy, Oz lần lượt tại các điểm B, C (khác O). Viết phương trình mặt phẳng (P) sao cho thể tích của từ diện OABC nhỏ nhất.
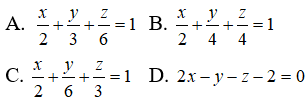
Gọi B(0; b; 0), C(0; 0; c), trong đó b, c > 0.
Ta có: OA = 2; OB = b; OC = c
Câu 32: Trong không gian Oxyz, cho hai vectơ u→ = (-1; 3; 4), v→ = (2; -1; 5). Tích có hướng của hai vectơ u→ và v→ là:
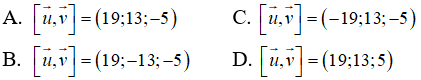
Hai vectơ u→ = (-1; 3; 4), v→ = (2; -1; 5)
Thì tích có hướng của hai vectơ u→ và v→ là:
[u→,v→] = (19; 13; -5)
Câu 33: Trong không gian Oxyz, cho mặt phẳng (P) đi qua ba điểm A(1;1;1), B(2;3;-1), C(0;3;-2). Một vectơ pháp tuyến của mặt phẳng (P) là:
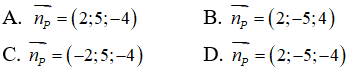
Từ giả thiết ta suy ra
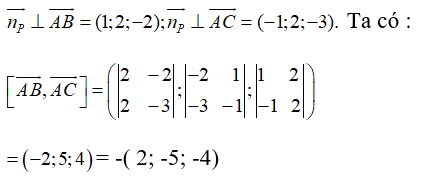
Từ đó suy ra np = (2; -5; -4)→ là một vectơ pháp tuyến của (P)
