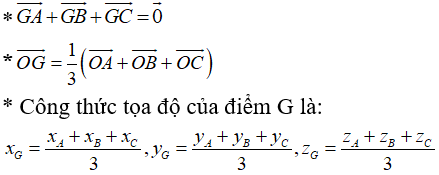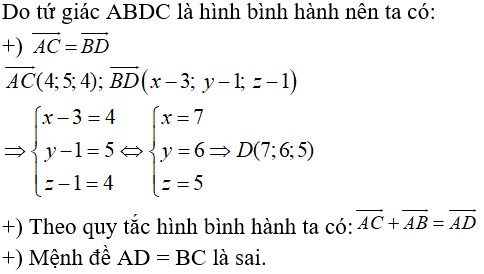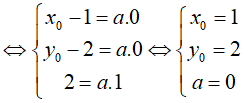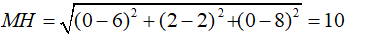Trắc nghiệm Ôn tập Chương 3 Hình học 12 có đáp án có đáp án năm 2023
Trắc nghiệm Ôn tập Chương 3 Hình học 12 có đáp án có đáp án năm 2023
Với bộ Trắc nghiệm Ôn tập Chương 3 Hình học 12 có đáp án có đáp án năm 2023 sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Hình học lớp 12.
Câu 1: Trong không gian Oxyz, cho vectơ
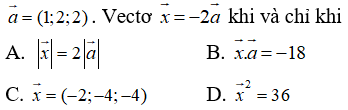
Câu 2: Trong không gian Oxyz, cho tam giác ABC. Điều kiện nào dưới đây không tương đương với điều kiện G là trọng tâm của tam giác ABC.
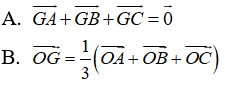
C. Công thức tọa độ của điểm G là:
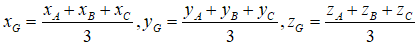
D. OA + OB + OC ≥ 3OG
G là trọng tâm của tam giác ABC khi và chỉ khi một trong các điều kiện xảy ra:
Câu 3: Trong không gian Oxyz, cho ba điểm A(3; 0; 0), B(0; 3; 0), C(0; 0; 3). Gọi G là trọng tâm tam giác ABC. Trong các khẳng định sau, khẳng định nào sai?
A. OA = OB = OC B. GA = GB = GC C. OG ⊥ (ABC) D. OG = 3
Câu 4: Trong không gian Oxyz, cho hình bình hành ABDC. Biết rằng A(1;3;5), B(3;1;1), C(5;8;9). Trong các khẳng định sau, khẳng định nào sai?
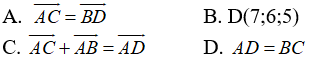
Câu 5: Trong không gian Oxyz, cho hai điểm A(1; 2; 3), B(x0, y0, 5) . Đường thẳng AB song song với trục Oz khi và chỉ khi:
A. x0 = 1 C. x0 = 1 và y0 = 2
B. x0 = y0 = 0 D. x0 = 1 hoặc y0 = 2
Trục Oz có vecto chỉ phương là k→(0; 0; 1)
Lại có: AB→(X0 - 1; y0 - 2; 2)
Để đường thẳng AB song song với trục Oz khi và chỉ khi hai vecto AB→; k→ cùng phương
Tồn tại số a khác 0 sao cho: AB→ = a.k→
Câu 6: Trong không gian Oxyz,lập phương trình mặt phẳng (P) đi qua điểm A(2;1;-3) và vuông góc với trục Oy
A. x + z + 1 = 0 B. y - 1 = 0 C. y + 1 = 0 D. 2x + y - 3z - 1 = 0
Vì mặt phẳng (P) vuông góc với trục Oy nên nhận vecto j→(0; 1; 0) làm vecto pháp tuyến.
Phương trình mặt phẳng(P) là:
0(x - 2) + 1(y - 1) + 0(z + 3) = 0 hay y – 1 = 0
Câu 7: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua hai điểm A(1;0;1), B(2;1;3) và song song với trục Oz
A. x - y + 1 = 0 B. x + y - 1 = 0 C. x - y - 1 = 0 D. x + z - 1 = 0
Ta có: AB→(1; 1; 2)
Trục Oz có vecto chỉ phương k→(0; 0; 1).
Vì mặt phẳng (P) đi qua hai điểm A , B và song song trục Oz nên mặt phẳng này vecto
[AB→; k→] = (1; -1; 0) làm vecto pháp tuyến.
Phương trình mặt phẳng (P):
1(x - 1) -1(y - 0)+ 0( z - 1) = 0 hay x – y - 1= 0
Câu 8: Trong không gian Oxyz, cho mặt phẳng (P) có phương trình (m2 + m)x + y + (m - 2)z + m2 - m = 0 , trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) song song với trục Ox?
A. m = -1 B. m = 0 hoặc m = -1 C. m = 0 D. m = 2
Mặt phẳng (P) song song với trục Ox khi và chỉ khi
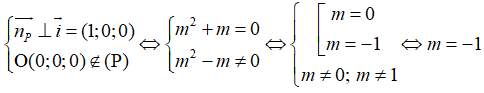
Câu 9: Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x + y - 2z = 0; 2x + (m2 + m)y - 4z + 2m2 + 2m - 4 = 0 , trong đó m là tham số. Với những giá trị nào của m thì hai mặt phẳng (P) và (Q) song song.
A. m = 1 hoặc m = -2 C. m = -2
B. m = 1 D. Không có m thỏa mãn
Hai mặt phẳng (P) và (Q) có vecto pháp tuyến là np→(1; 1 ; -2); nQ→ = (2; m2 + m; -4)
Hai mặt phẳng (P) và (Q) song song khi và chỉ khi tồn tại một số thực k sao cho
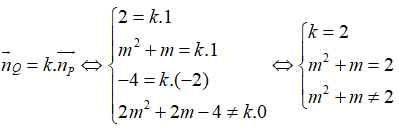
Hệ trên vô nghiệm. Vậy không tồn tại m thỏa mãn bài toán.
Câu 10: Trong không gian Oxyz, cho mặt cầu (S): (x + 1)2 + (y + 2)2 + (z - 3)2 = 1. Lập phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S) tại điểm A(-1;-2;4)
A. z - 2 = 0 hoặc z + 2 = 0 C. z - 2 = 0 hoặc z - 4 = 0
B. z - 4 = 0 D. z + 2 = 0
Mặt cầu (S) có tâm I(-1; -2; 3)
Vì mặt phẳng (P) tiếp xúc với mặt cầu (S) tại điểm A nên mặt phẳng (P) nhận vectơ nP→ = IA→ = (0; 0; 1) là vectơ pháp tuyến.
Vậy phương trình của mặt phẳng (P) là: 0(x + 1) + 0(y + 2) + 1(z - 4) = 0 ⇔ z - 4 = 0
Câu 11: Trong không gian Oxyz, cho hai mặt phẳng (P): x + 2y + z + 1 = 0 và (Q): 2x + 4y + az + b = 0 . Tìm a và b sao cho khoảng cách giữa hai mặt phẳng đó bằng 1.
A. a = 4 và b = 8 C. a = -2 và b = 38 hoặc b = -34
B. a = 4 và b = 8 hoặc b = -4 D. a = 4 và b = 38 hoặc b = -34
Để khoảng cách giưa hai mặt phẳng (P) và (Q) lớn hơn 0 thì trước hết hai mặt phẳng đó phải song song (nếu hai mặt phẳng đó trùng nhau hoặc cắt nhau thì khoảng cách giữa chúng sẽ bằng 0). Do đó ta có:
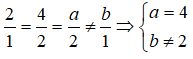
Lấy điểm A(-1;0;0) ∈ (P). Khi đó ta có:
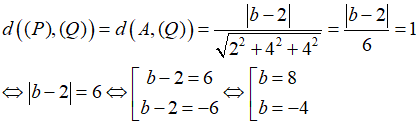
Câu 12: Trong không gian Oxyz, cho M là một điểm thay đổi trên mặt cầu (S) có tâm I(2;2;2), bán kính R=1. Tập hợp những điểm M’ đối xứng với điểm M qua gốc tọa độ là mặt cầu (S’) có phương trình là:
A. (x - 2)2 + (y - 2)2 + (z - 2)2 = 1 C. (x + 2)2 + (y - 2)2 + (z - 2)2 = 1
B. (x - 2)2 + (y + 2)2 + (z - 2)2 = 1 D. (x + 2)2 + (y + 2)2 + (z + 2)2 = 1
Tập hợp những điểm M’ đối xứng với điểm M qua gốc tọa độ là mặt cầu (S’) có tâm I’( -2; -2; -2) – là điểm đối xứng với tâm I qua gốc tọa độ O và bán kính R’ = R = 1.
Phương trình mặt cầu (S’) là: (x + 2)2 + (y + 2)2 + (z + 2)2 = 1
Câu 13: Cho mặt cầu (S) có phương trình: x2 + y2 + z2 - 2x + 4y - 6z - 2 = 0. Điểm M(m; -2; 3) nằm ngoài mặt cầu khi và chỉ khi:
A. m < -3 hoặc m > 5 B. m < -3 C. -3 ≤ m ≤ 5 D. m > 5
Mặt cầu (S) có tâm
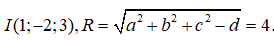
M nằm ngoài mặt cầu (S) khi và chỉ khi:
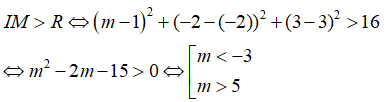
Câu 14: Trong không gian Oxyz, cho đường thẳng d đi qua điểm M(1;-2;-6) và vuông góc với mặt phẳng (P): x + 2y + 6z - 3 = 0. Trong những khẳng định dưới đây, khẳng định nào đúng?
A. Vectơ (1;2;6) vuông góc với vectơ chỉ phương của đường thẳng d
B. Phương trình của đường thẳng d là: 1(x - 1) + 2(y + 2) + 6(z + 6) = 0
C. Phương trình chính tắc của đường thẳng d là:
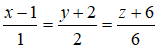
D. Cả ba khẳng định trên đều sai
Vì đường thẳng d vuông góc với mặt phẳng (P) nên d có vectơ chỉ phương là ud→ = uP→ = (1; 2; 6) .
Phương trình chính tắc của đường thẳng d là:
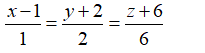
Từ đó suy ra C là khẳng định đúng.
Câu 15: Trong không gian Oxyz, lập phương trình chính tắc của đường thẳng d đi qua điểm M(0;1;-1), nằm trong mặt phẳng (P): x + 2y + z - 1 = 0 và vuông góc với đương thẳng
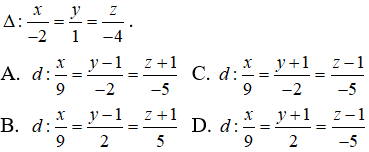
Ta có : np→(1; 2; 1); uΔ→ = (-2; 1; -4)
Vì đường thẳng d nằm trong mặt phẳng (P) và vuông góc với đường thẳng ∆ nên một vecto chỉ phương của đường thẳng d là ud→ = [uΔ→; np→] = (9; -2; -5)
Phương trình chính tắc của đường thẳng d :
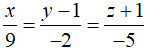
Câu 16: Trong không gian Oxyz, cho đường thẳng d là giao tuyến của hai mặt phẳng (P): 2x + y + z + 5 = 0, (Q): 2x - z + 3 = 0 . Phương trình tham số đường thẳng d là:
A. x = 1 + t, y = 8 + 4t, z = 3 + 2t C. x = 2t, y = 8 + 4t, z = 3 + 4t
B. x = t, y = -8 + 4t, z = 3 + 2t D. x = t, y = -8 - 4t, z = 3 + 2t
Tọa độ các điểm thuộc d là nghiệm của hệ phương trình :
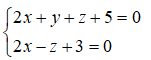
Đặt x = t, thay vào hệ trên ta được
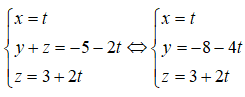
Câu 17: Trong không gian Oxyz, khoảng cách từ M(6;2;8) đến trục Oy bằng:
A. 10 B. 2 C. √104 D. √28
Hình chiếu vuông góc của điểm M trên trục Oy là điểm H(0 ;2 ;0). Vậy khoảng cách từ điểm M đến đường thẳng Oy bằng:
Câu 18: Trong không gian Oxyz, cho mặt phẳng (P): 3x - 4y + 18 = 0 và mặt cầu (S): (x - 1)2 + (y - 2)2 + (z + 3)2 = 4. Khẳng định nào dưới đây là đúng?
A. (P) và (S) có vô số điểm chung C. (P) tiếp xúc với (S)
B. (P) không cắt (S) D. Cả ba khẳng định trên đều sai
Mặt cầu (S) có tâm I(1 ;2 ;-3) và có bán kính R=2. Khoảng cách từ I đến mặt phẳng (P) là
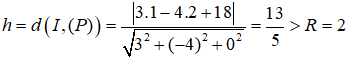
Câu 19: Cho đường thẳng d có phương trình: x = 2t, y = 1 - t, z = 3 + t và mặt phẳng (P) có phương trình: x + y + z - 10 = 0 . Trong những khẳng định dưới đây, khẳng định nào đúng?
A. d nằm trong mặt phẳng (P) C. d vuông góc với mặt phẳng (P)
B. d song song với mặt phẳng (P) D. d cắt mặt phẳng (P) tại điểm H(6;-2;6)
Do vectơ chỉ phương của đường thẳng d không vuông góc, cũng không cùng phương với vectơ pháp tuyến của mặt phẳng (P) nên ta suy ra các đáp án A, B, C là sai. Vậy D là đáp án đúng
Câu 20: Trong không gian Oxyz, tìm những điểm M trên tia Oz sao cho khoảng cách từ M đến mặt phẳng (P): 4y + 3z + 1 = 0 bằng 2
Gọi M(0 ;0 ;m) với m 0. Ta có :
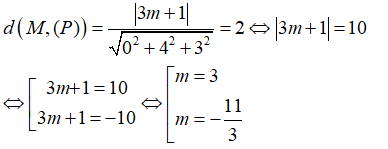
Kết hợp với điều kiện m ≥ 0 ta được m=3. Vậy M(0 ;0 ;3)
Câu 21: Trong không gian Oxyz, cho điểm A di động trên trục Ox, điểm B di động trên mặt phẳng (P): 2y - z - 2 = 0 . Khoảng cách giữa hai điểm A và B nhỏ nhất là:
Ta có Ox song song với mặt phẳng (P). Khoảng cách nhỏ nhất giữa hai điểm A và B chính là khoảng cách giữa trục Ox và mặt phẳng (P), dấu bằng xảy ra khi và chỉ khi AB vuông góc với (P). Mặt khác vì O thuộc Ox nên ta có :
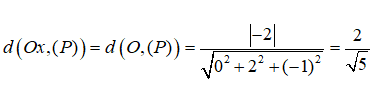
Vậy khoảng cách giữa hai điểm A và B nhỏ nhất là : 2/√5
Câu 22: Tính khoảng cách giữa hai đường thẳng chéo nhau sau đây:
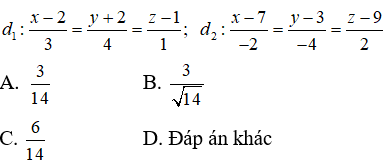
Đường thẳng d1 đi qua điểm M(2; -2; 1), VTCP u1→ = (3; 4; 1)
Đường thẳng d2 đi qua điểm N( 7; 3; 9), VTCP u2→ = (-2; -4; 2)
Ta có: MN→(5; 5; 8); [u1→;u2→] = (12; -8; -4)
Khoảng cách giữa hai đường thẳng đã cho là:
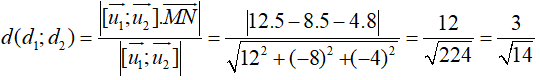
Câu 23: Trong không gian Oxyz, cho ba điểm A(0; -2; -4), B(-4; -4; 2), C(2; -3; 3). Tìm tọa độ của điểm M trên mặt phẳng (Oxz) sao cho biểu thức MA2 + MB2 + 2MC2 đạt giá trị nhỏ nhất
A. M1(0; 0; -1) B. M2(0; 0; 1) C. M3(0; -3; 0) D. M4(1; 0; -1)
Chọn đáp án B
Câu 24: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;-3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O) sao cho tam giác ABC đều. Số mặt phẳng (P) thỏa mãn bài toán là:
A. 1 B. 2 C. 3 D. 4
Gọi tọa độ A(a; 0; 0); B(0; b; 0) và C(0; 0; c)
Riêng trường hợp a = b = c là không thỏa mãn phương trình (1).
Các trường hợp còn lại đều có các giá trị của a, b , c thỏa mãn phương trình
Do đó, có 3 mặt phẳng (P) thỏa mãn phương trình .
Câu 25: Trong không gian Oxyz, cho điểm A di động trên mặt cầu (S): (x - 1)2 + (y + 1)2 + (z - 2)2 = 4 và mặt phẳng (P): 2x + 2y - z + 29 = 0 . Khoảng cách từ điểm A đến mặt phẳng (P) nhỏ nhất là:
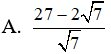
B. 1 C. 7 D. 11
Mặt cầu (S) có tâm I(1 ;-1 ;2) và có bán kính R=2. Khoảng cách từ điểm I đến mặt phẳng (P) là:
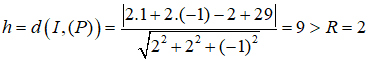
Do đó mặt phẳng (P) không cắt mặt cầu (S)
Gọi K và H lần lượt là hình chiếu vuông góc cúa A và I trên mặt phẳng (P). Ta có: d(A, (P)) = AK ≥ IK - IA ≥ IH - R = h - R = 9 - 2 = 7
Dấu bằng xảy ra khi và chỉ khi A là giao điểm của tia IH với mặt cầu (S). Vậy đáp án đúng là A.
