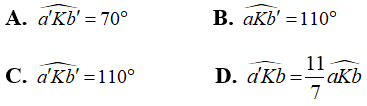200 Bài tập trắc nghiệm Toán lớp 7 Chương 1 Hình học có đáp án
200 Bài tập trắc nghiệm Toán lớp 7 Chương 1 Hình học có đáp án
Với bộ 200 Bài tập trắc nghiệm Toán lớp 7 Chương 1 Hình học có đáp án, chọn lọc sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 7.
- Bài tập Hai góc đối đỉnh
- Bài tập Hai đường thẳng vuông góc
- Bài tập Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài tập Hai đường thẳng song song
- Bài tập Tiên đề Ơ-clit về đường thẳng song song
- Bài tập Từ vuông góc đến song song
- Bài tập Định lí
- Tổng hợp Trắc nghiệm Chương 1 Hình Học 7
Bài tập Hai góc đối đỉnh có lời giải
Bài 1: Hai đường thẳng zz' và tt' cắt nhau tại A. Góc đối đỉnh với ∠zAt là:
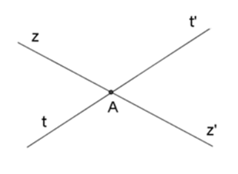
Vì hai đường thẳng zz' và tt' cắt nhau tại A nên Az' là tia đối của tia Az, At' là tia đối của tia At. Vậy góc đối đỉnh với ∠zAt' là ∠z'At.
Chọn đáp án B.
Bài 2: Cho góc xBy đối đỉnh với góc x'By' và ∠xBy = 60°. Tính số đo góc x'By'
A. 30° B. 120° C. 90° D. 60°
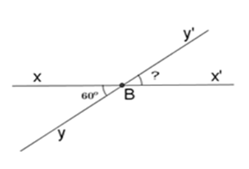
Vì ∠xBy là góc đối đỉnh với ∠x'By'. Khi đó: ∠xBy = ∠x'By' = 60° (tính chất hai góc đối đỉnh)
Chọn đáp án D.
Bài 3: Cho hai đường thẳng xx' và yy' giao nhau tại O sao cho ∠xOy = 45°. Chọn câu sai:
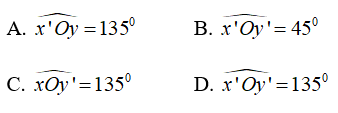
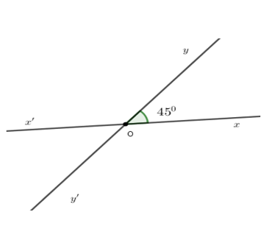
Vì hai đường thẳng xx' và yy' cắt nhau tại O nên Ox' là tia đối của tia Ox, Oy' là tia đối của tia Oy.
⇒ ∠xOy và ∠ x'Oy' ; ∠x'Oy và ∠xOy' là hai cặp góc đối đỉnh
Do đó ∠xOy = ∠x'Oy' = 45° và ∠x'Oy = ∠xOy'
Lại có ∠xOy và ∠x'Oy là hai góc ở vị trí kề bù nên ∠xOy + ∠x'Oy = 180°
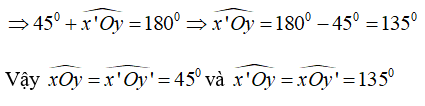
Suy ra A, B, C đúng, D sai.
Chọn đáp án D.
Bài 4: Cho cặp góc đối đỉnh ∠tOz và ∠t'Oz' (Oz và Oz' là hai tia đối nhau). Biết ∠tOz' = 4∠tOz. Tính các góc ∠tOz và ∠t'Oz'
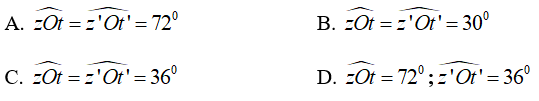
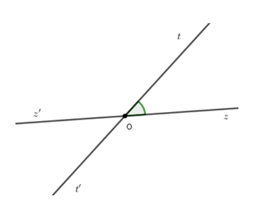
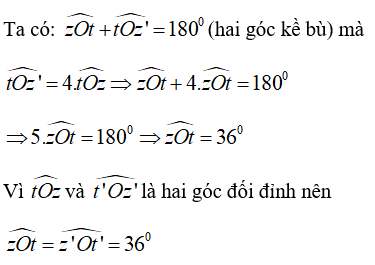
Chọn đáp án C.
Bài 5: Vẽ ∠ABC = 56°. Vẽ ∠ABC' kề bù với ∠ABC. Sau đó vẽ tiếp ∠C'BA' kề bù với ∠ABC'. Tính số đo ∠C'BA'
A. 124° B. 142° C. 65° D. 56°
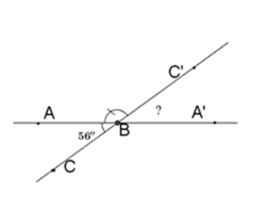
Vì ∠ABC' kề bù với ∠ABC nên BC' là tia đối của tia BC.
Vì ∠C'BA' kề bù với ∠ABC' nên BA' là tia đối của tia BA .
Do đó, ∠C'BA' và ∠ABC đối đỉnh ⇒ ∠C'BA' = ∠ABC = 56°
Chọn đáp án D.
Bài 6: Chọn câu trả lời đúng. Góc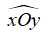 
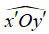
đối đỉnh với góc 
khi
A. Tia Ox’ là tia đối của tia Ox và tia Oy’ là tia đối của tia Oy
B. Tia Ox’ là tia đối của tia Oy và tia Ox là tia đối của tia Oy’
C. Tia Ox’ là tia đối của tia Ox và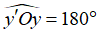 
D. Cả A, B, C đều đúng
TH1:
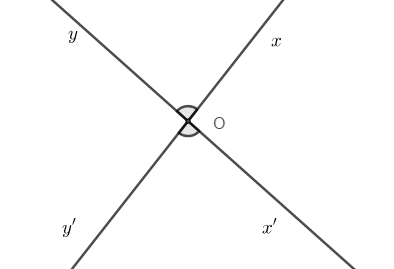
TH2:
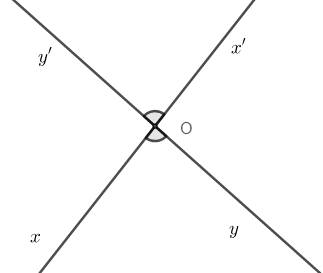
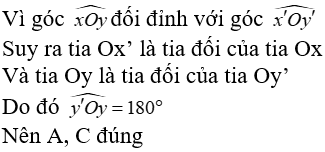
Vậy cả A, B, C đều đúng
Chọn đáp án D
Bài 7: Câu nào sau đây là sai:
A. Hai góc có mỗi cạnh của góc này là tia đối của mỗi cạnh của góc kia được gọi là hai góc đối đỉnh
B. Hai góc đối đỉnh thì bằng nhau
C. Hai góc bằng nhau thì đối đỉnh
D. Nếu số đo góc A bằng số đo của góc B và góc C đối đỉnh với B thì góc A và góc C bằng nhau
+ Ta có: A đúng (theo lý thuyết)
+ B Hai góc đối đỉnh thì bằng nhau là đúng (theo tính chất của hai góc đối đỉnh)
+ C Hai góc bằng nhau là hai góc đối đỉnh là sai
Ví dụ: Cho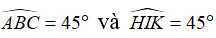 
và (các điểm A, B, C, H, I, K là các điểm phân biệt)
Chọn đáp án C
Bài 8: Hai tia phân giác của hai góc đối đỉnh là
A. Hai tia trùng nhau
B. Hai tia vuông góc
C. Hai tia đối nhau
D. Hai tia song song
Hai tia phân giác của hai góc đối đỉnh là hai tia đối nhau.
Thật vậy, ta chứng minh như sau:
Giả sử hai đường thẳng aa’ và bb’ cắt nhau tại O,
Như hình vẽ sau:
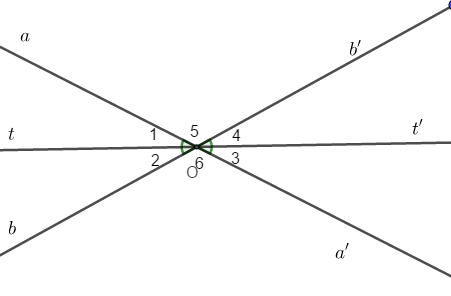
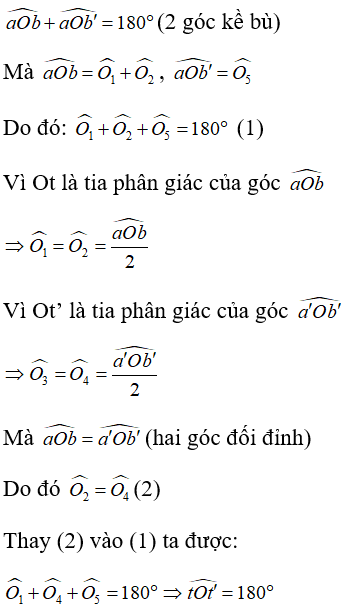
Suy ra Ot và Ot’ là hai tia đối nhau.
Chọn đáp án C
Bài 9: Chọn câu trả lời sai: Hai đường thẳng aa’ và bb’ cắt nhau tại K và góc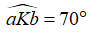 
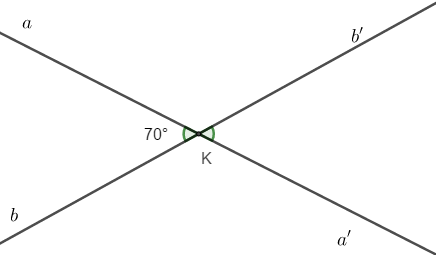
. Ta có:
Chọn đáp án C
Bài 10: Chọn câu phát biểu đúng
A. Hai đường thẳng cắt nhau tạo thành hai cặp góc đối đỉnh
B. Ba đường thẳng cắt nhau tạo thành ba cặp góc đối đỉnh
C. Bốn đường thẳng cắt nhau tạo thành bốn cặp góc đối đỉnh
D. Cả A, B, C đều đúng
A. Đúng (theo lý thuyết)
B. Sai
Phản ví dụ: Cho ba đường thẳng a, b, c cắt nhau như hình dưới đây
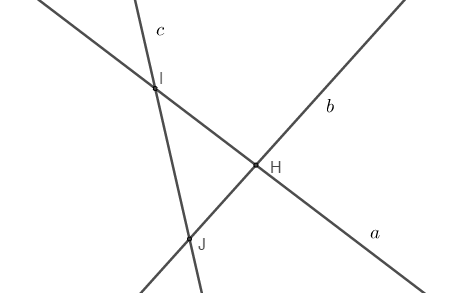
Ta thấy đường thẳng a cắt đường thẳng b tại điểm H, tạo ra 2 cặp góc đối đỉnh
Đường thẳng a cắt đường thẳng c tại điểm I, tạo ra 2 cặp góc đối đỉnh
Đường thẳng b cắt đường thẳng c tại điểm J, tạo ra 2 cặp góc đối đỉnh
Vậy ba đường thẳng a, b, c cắt nhau như hình vẽ trên có thể tạo ra 6 cặp góc đối đỉnh
Do đó B sai.
C. Sai. Tương tự câu B
D. Sai do B và C đều sai
Chọn đáp án A
Bài tập Hai đường thẳng vuông góc có lời giải
Bài 1: Chọn hai đường thẳng aa' và bb' vuông góc với nhau tại O. Hãy chỉ ra câu sai trong các câu sau:
A. ∠b'Oa' = 90°
B. ∠aOb = 90°
C. aa' và bb' không thể cắt nhau
D. aa' là đường phân giác của góc bẹt bOb'
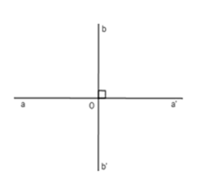
Hai đường thẳng và vuông góc với nhau tại nên:
+ ∠aOb = 90° nên B đúng.
+ aa' và bb' vuông góc với nhau nên aa' và bb' cắt nhau nên C sai.
+ ∠a'Ob = ∠ a'Ob' = 90° ⇒ aa' là đường phân giác của góc bẹt bOb' nên D đúng.
+ ∠b'Oa' = 90° nên A đúng.
Chọn đáp án C.
Bài 2: Hãy chọn câu đúng trong các câu sau:
A. Hai đường thẳng cắt nhau thì vuông góc
B. Hai đường thẳng vuông góc thì cắt nhau
C. Hai đường thẳng vuông góc thì trùng nhau
D. Cả ba đáp án A, B, C đều sai
Hai đường thẳng vuông góc thì cắt nhau
Chọn đáp án B.
Bài 3: Đường trung trực của một đoạn thẳng là:
A. Đường thẳng đi qua trung điểm của đoạn thẳng đó
B. Đường thẳng vuông góc với đoạn thẳng đó
C. Đường thẳng cắt đoạn thẳng đó
D. Đường thẳng vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó
Đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng ấy tại trung điểm của nó.
Chọn đáp án D.
Bài 4: Cho ∠AOB = 120°. Tia OC nằm giữa hai tia OA, OB sao cho ∠BOC = 30°. Chọn câu đúng:
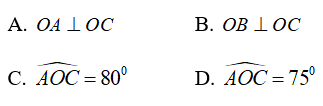
Vì OC nằm giữa hai tia OA, OB nên
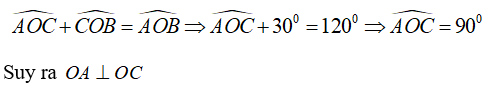
Chọn đáp án A.
Bài 5: Cho ∠AOB = 30°. Vẽ tia OC là tia đối của tia OA. Tính ∠COD biết OD vuông góc OB, các tia OD và OA thuộc hai nửa mặt phẳng đối nhau bờ OB
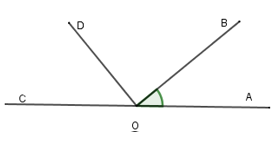
Vì OD vuông góc OB nên ∠DOB = 90°
Vì OA và OC là hai tia đối nhau và tia OB nằm giữa OA và OD nên ta có:
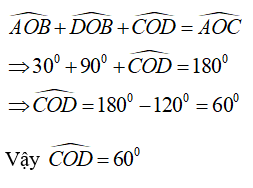
Chọn đáp án D.
Bài 6: Khi đường thẳng AB vuông góc với đường thẳng CD, ta kí hiệu:
A. AB // CD
B. AB = CD
C. AB CD
D. AB CD
Khi đường thẳng AB vuông góc với đường thẳng CD, ta kí hiệu AB ⊥ CD
Chọn đáp án D
Bài 7: Chọn phát biểu đúng
A. Có một và chỉ một đường thẳng d’ đi qua điểm O và vuông góc với đường thẳng d cho trước
B. Cho trước một điểm O và một đường thẳng d. Có một và chỉ một đường thẳng d’ đi qua O và vuông góc với d
C. Cả A và B đều đúng
D. Chỉ có B đúng
Tính chất thừa nhận: Có một và chỉ một đường thẳng d’ đi qua điểm O và vuông góc với đường thẳng d cho trước. (Phần lý thuyết)
Suy ra A đúng
B diễn đạt tương tự theo tính chất trên, nên đáp án B cũng đúng.
Vậy cả A và B đều đúng.
Chọn đáp án C
Bài 8: Cho đoạn thẳng MN = 6 cm. Trên tia MN lấy điểm P sao cho MP = 1 cm, trên tia NM lấy điểm Q sao cho NQ = 1 cm. Khi đó:
A. MQ = NP
B. Đường trung trực của đoạn thẳng MN vuông góc với đoạn thẳng PQ
C. Đường trung trực của đoạn thẳng MN trùng với đường trung trực của đoạn thẳng PQ
D. Cả A, B, C đều đúng
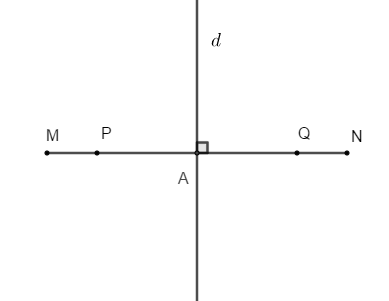
+ Trên tia MN có:
MN = 6 cm; MP = 1 cm
Suy ra P nằm giữa M và N (do 6 > 1)
⇒ MP + PN = MN ⇒ PN = MN – MP = 6 – 1 = 5 cm
+ Trên tia NM có:
NM = 6 cm; NQ = 1 cm
Suy ra Q nằm giữa M và N (do 6 > 1)
⇒ NQ + QM = NM ⇒ QM = NM – NQ = 6 – 1 = 5 cm
Do đó: PN = QM (= 5 cm) A đúng
+ Gọi A là trung điểm của đoạn thẳng MN ⇒ AM = AN = 1/2 MN = 3 cm
Gọi d là đường thẳng đi qua A và vuông góc với MN tại A
Do đó d là đường trung trực của đoạn thẳng MN
Vì P và Q đều thuộc MN, nên suy ra d ⊥ PQ (1) ⇒ B đúng
+ Trên tia MN có MA = 3 cm; MP = 1 cm
Suy ra P nằm giữa M và A ⇒ MP + PA = MA ⇒ PA = MA – MP = 3 – 1 = 2 cm
Chứng minh tương tự ta có: NQ + QA = NA ⇒ QA = NA – NQ = 3 – 1 = 2 cm
Do đó: PA = QA, mà P, Q, A thẳng hàng (do P, Q, A đều thuộc MN)
Suy ra A là trung điểm của PQ (2)
Từ (1) và (2) suy ra d là đường trung trực của đoạn thẳng PQ ⇒ C đúng
Chọn đáp án D
Bài 9: Cho hình vẽ sau, hãy chọn câu sai trong các câu sau
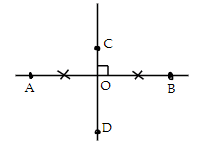
A. CD là đường trung trực của đoạn thẳng AB
B. AB là đường trung trực của đoạn thẳng CD
C.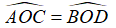 
D. AO = OB
Quan sát hình vẽ đã cho ta thấy
+ AO = OB (D đúng) ⇒ O là trung điểm của AB (1)
+ CD ⊥ AB tại O (2) ⇒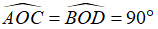 
⇒ C đúng
Từ (1) và (2) suy ra CD là đường trung trực của đoạn thẳng AB ⇒ A đúng
+ Vì OC ≠ OD suy ra AB không phải là đường trung trực của CD ⇒ B sai
Chọn đáp án B
Bài 10: Cho đường thẳng d và điểm O thuộc đường thẳng d. Vẽ đường thẳng d’ đi qua O và vuông góc với d. Chọn hình vẽ đúng trong các hình vẽ dưới đây.
A.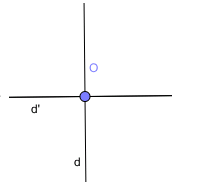 
B.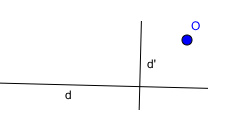 
C.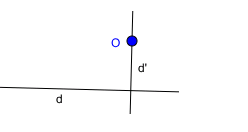 
D.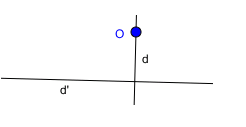 
Vì điểm O thuộc đường thẳng d, suy ra đáp án A và D thỏa mãn, loại B và C
Đường thẳng d’ đi qua O và vuông góc với d, suy ra A đúng, D sai
Chọn đáp án A
