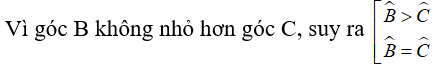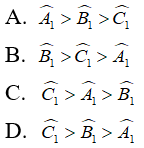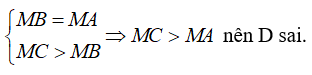200 Bài tập trắc nghiệm Toán lớp 7 Chương 3 Hình học có đáp án
200 Bài tập trắc nghiệm Toán lớp 7 Chương 3 Hình học có đáp án
Với bộ 200 Bài tập trắc nghiệm Toán lớp 7 Chương 3 Hình học có đáp án, chọn lọc sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 7.
- Bài tập Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài tập Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài tập Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Bài tập Tính chất ba đường trung tuyến của tam giác
- Bài tập Tính chất tia phân giác của một góc
- Bài tập Tính chất ba đường phân giác của tam giác
- Bài tập Tính chất đường trung trực của một đoạn thẳng
- Bài tập Tính chất ba đường trung trực của tam giác
- Bài tập Tính chất ba đường cao của tam giác
- Tổng hợp Trắc nghiệm Chương 2 Đại Số 7
Bài tập Quan hệ giữa góc và cạnh đối diện trong một tam giác có lời giải
Bài 1: Cho ΔABC có AC > BC > AB. Trong các khẳng định sau, câu nào đúng:
Vì ΔABC có AC > BC > AB nên theo quan hệ giữa cạnh và góc trong tam giác ta có: ∠C < ∠A < ∠B
Chọn đáp án C.
Bài 2: Cho tam giác có: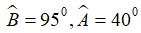
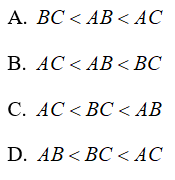
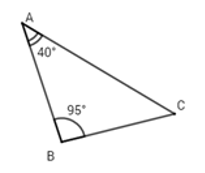
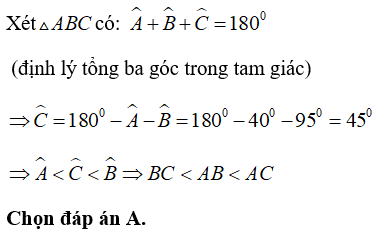
. Hãy chọn câu trả lời đúng nhất:
Bài 3: Ba cạnh của tam giác có độ dài là 6cm, 7cm, 8cm. Góc lớn nhất là góc:
A. Đối diện với cạnh có độ dài 6cm
B. Đối diện với cạnh có độ dài 7cm
C. Đối diện với cạnh có độ dài 8cm
D. Ba cạnh có độ dài bằng nhau
Vì trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn mà cạnh 8cm là cạnh lớn nhất trong tam giác nên góc lớn nhất là góc đối diện với cạnh có độ dài 8cm
Chọn đáp án C.
Bài 4: Cho ΔABC có AB + AC = 10cm; AC - AB = 4cm. So sánh ∠B và ∠C
Xét ΔABC có: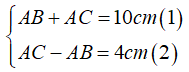
Từ (1) ⇒ AC = 10 - AB. Thế vào (2) ta được: 10 - AB - AB = 4 ⇒ 2AB = 6 ⇒ AB = 3 cm
⇒ AC = 10 - 3 = 7cm
Vì 3 < 7 nên AB < AC ⇒ C^ < B^ (trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn)
Chọn đáp án A.
Bài 5: Cho ΔABC có ∠A = 80°, ∠B - ∠C = 20°. Chọn câu trả lời đúng nhất:
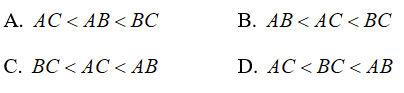
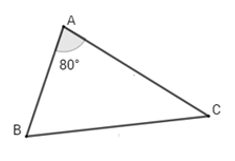
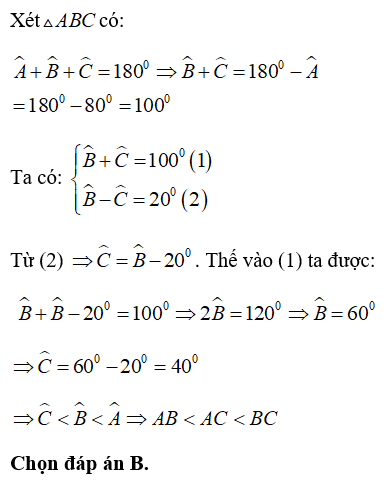
Bài 6: Cho tam giác ABC có A^ = 3C^ và B^ = 5C^. Chọn khẳng định đúng trong các khẳng định sau:
A. AB < AC < BC
B. AC < AB < BC
C. AB < BC < AC
D. BC < AC < AB
Chọn đáp án C
Bài 7: Cho tam giác ABC có C^ < B^ < 90°. Vẽ AH BC tại H, trên tia đối của tia HA lấy điểm D sao cho HA = HD. Câu nào sau đây sai?
A. AC > AB
B. DB > DC
C. DC > AB
D. AC > BD
Chọn đáp án B
Bài 8: Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại
D. Khi so sánh độ dài của AD và DC, khẳng định nào sau đây đúng?
A. AD < DC
B. AD = DC
C. AD > DC
D. Không so sánh được
Từ D kẻ đường thẳng vuông góc với BC cắt BC tại E
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD cạnh huyền chung
(BD là tia phân giác của góc B)
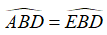
Khi đó: ΔABD = ΔEBD (cạnh huyền góc nhọn)
Suy ra: AD = DE (hai cạnh tương ứng) (1)
Lại có tam giác DEC vuông tại E có DC là cạnh huyền
Suy ra DC > DE (trong tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất) (2)
Từ (1) và (2) suy ra DC > AD hay AD < DC
Vậy A đúng, B, C, D sai.
Chọn đáp án A
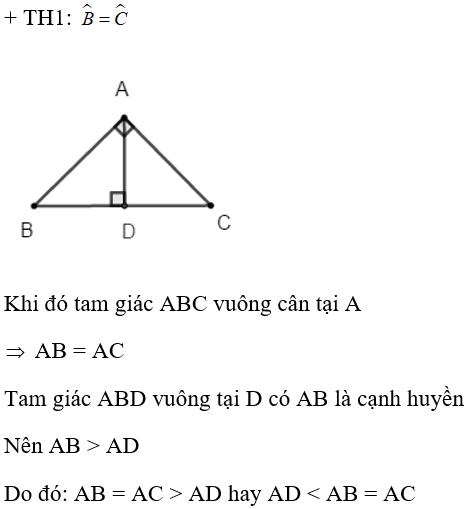
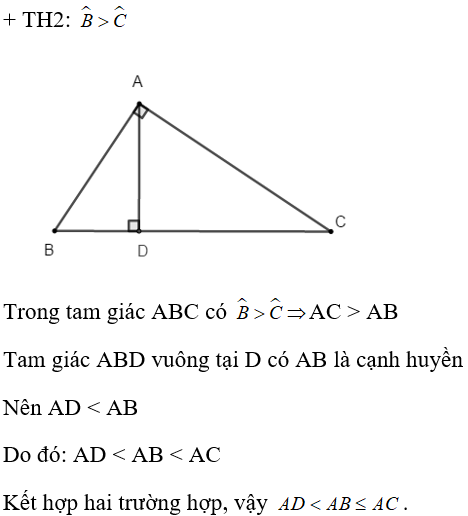
Bài 9: Cho tam giác ABC vuông tại A, có góc B không nhỏ hơn góc C và AD ⊥ BC tại D. Khi đó ta có:
A. AB < AC < AD
B. AB > AC > AD
C. AD < AB ≤AC
D. AD > AB ≥ AC
Chọn đáp án C
Bài 10: Tam giác ABC có AB = 5 cm; BC = 6 cm và AC = 7 cm. Gọi A1^; B1^; C1^ theo thứ tự là góc ngoài tại các đỉnh A, B, C của tam giác đó. Trong các khẳng định, khẳng định nào là đúng?
Chọn đáp án B
Bài tập Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu có lời giải
Bài 1: Chọn phát biểu sai trong các phát biểu sau:
A. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
B. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
C. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào lớn hơn có hình chiếu nhỏ hơn.
D. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
Trong các phát biểu, ý A, B, D đều đúng
Ý C sai vì: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào lớn hơn có hình chiếu lớn hơn.
Chọn đáp án C.
Bài 2: Cho ba điểm A, B, C thẳng hàng, B nằm giữa A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm H. Khi đó:
A. AH < BH B. AH < AB C. AH > BH D. AH = BH
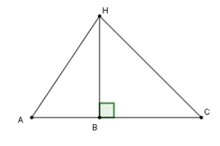
Vì BH là đường vuông góc và AH là đường xiên nên AH > BH
Chọn đáp án C.
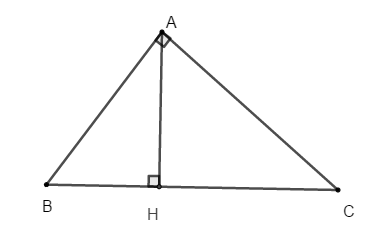
Bài 3: Trong tam giác ABC có chiều cao AH:
A. Nếu BH < HC thì AB < AC
B. Nếu AB < AC thì BH < HC
C. Nếu BH = HC thì AB = AC
D. Cả A, B, C đều đúng
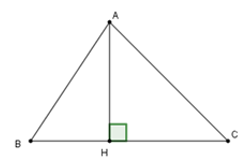
Trong tam giác ABC có AH là đường vuông góc và BH; CH lần lượt là hai hình chiếu của hai đường xiên AB và AC
Khi đó theo quan hệ giữa đường xiên và hình chiếu ta có
- Nếu BH < HC thì AB < AC
- Nếu AB < AC thì BH < HC
- Nếu BH = HC thì AB = AC
Nên cả A, B, C đều đúng.
Chọn đáp án D.
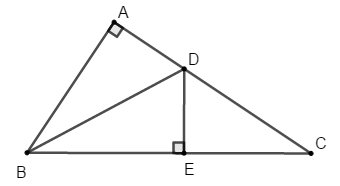
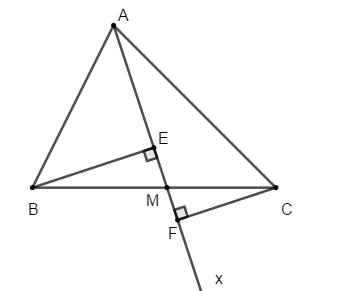
Bài 4: Cho hình vẽ sau:
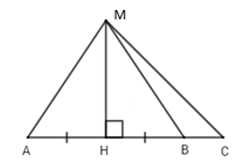
Chọn đáp án sai trong các đáp án sau:
A. MA > MH B. HB < HC C. MA = MB D. MC < MA
Vì MH là đường vuông góc và MA là đường xiên nên MA > MH (quan hệ đường vuông góc và đường xiên) nên A đúng.
Vì ∠MBC là góc ngoài ΔMHB ⇒ ∠MBC > ∠MHB = 90°
Xét ΔMBC có: ∠MBC là góc tù nên suy ra MC > MB (quan hệ giữa góc và cạnh trong tam giác)
Mà HB và HC lần lượt là hình chiếu của MB và MC trên AC.
⇒ HB < HC (quan hệ giữa đường xiên và hình chiếu) nên B đúng.
Vì AH = HB (gt) mà AH và HB lần lượt là hình chiếu của AM và BM .
⇒ MA = MB (quan hệ giữa đường xiên và hình chiếu) nên C đúng.
Ta có:
Chọn đáp án D.
Bài 5: Cho ΔABC vuông tại A, M là trung điểm của AC. Gọi D, E lần lượt là hình chiếu của A và C xuống đường thẳng BM. So sánh BD + BE và AB
A. BD + BE > 2AB
B. BD + BE < 2AB
C. BD + BE = 2AB
D. BD + BE < AB
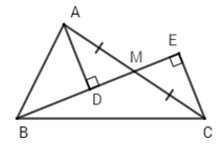
Vì ΔABM vuông tại A (gt) nên BA < BM (quan hệ giữa đường vuông góc và đường xiên)
Mà BM = BD + DM ⇒ BA < BD + DM (1)
Mặt khác: BM = BE - ME ⇒ BA < BE - ME (2)
Cộng hai vế của (1) và (2) ta được: 2BA < BD + BE + MD - ME (3)
Vì M là trung điểm của AC (gt) ⇒ AM = MC (tính chất trung điểm)
Xét tam giác vuông ADM và tam giác vuông CEM có:
AM = MC (cmt)
∠AMD = ∠EMC (đối đỉnh)
Do đó: ΔADM = ΔCEM (cạnh huyền – góc nhọn)
⇒ MD = ME (4) (2 cạnh tương ứng)
Từ (3) và (4) ⇒ BD + BE > 2AB
Chọn đáp án A.
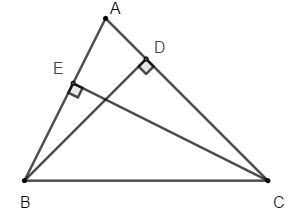
Bài 6: Cho tam giác ABC, có B^ = 2C^. Tia phân giác góc B cắt AC tại D. Từ D kẻ đường thẳng DE // BC (E ∈ AB). Câu nào sai?
A. BD = DC
B. AE = EB
C. EB = ED
D. Nếu ΔABC vuông tại B thì DA = DC = DB
Chọn đáp án B
Bài 7: Cho tam giác ABC nhọn. Vẽ tia Ax nằm trong góc BAC, Ax cắt BC ở M. Gọi E và F theo thứ tự là hình chiếu của B và C trên tia Ax. So sánh BE + CF với B
C.
A. BE + CF < BC
B. BE + CF > BC
C. BE + CF = BC
D. BE + CF = 2BC
Chọn đáp án A
Bài 8: Cho tam giác ABC vuông tại A. Từ A hạ AH ⊥ BC tại H. Khi đó ta có
A. AH > BC
B. AH = BC
C. AH < BC
D. AH = 2BC
Chọn đáp án C
Bài 9: Cho tam giác ABC có D và E lần lượt là hình chiếu của B và C lên AC và AB. Khi đó ta có:
A. BD + CE > AB + AC
B. BD + CE < AB + AC
C. BD + CE = AB + AC
D. BD + CE = 1/2 (AB + AC)
Chọn đáp án B
Bài 10: Cho đường thẳng d và điểm A không thuộc đường thẳng d. Chọn khẳng định sai.
A. Có duy nhất một đường vuông góc kẻ từ điểm A đến đường thẳng d.
B. Có vô số đường xiên kẻ từ điểm A đến đường thẳng d.
C. Có vô số đường vuông góc kẻ từ điểm A đến đường thẳng d.
D. Trong các đường xiên và đường vuông góc kẻ từ điểm A đến đường thẳng d, đường vuông góc là đường ngắn nhất.
+ Ta biết rằng có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước và có vô số đường thẳng đi qua một điểm cho trước và cắt một đường thẳng cho trước. Bởi vậy, có một đường vuông góc kẻ từ điểm A đến đường thẳng d và có vô số đường xiên kẻ từ điểm A đến đường thẳng d nên A, B đúng và C sai.
+ Đáp án D đúng vì theo định lý phần lý thuyết.
Chọn đáp án C
