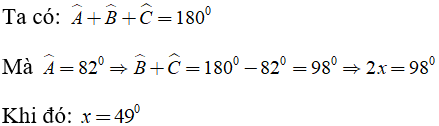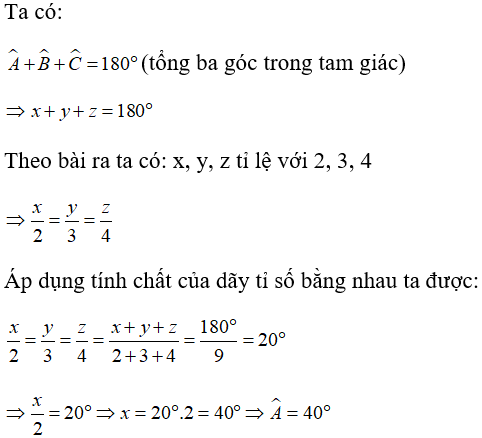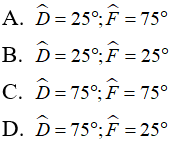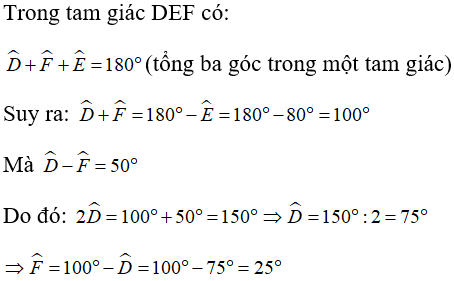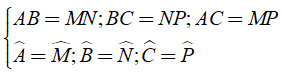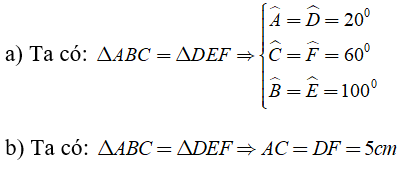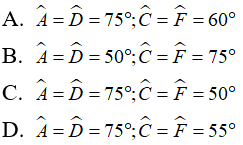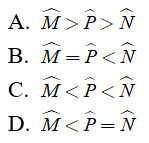200 Bài tập trắc nghiệm Toán lớp 7 Chương 2 Hình học có đáp án
200 Bài tập trắc nghiệm Toán lớp 7 Chương 2 Hình học có đáp án
Với bộ 200 Bài tập trắc nghiệm Toán lớp 7 Chương 2 Hình học có đáp án, chọn lọc sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 7.
- Bài tập Tổng ba góc của một tam giác
- Bài tập Hai tam giác bằng nhau
- Bài tập Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh (c.c.c)
- Bài tập Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c)
- Bài tập Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g.c.g)
- Bài tập Tam giác cân
- Bài tập Định lí Pi-ta-go
- Bài tập Các trường hợp bằng nhau của tam giác vuông
- Tổng hợp Trắc nghiệm Chương 2 Hình Học 7
Bài tập Tổng ba góc của một tam giác có lời giải
Bài 1: Tổng ba góc của một tam giác bằng?
A. 90° B. 180° C. 100° D. 120°
Tổng ba góc của một tam giác bằng 180°
Chọn đáp án B.
Bài 2: Cho tam giác ABC vuông tại A. Khi đó
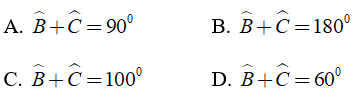
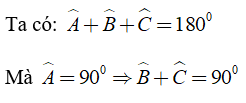
Chọn đáp án A.
Bài 3: Cho tam giác ABC có ∠A = 96°, ∠C = 50°. Số đo góc B là?
A. 34° B. 35° C. 60° D. 90°
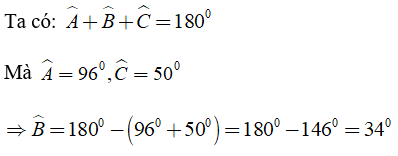
Chọn đáp án A.
Bài 4: Cho hình vẽ sau. Tính số đo x
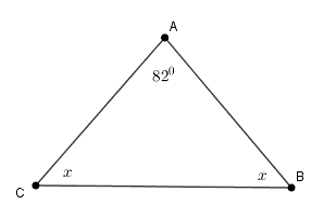
A. 40° B. 50° C. 49° D. 98°
Chọn đáp án C.
Bài 5: Một tam giác có số đo các góc bằng nhau. Tính các góc đó
A. 40° B. 50° C. 49° D. 60°
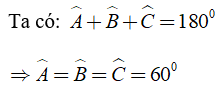
Chọn đáp án D.
Bài 6: Cho tam giác ABC, biết rằng số đo các góc tỉ lệ với 2, 3, 4. Số đo của góc A là:
A. 20°
B. 40°
C. 60°
D. 80°
Gọi số đo các góc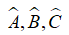 
của tam giác ABC lần lượt là x, y, z (Điều kiện: 0 < x, y, z < 180° )
Chọn đáp án B
Bài 7: Cho hình sau. Tính số đo góc x
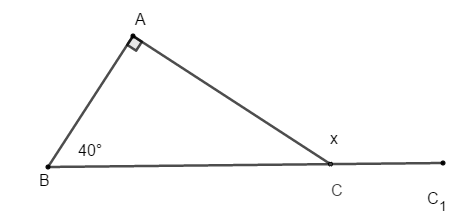
A. 130°
B. 140°
C. 50°
D. 40°
Chọn đáp án A
Bài 8: Cho một tam giác có hai góc bằng nhau và bằng 45°. Số đo góc còn lại là:
A. 45°
B. 85°
C. 90°
D. 180°
Chọn đáp án C
Bài 9: Cho tam giác DEF có D^ - F^ = 50° và E^ = 80°. Số đo của góc D^ và F^ lần lượt là?
Chọn đáp án D
Bài 10: Cho hình sau. Tính số đo góc x.
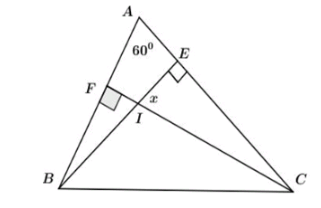
A. 40°
B. 50°
C. 60°
D. 70°
Chọn đáp án C
Bài tập Hai tam giác bằng nhau có lời giải
Bài 1: Cho ΔABC = ΔMNP. Chọn đáp án sai
A. AB = MN B. AC = NP C. ∠A = ∠M D. ∠P = ∠C
Ta có: ΔABC = ΔMNP ⇒
Vậy đáp án B sai.
Chọn đáp án B.
Bài 2: Cho ΔABC = ΔDEF. Biết ∠A = 33°, khi đó:
A. ∠D = 33° B. ∠D = 42° C. ∠E = 32° D. ∠D = 66°
Ta có: ΔABC = ΔDEF ⇒ ∠A = ∠D = 33°
Chọn đáp án A
Bài 3: Cho hai tam giác ABC và DEF có: AB = EF, BC = FD, AC = ED; ∠A = ∠E, ∠B = ∠F, ∠D = ∠C. Khi đó
A. ΔABC = ΔDEF
B. ΔABC = ΔEFD
C. ΔABC = ΔFDE
D. ΔABC = ΔDFE
Xét hai tam giác ABC và DEF có: AB = EF, BC = FD, AC = ED; ∠A = ∠E, ∠B = ∠F, ∠D = ∠C
Nên ΔABC = ΔEFD
Chọn đáp án B.
Bài 4: Cho ΔABC = ΔDEF, Biết ∠A = 32°, ∠F = 78°. Tính ∠B, ∠E
Vì ΔABC = ΔDEF nên ∠A = ∠D = 32°; ∠B = ∠E; ∠C = ∠F = 78°
Xét tam giác ABC có: ∠A + ∠B + ∠C = 180° ⇒ ∠B = 180° - (∠A + ∠C) = 180° - (32° + 78°) = 70°
Vậy ∠B = ∠E = 70°
Chọn đáp án D
Bài 5: Cho ΔABC = ΔMNP. Biết AB = 5cm, MP = 7cm và chu vi của tam giác ABC bằng 22cm. Tính các cạnh còn lại của mỗi tam giác?
A. NP = BC = 9cm
B. NP = BC = 11cm
C. NP = BC = 10cm
D. NP = 9cm; BC = 10cm
Vì ΔABC = ΔMNP nên AB = MN = 5cm; BC = NP; AC = MP = 7cm
Chu vi tam giác ABC: AB + AC + BC = 22 ⇒ BC = 22 - (AB + AC) = 22 - 12 = 10 (cm)
Chọn đáp án C.
Bài 6: Cho Δ ABC = ΔDEF. Biết A^ + B^ = 130° và E^ = 55° . Tính các góc A^; C^; D^; F^.
Chọn đáp án C
Bài 7: Cho ΔDEF = ΔMNP . Biết EF + FD = 10 cm, NP – MP = 2 cm. Tính độ dài cạnh FD.
A. 4 cm
B. 6 cm
C. 8 cm
D. 10 cm
Ta có: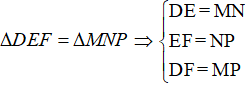 
Suy ra NP – MP = EF – DF = 2 cm
Mà EF + FD = 10 cm
Do đó: 2EF = 2 + 10 = 12
⇒EF = 12 : 2 = 6 cm
⇒FD = EF – 2 = 6 – 2 = 4 cm
Chọn đáp án A
Bài 8: Cho ΔABC = ΔMNP trong đó A^ = 30°; P^ = 60°. So sánh các góc
Chọn đáp án C
Bài 9: Cho ΔABC = ΔHIK. Biết HI = 5 cm, IK = 7 cm, chu vi tam giác ABC là 20 cm. Độ dài cạnh AC là?
A. AC = 5 cm
B. AC = 6 cm
C. AC = 7 cm
D. AC = 8 cm
Chọn đáp án D
Bài 10: Cho ΔABC = ΔHIK, biết A^ + H^ = 80°, I^ = 70°. Số đo góc C^ là:
Chọn đáp án D
