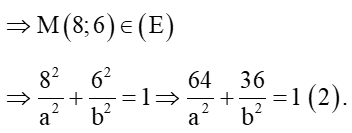Bài 4 trang 56 Chuyên đề Toán 10

Giải Chuyên đề Toán 10 Bài 2: Hypebol

Haylamdo biên soạn và sưu tầm lời giải Bài 4 trang 56 Chuyên đề Toán 10 trong Bài 2: Hypebol. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh biết cách làm bài tập Chuyên đề Toán 10.

Bài 4 trang 56 Chuyên đề Toán 10: Trong mặt phẳng tọa độ Oxy, cho hypebol $\left(H\right):\frac{x^2}{64}-\frac{y^2}{36}=1$. Lập phương trình chính tắc của elip (E), biết rằng (E) có các tiêu điểm là các tiêu điểm của (H) và các đỉnh của hình chữ nhật cơ sở của (H) đều nằm trên (E).

Lời giải:

Hypebol (H) có a = 8, b = 6 $\Rightarrow c=\sqrt{a^2+b^2}=10$ và một đỉnh của hình chữ nhật cơ sở là M(8; 6).

Gọi phương trình chính tắc của elip cần tìm là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).

Theo đề bài ta có:

+) (E) có các tiêu điểm là các tiêu điểm của (H)

$\Rightarrow c=10\Rightarrow a^2-b^2=c^2=100\left(1\right).$

+) Các đỉnh của hình chữ nhật cơ sở của (H) đều nằm trên (E)

Thế (1) vào (2) ta được:

Vậy phương trình chính tắc của elip cần tìm là $\frac{x^2}{160}+\frac{y^2}{60}=1.$