Bài 10 trang 23 Chuyên đề Toán 12 Chân trời sáng tạo

Một người muốn làm một thùng chứa hình trụ có nắp, có dung tích 500 dm. Cần chọn bán kính đáy và chiều cao của thùng bằng bao nhiêu để tiết kiệm nguyên liệu nhất? Biết đáy và mặt xung quanh của thùng có độ dày như nhau và xác định trước.

Giải Chuyên đề Toán 12 Bài tập cuối chuyên đề 1 - Chân trời sáng tạo

Bài 10 trang 23 Chuyên đề Toán 12: Một người muốn làm một thùng chứa hình trụ có nắp, có dung tích 500 dm³. Cần chọn bán kính đáy và chiều cao của thùng bằng bao nhiêu để tiết kiệm nguyên liệu nhất? Biết đáy và mặt xung quanh của thùng có độ dày như nhau và xác định trước.

Lời giải:

Bán kính và chiều cao của thùng chứa lần lượt là R và h (dm; R, h > 0).

Thể tích thùng chứa hình trụ là V = πR²h = 500 (dm³).

Suy ra $h=\frac{500}{\pi R^2}$(dm).

Để tiết kiệm nguyên liệu nhất thì diện tích toàn phần của thùng chứa phải nhỏ nhất.

Diện tích toàn phần của thùng chứa hình trụ là

S = 2πRh + 2πR² = $2\pi R\cdot \frac{500}{\pi R^2}+2\pi R^2$= $\frac{1000}{R}+2\pi R^2$(dm²).

Xét hàm số $S\left(R\right)=\frac{1000}{R}+2\pi R^2$ với R ∈ (0; + ∞).

Ta có $S^{\text{'}}\left(R\right)=4\pi R-\frac{1000}{R^2}$;

         $S^{\text{'}}\left(R\right)=0\iff 4\pi R-\frac{1000}{R^2}=0\iff 4\pi R^3=1000\iff R=\sqrt[3]{\frac{250}{\pi }}$ ∈ (0; + ∞).

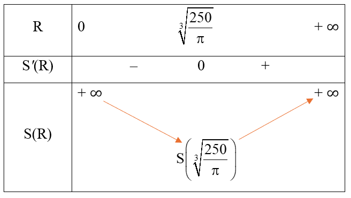
Bảng biến thiên:

Từ bảng biến thiên, ta có $\underset{\left(0;+\infty \right)}{\min }S\left(R\right)=S\left(\sqrt[3]{\frac{250}{\pi }}\right)$, đạt được tại $R=\sqrt[3]{\frac{250}{\pi }}$

Với $R=\sqrt[3]{\frac{250}{\pi }}$ thì ta có $h=2\sqrt{\frac{\pi }{250}}$.

Vậy với bán kính $R=\sqrt[3]{\frac{250}{\pi }}$(dm) và đường cao $h=2\sqrt{\frac{\pi }{250}}$(dm) thì tiết kiệm nguyên liệu làm thùng chứa nhất.

Lời giải bài tập Chuyên đề Toán 12 Bài tập cuối chuyên đề 1 hay, chi tiết khác:

• Bài 1 trang 21 Chuyên đề Toán 12: Giá trị lớn nhất của biểu thức F(x; y) = 5x – 2y trên miền Ω ở Hình 1 là ....

• Bài 2 trang 21 Chuyên đề Toán 12: Giá trị nhỏ nhất của biểu thức F(x; y) = 5x + 2y trên miền Ω ở Hình 2 là ....

• Bài 3 trang 22 Chuyên đề Toán 12: Một nhà phân phối có thể thuê tối đa 3 chiếc xe tải loại A ....

• Bài 4 trang 22 Chuyên đề Toán 12: Một người muốn làm một bể chứa hình hộp chữ nhật không nắp có thể tích 4 m³ ....

• Bài 5 trang 22 Chuyên đề Toán 12: Chi phí để sản xuất x sản phẩm là C(x) = 2 500 + 10x + $\frac{1}{4}{x}^2$ (nghìn đồng) ....

• Bài 6 trang 22 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính: F = 40x + 15y → max, min....

• Bài 7 trang 22 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính: F = 3x + 5y → min ....

• Bài 8 trang 22 Chuyên đề Toán 12: Thức ăn chăn nuôi A gồm 60% bột ngô và 40% bột đậu nành, thức ăn chăn nuôi B ....

• Bài 9 trang 23 Chuyên đề Toán 12: Hàm lượng protein, lipid và glucid (tính theo gam) trong 100 g mỗi loại thực phẩm A và B ....

• Bài 11 trang 23 Chuyên đề Toán 12: Cho mạch điện có sơ đồ như Hình 4. Nguồn điện có suất điện động E = 4 V ....

• Bài 12 trang 23 Chuyên đề Toán 12: Theo kết quả thăm dò trước một buổi biểu diễn văn nghệ ngoài trời, nếu giá bán mỗi vé là p ....