Bài 6 trang 22 Chuyên đề Toán 12 Chân trời sáng tạo

Giải bài toán quy hoạch tuyến tính: F = 40x + 15y → max, min với ràng buộc

Giải Chuyên đề Toán 12 Bài tập cuối chuyên đề 1 - Chân trời sáng tạo

Bài 6 trang 22 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính: F = 40x + 15y → max, min với ràng buộc $\left\{\begin{array}{l}5x+3y\le 15\\ x+3\le 3y\\ x\ge 0.\end{array}\right.$

Lời giải:

Viết lại ràng buộc của bài toán thành

$\left\{\begin{array}{l}5x+3y-15\le 0\\ x-3y+3\le 0\\ x\ge 0.\end{array}\right.$

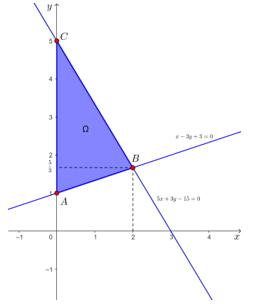
Tập phương án Ω của bài toán là miền tam giác ABC được tô màu như hình vẽ dưới đây.

Tọa độ giao điểm A của hai đường thẳng x = 0 và x – 3y + 3 = 0 là nghiệm của hệ phương trình $\left\{\begin{array}{l}x=0\\ x-3y+3=0\end{array}\right.\iff \left\{\begin{array}{l}x=0\\ y=1\end{array}\right.\Rightarrow A\left(0;1\right)$.

Tương tự, ta tìm được $B\left(2;\frac{5}{3}\right)$ và C(0; 5).

Giá trị của biểu thức F tại các đỉnh của Ω:

F(0; 1) = 40 ∙ 0 + 15 ∙ 1 = 15;

$F\left(2;\frac{5}{3}\right)=40\cdot 2+15\cdot \frac{5}{3}=105$; 

F(0; 5) = 40 ∙ 0 + 15 ∙ 5 = 75.

Từ đó, $\underset{\Omega }{\max }F=F\left(2;\frac{5}{3}\right)=105;\underset{\Omega }{\min }F=F\left(0;1\right)=15$.

Lời giải bài tập Chuyên đề Toán 12 Bài tập cuối chuyên đề 1 hay, chi tiết khác:

• Bài 1 trang 21 Chuyên đề Toán 12: Giá trị lớn nhất của biểu thức F(x; y) = 5x – 2y trên miền Ω ở Hình 1 là ....

• Bài 2 trang 21 Chuyên đề Toán 12: Giá trị nhỏ nhất của biểu thức F(x; y) = 5x + 2y trên miền Ω ở Hình 2 là ....

• Bài 3 trang 22 Chuyên đề Toán 12: Một nhà phân phối có thể thuê tối đa 3 chiếc xe tải loại A ....

• Bài 4 trang 22 Chuyên đề Toán 12: Một người muốn làm một bể chứa hình hộp chữ nhật không nắp có thể tích 4 m³ ....

• Bài 5 trang 22 Chuyên đề Toán 12: Chi phí để sản xuất x sản phẩm là C(x) = 2 500 + 10x + $\frac{1}{4}{x}^2$ (nghìn đồng) ....

• Bài 7 trang 22 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính: F = 3x + 5y → min ....

• Bài 8 trang 22 Chuyên đề Toán 12: Thức ăn chăn nuôi A gồm 60% bột ngô và 40% bột đậu nành, thức ăn chăn nuôi B ....

• Bài 9 trang 23 Chuyên đề Toán 12: Hàm lượng protein, lipid và glucid (tính theo gam) trong 100 g mỗi loại thực phẩm A và B ....

• Bài 10 trang 23 Chuyên đề Toán 12: Một người muốn làm một thùng chứa hình trụ có nắp, có dung tích 500 dm³ ....

• Bài 11 trang 23 Chuyên đề Toán 12: Cho mạch điện có sơ đồ như Hình 4. Nguồn điện có suất điện động E = 4 V ....

• Bài 12 trang 23 Chuyên đề Toán 12: Theo kết quả thăm dò trước một buổi biểu diễn văn nghệ ngoài trời, nếu giá bán mỗi vé là p ....