Bài 8 trang 22 Chuyên đề Toán 12 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

Thức ăn chăn nuôi A gồm 60% bột ngô và 40% bột đậu nành, thức ăn chăn nuôi B gồm 80% bột ngô và 20% bột đậu nành. Hiện tại xí nghiệp sản xuất chỉ còn 2,4 tấn bột ngô và 1,2 tấn bột đậu nành. Với số nguyên liệu này, xí nghiệp đó nên sản xuất khối lượng bao nhiêu mỗi loại sản phẩm A và B để thu được lợi nhuận cao nhất? Biết rằng A cho lợi nhuận 2 triệu đồng/tấn và B cho lợi nhuận 1,8 triệu đồng/tấn.

Giải Chuyên đề Toán 12 Bài tập cuối chuyên đề 1 - Chân trời sáng tạo

Bài 8 trang 22 Chuyên đề Toán 12: Thức ăn chăn nuôi A gồm 60% bột ngô và 40% bột đậu nành, thức ăn chăn nuôi B gồm 80% bột ngô và 20% bột đậu nành. Hiện tại xí nghiệp sản xuất chỉ còn 2,4 tấn bột ngô và 1,2 tấn bột đậu nành. Với số nguyên liệu này, xí nghiệp đó nên sản xuất khối lượng bao nhiêu mỗi loại sản phẩm A và B để thu được lợi nhuận cao nhất? Biết rằng A cho lợi nhuận 2 triệu đồng/tấn và B cho lợi nhuận 1,8 triệu đồng/tấn.

Lời giải:

Gọi x, y (x ≥ 0, y ≥ 0, tính theo tấn) lần lượt là khối lượng thức ăn chăn nuôi loại A và loại B mà xí nghiệp sản xuất.

Vì xí nghiệp sản xuất chỉ còn 2,4 tấn bột ngô và 1,2 tấn bột đậu nành nên ta có các bất phương trình

$\{\begin{cases} 0,6 x + 0,8 y \leq 2,4 \\ 0,4 x + 0,2 y \leq 1,2 \end{cases}$ hay $\{\begin{cases} 3 x + 4 y \leq 12 \\ 2 x + y \leq 6. \end{cases}$

Lợi nhuận của xí nghiệp thu được đối với hai loại sản phẩm A và B là

L = 2x + 1,8y (triệu đồng).

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

L = 2x + 1,8y → max

với ràng buộc

$\{\begin{cases} 3 x + 4 y \leq 12 \\ 2 x + y \leq 6 \\ x \geq 0 \\ y \geq 0. \end{cases}$

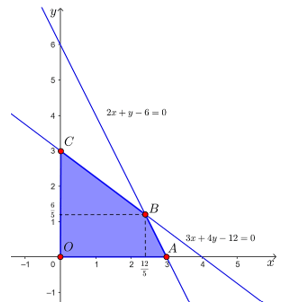
Tập phương án Ω của bài toán là miền tứ giác OABC được tô màu như hình dưới đây, có các đỉnh O(0; 0), A(3; 0), B $(\frac{12}{5}; \frac{6}{5})$ và C(0; 3).

Bài 8 trang 22 Chuyên đề Toán 12

Giá trị của L tại các đỉnh:

L(0; 0) = 0;

L(3; 0) = 2 ∙ 3 + 1,8 ∙ 0 = 6;

$L (\frac{12}{5}; \frac{6}{5}) = 2 \cdot \frac{12}{5} + 1,8 \cdot \frac{6}{5} = 6,96$ ;

L(0; 3) = 2 ∙ 0 + 1,8 ∙ 3 = 5,4.

Do đó, $\max_{Ω} L = 6,96$ , đạt được khi $x = \frac{12}{5} = 2,4; y = \frac{6}{5} = 1,2$ .

Vậy xí nghiệp đó nên sản xuất 2,4 tấn sản phẩm loại A và 1,2 tấn sản phẩm loại B thì thu được lợi nhuận cao nhất là 6,96 triệu đồng.

Lời giải bài tập Chuyên đề Toán 12 Bài tập cuối chuyên đề 1 hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯