Bài 9 trang 23 Chuyên đề Toán 12 Chân trời sáng tạo

Hàm lượng protein, lipid và glucid (tính theo gam) trong 100 g mỗi loại thực phẩm A và B được cho bởi bảng sau:

Giải Chuyên đề Toán 12 Bài tập cuối chuyên đề 1 - Chân trời sáng tạo

Bài 9 trang 23 Chuyên đề Toán 12: Hàm lượng protein, lipid và glucid (tính theo gam) trong 100 g mỗi loại thực phẩm A và B được cho bởi bảng sau:

Bài 9 trang 23 Chuyên đề Toán 12

Từ hai loại thực phẩm A và B, người ta muốn tạo ra một lượng thực phẩm chứa ít nhất 480 g protein, 90 g lipid và 2 400 g glucid. Biết rằng một kilôgam mỗi loại thực phẩm

A và B có giá lần lượt là 80 nghìn đồng, 100 nghìn đồng. Cần chọn bao nhiêu kilôgam mỗi loại thực phẩm A và B để chi phí thấp nhất?

Lời giải:

Gọi x, y (x ≥ 0, y ≥ 0, tính theo kg) lần lượt là khối lượng thực phẩm A và B cần dùng.

Vì lượng thực phẩm tạo ra chứa ít nhất 480 g protein, 90 g lipid và 2 400 g glucid nên ta có các bất phương trình sau

$\{\begin{cases} 240 x + 80 y \geq 480 \\ 30 x + 20 y \geq 90 \\ 600 x + 800 y \geq 2 400 \end{cases}$ hay $\{\begin{cases} 3 x + y \geq 6 \\ 3 x + 2 y \geq 9 \\ 3 x + 4 y \geq 12. \end{cases}$

Chi phí mua hai loại thực phẩm A và B là T = 80x + 100y (nghìn đồng).

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

T = 80x + 100y → min

với ràng buộc

$\{\begin{cases} 3 x + y \geq 6 \\ 3 x + 2 y \geq 9 \\ 3 x + 4 y \geq 12 \\ x \geq 0 \\ y \geq 0. \end{cases}$

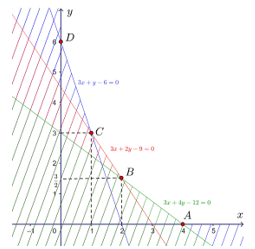
Tập phương án Ω của bài toán là miền không gạch chéo trên hình dưới đây, có các đỉnh A(4; 0), $B (2; \frac{3}{2})$ , C(1; 3) và D(0; 6).

Bài 9 trang 23 Chuyên đề Toán 12

Miền Ω nằm trong góc phần tư thứ nhất, các hệ số của hàm mục tiêu T dương nên T đạt giá trị nhỏ nhất tại đỉnh của Ω.

Giá trị của T tại các đỉnh:

T(4; 0) = 80 ∙ 4 + 100 ∙ 0 = 320;

$T (2; \frac{3}{2}) = 80 \cdot 2 + 100 \cdot \frac{3}{2} = 310$ ;

T(1; 3) = 80 ∙ 1 + 100 ∙ 3 = 380;

T(0; 6) = 80 ∙ 0 + 100 ∙ 6 = 600.

Suy ra $\min_{Ω} T = 310$ , đạt được khi x = 2; $y = \frac{3}{2} = 1,5$ .

Vậy cần mua 2 kg thực phẩm loại A và 1,5 kg thực phẩm loại B thì chi phí thấp nhất.

Lời giải bài tập Chuyên đề Toán 12 Bài tập cuối chuyên đề 1 hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯