Khám phá 1 trang 6 Chuyên đề Toán 12 Chân trời sáng tạo
Xét bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F = x + 2y với (x; y) là nghiệm của hệ bất phương trình (I)
Giải Chuyên đề Toán 12 Bài 1: Bài toán quy hoạch tuyến tính - Chân trời sáng tạo
Khám phá 1 trang 6 Chuyên đề Toán 12: Xét bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F = x + 2y với (x; y) là nghiệm của hệ bất phương trình (I)
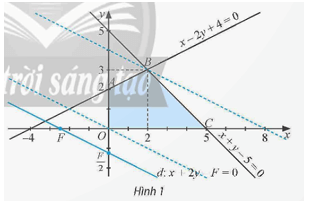
Miền nghiệm Ω của hệ (I) là miền tứ giác OABC (được tô màu) trên Hình 1. Với giá trị F cho trước, xét đường thẳng d: x + 2y – F = 0 hay .
Trả lời các câu hỏi sau để giải bài toán trên.
a) Với giá trị nào của F thì đường thẳng d đi qua điểm O, điểm B?
b) Khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của d với trục Oy thay đổi như thế nào? Khi đó, phương của đường thẳng d có thay đổi không?
c) Với điều kiện nào của F thì đường thẳng d và miền nghiệm Ω có điểm chung?
d) Từ đó, chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F = x + 2y trên miền nghiệm Ω. Biểu thức F đạt được các giá trị đó tại điểm nào?
Lời giải:
a)
● Đường thẳng d đi qua điểm O nên x = 0, y = 0, thay vào phương trình đường thẳng d ta được: 0 + 2 ∙ 0 – F = 0, suy ra F = 0.
● Đường thẳng d đi qua điểm B(2; 3) nên x = 2, y = 3, thay vào phương trình đường thẳng d ta được: 2 + 2 ∙ 3 – F = 0, suy ra F = 8.
b) Hoành độ giao điểm của d với trục Oy là x = 0, khi đó tung độ y = .
Khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của d với trục Oy cũng tăng (hoặc giảm).
Phương của đường thẳng d không thay đổi do không phụ thuộc vào F.
c) Đường thẳng d và miền nghiệm Ω có điểm chung khi 0 ≤ ≤ 4, tức là 0 ≤ F ≤ 8.
Vậy F ∈ [0; 8] thì đường thẳng d và miền nghiệm Ω có điểm chung.
d) Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F = x + 2y trên miền nghiệm Ω là , đạt được tại điểm B(2; 3).
Lời giải bài tập Chuyên đề Toán 12 Bài 1: Bài toán quy hoạch tuyến tính hay, chi tiết khác:
Khám phá 2 trang 8 Chuyên đề Toán 12: Xét bài toán quy hoạch tuyến tính F = 2x + y → max, min....
Thực hành 2 trang 10 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính: F = 25x + 10y → min ....
Vận dụng trang 10 Chuyên đề Toán 12: Cho bài toán quy hoạch tuyến tính F = 3x + 3y → max, min ....