Khám phá 3 trang 11 Chuyên đề Toán 12 Chân trời sáng tạo

Xét tình huống thương nhân thu mua trái cây ở Hoạt động khởi động (trang 6).

Giải Chuyên đề Toán 12 Bài 1: Bài toán quy hoạch tuyến tính - Chân trời sáng tạo

Khám phá 3 trang 11 Chuyên đề Toán 12: Xét tình huống thương nhân thu mua trái cây ở Hoạt động khởi động (trang 6).

a) Nếu gọi x, y (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua thì x và y phải thoả mãn hệ bất phương trình bậc nhất hai ẩn nào?

b) Từ đó, phát biểu bài toán quy hoạch tuyến tính tìm khối lượng thu mua mỗi loại trái cây để thu được lợi nhuận cao nhất. Giải bài toán đó.

Lời giải:

a) Vì x, y (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua nên x ≥ 0 và y ≥ 0.

Thương nhân mua tối đa 8 tấn trái cây nên x + y ≤ 8.

Số tiền mua x tấn trái cây loại A là 12x (triệu đồng).

Số tiền mua y tấn trái cây loại B là 20y (triệu đồng).

Vì tiền vốn là 120 triệu đồng nên 12x + 20y ≤ 120, tức là 3x + 5y ≤ 30.

Vậy x, y phải thỏa mãn hệ bất phương trình bậc nhất hai ẩn $\{\begin{cases} x + y \leq 8 \\ 3 x + 5 y \leq 30 \\ x \geq 0 \\ y \geq 0 \end{cases}$ .

b) Lợi nhuận thương nhân thu được là F = 1,1x + 1,5y (triệu đồng).

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

F = 1,1x + 1,5y → max

với ràng buộc

$\{\begin{cases} x + y \leq 8 \\ 3 x + 5 y \leq 30 \\ x \geq 0 \\ y \geq 0. \end{cases}$

Giải bài toán trên như sau:

Viết lại ràng buộc của bài toán thành $\{\begin{cases} x + y - 8 \leq 0 \\ 3 x + 5 y - 30 \leq 0 \\ x \geq 0 \\ y \geq 0. \end{cases}$

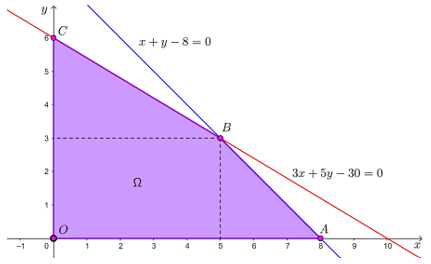
Tập phương án Ω của bài toán là miền tứ giác OABC như hình dưới đây với các đỉnh O(0; 0), A(8; 0), B(5; 3) và C(0; 6).

Khám phá 3 trang 11 Chuyên đề Toán 12

Giá trị của F tại các đỉnh:

F(0; 0) = 0;

F(8; 0) = 1,1 ∙ 8 + 1,5 ∙ 0 = 8,8;

F(5; 3) = 1,1 ∙ 5 + 1,5 ∙ 3 = 10;

F(0; 6) = 1,1 ∙ 0 + 1,5 ∙ 6 = 9.

Do đó, $\max_{Ω} F = 10$ , đạt được khi x = 5, y = 3.

Vậy thương nhân nên mua 5 tấn trái cây loại A và 3 tấn trái cây loại B thì thu được lợi nhuận cao nhất là 10 triệu đồng khi bán hết hàng đã thu mua.

Lời giải bài tập Chuyên đề Toán 12 Bài 1: Bài toán quy hoạch tuyến tính hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯