Thực hành 3 trang 13 Chuyên đề Toán 12 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

Một dây chuyền của nhà máy sản xuất đá xây dựng dự định sản xuất hai loại sản phẩm A và B. Thời gian để dây chuyền sản xuất 100 tấn sản phẩm loại A và 100 tấn sản phẩm loại B lần lượt là 2 giờ và 3 giờ. Do nhu cầu thị trường, xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B. Sản phẩm loại A cho lợi nhuận là 5 triệu đồng/100 tấn; sản phẩm loại B cho lợi nhuận 9 triệu đồng/100 tấn. Trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất bao nhiêu tấn sản phẩm loại A, bao nhiêu tấn sản phẩm loại B để thu được lợi nhuận cao nhất?

Giải Chuyên đề Toán 12 Bài 1: Bài toán quy hoạch tuyến tính - Chân trời sáng tạo

Thực hành 3 trang 13 Chuyên đề Toán 12: Một dây chuyền của nhà máy sản xuất đá xây dựng dự định sản xuất hai loại sản phẩm A và B. Thời gian để dây chuyền sản xuất 100 tấn sản phẩm loại A và 100 tấn sản phẩm loại B lần lượt là 2 giờ và 3 giờ. Do nhu cầu thị trường, xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B. Sản phẩm loại A cho lợi nhuận là 5 triệu đồng/100 tấn; sản phẩm loại B cho lợi nhuận 9 triệu đồng/100 tấn. Trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất bao nhiêu tấn sản phẩm loại A, bao nhiêu tấn sản phẩm loại B để thu được lợi nhuận cao nhất?

Lời giải:

Gọi x, y (x ≥ 0, y ≥ 0, tính theo tấn) lần lượt là khối lượng sản phẩm loại A và sản phẩm loại B cần sản xuất. Khi đó lợi nhuận thu được là P = 0,05x + 0,09y (triệu đồng).

Vì xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B nên x ≥ 3y.

Do thời gian để làm việc của dây chuyền không quá 6 giờ nên 0,02x + 0,03y ≤ 6.

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

P = 0,05x + 0,09y → max

với ràng buộc

$\{\begin{cases} x \geq 3 y \\ 0,02 x + 0,03 y \leq 6 \\ x \geq 0 \\ y \geq 0. \end{cases}$

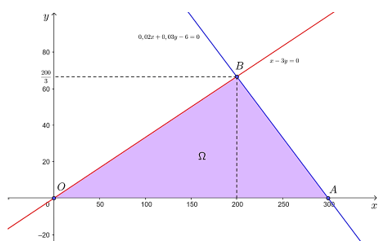
Tập phương án Ω của bài toán là miền tam giác OAB trên hình dưới đây với các đỉnh O(0; 0), A(300; 0) và $B (200; \frac{200}{3})$ .

Thực hành 3 trang 13 Chuyên đề Toán 12

Giá trị của P tại các đỉnh:

P(0; 0) = 0;

P(300; 0) = 0,05 ∙ 300 + 0,09 ∙ 0 = 15;

$P (200; \frac{200}{3}) = 0,05 \cdot 200 + 0,09 \cdot \frac{200}{3} = 16$ .

Do đó, $\max_{Ω} P = 16$ , đạt được khi x = 200, $y = \frac{200}{3} .$

Vậy trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất 200 tấn sản phẩm loại A và $\frac{200}{3}$ tấn sản phẩm loại B để thu được lợi nhuận cao nhất.

Lời giải bài tập Chuyên đề Toán 12 Bài 1: Bài toán quy hoạch tuyến tính hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯