Đề thi Giữa học kì 1 Toán lớp 8 Đà Nẵng năm 2024 (5 đề)

---

Đề thi Giữa học kì 1 Toán lớp 8 Đà Nẵng năm 2024 (5 đề)

Haylamdo biên soạn và sưu tầm Đề thi Giữa học kì 1 Toán lớp 8 Đà Nẵng năm 2024 (5 đề) được tổng hợp chọn lọc từ đề thi môn Toán 8 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 8.

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Đà Nẵng

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 1)

Câu 1: (2 điểm) Rút gọn biểu thức:

a. x(x + 2) -2x b. (2 + x)(2 - x) + x²

c. x²( 1- x) +( x+ 3)(x² - 3x + 9) d. (2x + y)² + 4x² - 4x( 2x+ y)

Câu 2: (2,0 điểm) Phân tích đa thức thành nhân tử:

a. 5xy -10 b. x² -36

c. x³ - x²y + 4x -4y d. x² + 12y -y² -36

Câu 3: (2,0 điểm) Tìm x biết:

a. 3(x + 1) + 5x =0 b. x² - 5x= 0

c. 4x² -1 -( 2x +1) d. x² -7x + 10 =0

Câu 4: (3,5 điểm) Cho tam giác ABC cân tại A (∠A < 90^o). Gọi M, N lần lượt là trung điểm của AB và Ac.

a. Tính MN biết BC = 7 cm.

b. Chứng minh rằng tứ giác MNCB là hình thang cân.

c. Kẻ MI vuông góc với BN tại I (I ∈ BN) và CK vuông góc với BN tại K (K ∈ BN). Chứng minh rằng: CK = 2MI.

d. Kẻ BD vuông góc với MC tại D (D ∈ MC). Chứng minh rằng DK // BC.

Câu 5: (0,5 điểm) Tìm giá trị lớn nhất của biểu thức:

A = 7 -x² - 3x

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Đà Nẵng

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 2)

Câu 1: (2 điểm) Phân tích đa thức thành nhân tử

a) 36a⁴- y²

b) 9x²y + 15xy² -3x

c) 6x² + x- 2

d) x² + 4xy - 4z² + 4y²

Câu 2: ( 1,5 điểm) Tìm x

a) (2x + 1)² -4x(x+3) = 9

b) x² - 12x= -36

c) (x² + 2x)² -2x² -4x = 3

Câu 3: (2,5 điểm)

1) Thực hiện phép tính

a) 2x(3x² -4x +2)

b) 2x(3x +5) -3( 2x² -2x + 3)

2) Tính giá trị biểu thức

A= x² - 6xy + 9y² -15 tại x = 37; y = - 1.

Câu 4: (3,5 điểm)

Cho hình bình hành ABCD, trên tia đối của tia AD lấy điểm E sao cho AE = AD.

Gọi F là giao điểm của EC và AB.

a. Chứng minh tứ giác AEBC là hình bình hành.

b. Chứng minh FE = FC.

c. Trên tia đối của tia CD lấy điểm M sao cho MC = CD. Chứng minh ba điểm E, B, M thẳng hàng.

Câu 5: (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức sau:

A= x² + y² + z² -yz -4x -3y + 2027

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Đà Nẵng

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 3)

Câu 1: (2 điểm) Phân tích đa thức thành nhân tử:

a) x² (x - y) + 2x -2y

b) (5x - 2y)(5x +2y) + 4y -1

c) x² (xy+ 1) + 2y -x -3xy

Câu 2: (1,5 điểm) Tìm x:

a) x(2x - 3) -2(3 -2x) = 0

b) (x +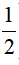)² - ( x +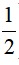)(x + 6) = 8

c) (x² +2x)² -2x² -4x = 8

Câu 3: (2,5 điểm)

a)Thực hiện phép tính rồi tính giá trị biểu thức:

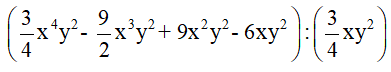tại x = 1 và y = 2020

b) Chứng minh biểu thức P = 2x² + y² -4x -4y + 10 luôn nhận giá trị dương với mọi biến x, y.

Câu 4: (3 điểm) Cho tam giác ABC nhọn, các đường cao AD và BE cắt nhau tại H. Gọi M là trung điểm của BC. Điểm P đối xứng với điểm H qua đường thẳng BC. Điểm Q đối xứng với điểm H qua điểm M.

a) Chứng minh PQ // BC. Khi đó tứ giác DMQP là hình gì? Vì sao?

b) Chứng minh tứ giác HCQB là hình bình hành. Tính số đo các góc .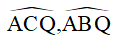

c) Gọi O là giao điểm các đường trung trực của . Chứng minh rằng điểm O cách đều 5 điểm A, B, P, Q, C.

Câu 5: (1 điểm) Tìm giá trj nhỏ nhất của biểu thức:

P = (x² + 4x + 1)² -12(x + 2)² + 2093

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Đà Nẵng

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 4)

Câu 1: (2 điểm) Phân tích đa thức thành nhân tử

a) 2x² -3x - 2 b) 4x(x - 2) + 3(2-x)

c) 27x³ + 8 d) x² + 2x -y² + 1

Câu 2: (2 điểm) Tìm x

a) 9x² + 6x - 3 =0

b) x(x - 2)(x + 2) - (x + 2)(x² - 2x + 4)=4

Câu 3:( (2 điểm) Rút gọn biểu thức và tính giá trị:

a) A= x(x + y) - 5(x+y) với x = 1; y = 2

b) B= 3x(x² - 3) + x²(4-3x) - 4x² với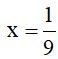

Câu 4: (3,5 điểm) Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Lấy một điểm E nằm giữa hai điểm O và B. Gọi F là điểm đối xứng với điểm A qua E và I là trung điểm của CF.

a) Chứng minh tứ giác OEFC là hình thang và tứ giác OEIC là hình bình hành.

b) Gọi H và K lần lượt là hình chiếu của F trên các đường thẳng BC và CD. Chứng minh tứ giác CHFK là hình chữ nhật.

c) Chứng minh bốn điểm E, H, K, I thẳng hàng.

Câu 5: (0,5 điểm) Tìm GTLN của biểu thức:

A= 5 + 2xy + 14y - x² -5y² - 2x

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Đà Nẵng

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 5)

Câu 1: (2 điểm) Phân tích đa thức sau thành nhân tử:

a) x² -3x + 2

b) x² + 4y² -4xy - 4

c) x² -y² -6y -9

Câu 2: (2 điểm) Tìm x

a) x( x - 3) -2x +6 = 0

b) 4x² - 25 (2x + 5)² =0

c) (x - 2)³ + (2x + 1)³ - 9(x+ 1)³ =-16

Câu 3: (2 điểm) Cho hai biểu thức

A = x² - x + 5 và B= ( x- 1)( x + 2) - x(x - 2) -3x

a) Tính giá trị của biểu thức A khi x = 2.

b) Chứng tỏ rằng B = - 2 với mọi giá trị của biến x.

c) Tìm giá trị nhỏ nhất của biểu thức C = A + B.

Câu 4: (0,5 điểm) Cho có E là trung điểm của Ac. Qua E kẻ ED // AB; (D ∈ BC); EF // BC (F ∈ AB)

a) Chứng minh rằng tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.

b) Gọi H là điểm đối xứng của D qua F. Chứng minh rằng HB // AD.

c) Gọi I là trung điểm của HB; K là giao điểm của AD và EF. Chứng minh rằng I, K, E thẳng hàng.

d) ∆ ABC cần có thêm điều kiện gì để HF =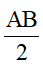

Câu 5: (0,5 điểm)

Tìm các cặp số (x; y) biết: y⁴ + y² + x² -8y -4x + 2xy + 7= 0