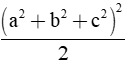Đề thi Học kì 1 Toán lớp 8 có đáp án (15 đề) năm 2024
Đề thi Học kì 1 Toán lớp 8 có đáp án (15 đề) năm 2024
Haylamdo biên soạn và sưu tầm Đề thi Học kì 1 Toán lớp 8 có đáp án (6 đề) được tổng hợp chọn lọc từ đề thi môn Toán 8 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 8.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 1)
I. Trắc nghiệm (3 điểm) Hãy chọn và ghi lại chữ cái đứng trước câu trả lời đúng vào bài làm
Câu 1. Số dư khi chia đa thức x2 + 2x + 3 cho đa thức x + 1 là:
A. – 2 B. 1 C. 2 D. 0
Câu 2. Khẳng định nào sau đây là sai?
A. Hình thang có hai cạnh bên bằng nhau là hình thang cân.
B. Hai tam giác bằng nhau có diện tích bằng nhau.
C. Tứ giác có các cạnh đối song song là hình bình hành.
D. Hình thoi có một góc vuông là hình vuông.
Câu 3. Kết quả của phép tính 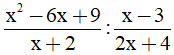 là:
là:
A. 2x – 6 B. x – 3 C. 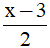 D. 6 – 2x
D. 6 – 2x
Câu 4. Giá trị của phân thức 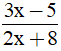 được xác định khi:
được xác định khi:
A. x ≠ 4 B. x ≠ 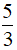 C. x ≠ -4 D. x ≠ -
C. x ≠ -4 D. x ≠ -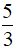
Câu 5. Hình nào dưới đây không có trục đối xứng:
A. Hình thoi B. Hình vuông C. Hình chữ nhật D. Hình bình hành
Câu 6. Giá trị lớn nhất của 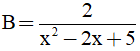 là:
là:
A. 2 B. 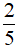 C. 4 D.
C. 4 D. 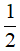
II. Tự luận (7 điểm)
Bài 1. (2 điểm) Cho biểu thức A = 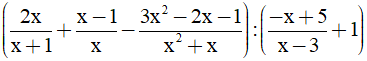
a) Tìm điều kiện xác định của A. Chứng tỏ 
b) Tính giá trị của A biết |x + 2| = 1.
c) Tìm x để 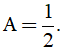
Câu 2: (1,5 điểm) Tìm x, biết:
a) 5x(x - 3) - x2 + 9 = 0
b) x + 4x2 + 4x3 = 0
c) 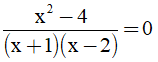
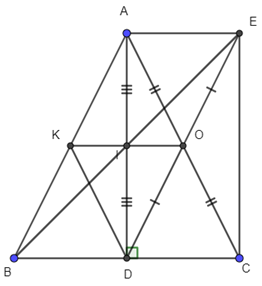
Bài 3: (3,5 điểm) Cho tam giác ABC cân tại A, đường cao AD, O là trung điểm của AC, điểm E đối xứng với điểm D qua điểm O.
a) Chứng minh tứ giác AECD là hình chữ nhật.
b) Gọi I là trung điểm của AD, chứng tỏ I là trung điểm của BE.
c) Cho AB = 10 cm, BC = 12 cm. Tính diện tích tam giác OAD.
d) Đường thẳng OI cắt AB tại K. Tìm điều kiện của tam giác ABC để tứ giác AEDK là hình thang cân.
ĐÁP ÁN VÀ BIỂU ĐIỂM CHI TIẾT
Câu |
Đáp án |
Biểu điểm |
Phần I. Trắc nghiệm | ||
|
(Mỗi câu đúng được 0,5 điểm) 1 – C; 2 – A; 3 – A; 4 – C; 5 – D; 6 – D. |
||
Phần II. Tự luận | ||
|
1 (2,0 đ) |
a) Điều kiện xác định: x2 + x ≠ 0 ⇔ x(x + 1) ≠ 0 ⇔
|
0,25 đ 0,5đ 0,25 đ |
|
b) Ta có |x + 2| = 1 ⇔ Thay x = -3 (TMĐK) vào A, ta được:
|
0,5đ 0,25đ |
|
|
c) Xét A =
⇔ 2(x - 3) = x + 1 ⇔ 2x - 6 = x + 1 ⇔ 2x - x = 1 + 6 ⇔ x = 7 |
0,25đ |
|
|
2 (1,5 đ) |
a) 5x(x - 3) - x2 + 9 = 0 ⇔ 5x(x - 3) - (x2 - 9) = 0 ⇔ 5x(x - 3) - (x - 3)(x + 3) = 0 ⇔ (x - 3)(5x - x - 3) = 0 ⇔ (x - 3)(4x - 3) = 0
Vậy x ∈ |
0,25đ 0,25đ |
|
b) x + 4x2 + 4x3 = 0 ⇔ x(1 + 4x + 4x2) = 0 ⇔ x(4x2 + 4x + 1) = 0 ⇔ x(2x + 1)2 = 0
Vậy x ∈ |
0,25đ 0,25đ |
|
|
c) Điều kiện xác định: (x + 1)(x - 2) ≠ 0 ⇔
⇔ x + 2 = 0 ⇔ x = -2 (TMĐK) Vậy x = -2. |
0,25đ 0,25đ |
|
|
3 (3,5 đ) |
- Vẽ đúng hình
(Nếu HS vẽ chưa hoàn chỉnh thì cho 0,25đ) |
0,5đ |
|
a) Xét tứ giác AECD, có: Hai đường chéo AC và DE cắt nhau tại O O là trung điểm của AC (gt) O là trung điểm của DE (E đối xứng với D qua O) Suy ra tứ giác AECD là hình bình hành. Ta lại có AD ⊥ BC ⇒ ∠ADC = 900 ⇒ AECD là hình chữ nhật. |
0,25đ 0,5 đ 0,5 đ |
|
|
b) Vì AECD là hình chữ nhật nên AD = CD và AD // CD hay AD // BD. Xét ΔABC cân tại A, có AD là đường cao nên AD cũng là đường là đường trung tuyến ⇒ D là trung điểm của BC. ⇒ BD = DC Mà AD = DC ⇒ AD = DB Xét ABDE có AD = DB và AD // BD nên ABDE là hình bình hành Mặt khác I là trung điểm AD Do đó I là trung điểm của BE. |
0,5đ 0,5đ |
|
|
c) Ta có: BD = DC = Xét tam giác ADC có: O là trung điểm AC I là trung điểm của AD ⇒ OI là đường trung bình tam giác ADC ⇒ OI // DC và Mà DC ⊥ AD(gt) ⇒ OI ⊥ AD Xét ΔABD vuông tại D, có: AB2 = AD2 + DB2 (định lý Py – ta – go) 102 = AD2 + 62 100 = AD2 + 36 AD2 = 100 – 36 AD2 = 64 AD = 8 cm. Diện tích tam giác OAD là:
|
0,25đ 0,25đ |
|
|
d) Ta có ABDE là hình bình hành nên AB // DE hay AK // DE Suy ra AKDE là hình thang. Nên để AKDE là hình thang cân thì ∠AED = ∠KDE (hai góc kề một đáy bằng nhau) Mà ∠AED = ∠ABD (hai góc đối trong hình bình hành ABDE) Tứ giác AODK có hình bình hành nên ∠KAO = ∠KDE ⇒ ∠KAO = ∠ABC⇒ ΔABCđều. |
0,25 đ 0,25 đ |
|
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 2)
Bài 1. (2 điểm) Phân tích đa thức thành nhân tử:
a) x2 - 4y2 - 2x + 4y b) (x2 + 2x)(x2 + 2x - 2) - 3
Bài 2. (0,5 điểm): Cho x + 2y = 5. Tính giá trị của biểu thức
A = x2 + 4y2 - 2x + 10 + 4xy - 4y
Bài 3. (2 điểm): Cho 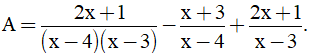
a) Rút gọn biểu thức A.
b) Tính giá trị của biểu thức A biết x2 = 9.
c) Tìm giá trị nhỏ nhất của B biết B = A.(x2 – 5x + 4).
Bài 4. (2 điểm): a) Tìm đa thức thương và đa thức dư trong phép chia sau:
(2x3 – 7x2 + 13x + 2) : (2x – 1).
b) Xác định số hữu tỉ a để f(x) = x3 – 2x2 + 5x + a chia hết cho đa thức g(x) = x – 3.
Bài 5. (3 điểm) Cho hình thoi ABCD có góc A bằng 600, kẻ BH vuông góc với AD tại H. Gọi O là giao điểm của AC và BD; E là điểm đối xứng của B qua H; F là điểm đối xứng của C qua B.
a) Tứ giác ABDE là hình gì? Vì sao?
b) Chứng minh tứ giác ABCE là hình thang cân.
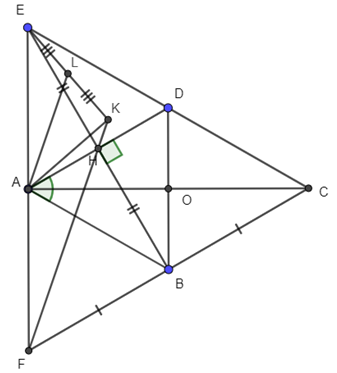
c) Kẻ AK ⊥ OE tại K. Gọi L là trung điểm của đoạn EK. Chứng minh AL // FK.
Bài 6. (0,5 điểm) Tìm tất cả các tam giác vuông có số đo các cạnh là các số nguyên dương và số đo diện tích bằng số đo chu vi.
ĐÁP ÁN VÀ BIỂU ĐIỂM CHI TIẾT
Câu |
Đáp án |
Biểu điểm |
|
Bài 1 (1,0 đ) |
a) x2 - 4y2 2x + 4y = (x2 - 2x + 1) - (4y2 - 4y + 1) = (x - 1)2 - (2y - 1)2 = (x - 1 + 2y - 1)(x - 1 - 2y + 1) = (x + 2y - 2)(x - 2y) |
0,25 đ 0,25 đ |
|
b) (x2 + 2x)(x2 + 2x - 2) - 3 = [(x2 + 2x - 1) + 1][(x2 + 2x - 1) - 1] - 3 = (x2 + 2x - 1)2 - 22 = (x2 + 2x + 1)(x2 + 2x - 3) = (x + 1)2 (x - 1)(x + 3) |
0,25đ 0,25đ |
|
|
Bài 2 (0,5 đ) |
Ta có: = (x2 + 4xy + 4y2) + (-2x – 4y) + 10 = (x + 2y)2 – 2(x + 2y) + 10 Thay x + 2y = 5 vào biểu thức A, ta có: A= 52 – 2.5 + 10 = 25 – 10 + 10 = 25. Vậy với x + 2y = 5 thì A = 25. |
0,25đ 0,25đ |
|
Bài 3 (2,0 đ) |
a) Điều kiện xác định:
|
0,25đ 0,25đ 0,25 0,25đ |
|
b) Ta có x2 = 9 x = 3 (Loại) hoặc x = - 3 (TMĐK) Thay x = - 3 (TMĐK) vào biểu thức A, ta được:
Vậy giá trị của biểu thức A là |
0,25đ 0,25đ |
|
|
c) Ta có: B = A.(x2 – 5x + 4)
= (x – 2)(x – 1) = x2 – 3x + 2
Vì
Dấu “ = “ xảy ra khi Vậy giá trị nhỏ nhất của biểu thức B là |
0,25đ 0,25đ |
|
|
3 (2, 0 đ) |
a) Đặt tính:
Vậy đa thức thương là x2 – 3x + 5 và đa thức dư là 7. |
0,5đ 0,5 đ |
|
b) Đặt tính:
Để đa thức f(x) chia hết cho đa thức g(x) thì a + 24 = 0 ⇔ a = -24. Vậy với a = -24 thì đa thức f(x) chia hết cho đa thức g(x). |
0,5đ 0,25đ 0,25đ |
|
|
5 (3,0 đ) |
- Vẽ đúng hình
(Nếu HS vẽ chưa hoàn chỉnh thì cho 0,25đ) |
0,5đ |
|
a) Xét tam giác ABD có AB = AD (do ABCD là hình thoi) Suy ra ΔABD cân Mà ∠BAD = 600 nên ΔABD đều Ta lại có BH là đường cao nên BH cũng là đường trung tuyến của ΔABD. ⇒ H là trung điểm của AD. Xét tứ giác ABDE có hai đường chéo AD và BE cắt nhau tại H H là trung điểm của BE (do B và E đối xứng với nhau qua H) H là trung điểm của AD (cmt) Do đó ABDE là hình bình hành Mà AD ⊥ BE tại H (gt). ⇒ ABDE là hình thoi. |
0,25đ 0,25đ 0,25đ 0,25đ |
|
|
b) Ta có DE // AB (ABDE là hình thoi) và DC // AB (ABCD là hình thoi) nên ED, DC trùng nhau ⇒ E, D, C thẳng hàng Xét tứ giác ABCE có AB // DE nên tứ giác ABCE là hình thang (1) Ta có: ∠BAD = ∠BCD = 600 (hai góc đối trong hình thoi ABCD) Do tam giác ABD đều nên AB = BD = AD = AE = DE Suy ra tam giác AED đều ⇒ ∠AED = 600 ⇒ ∠AED = ∠BCD (= 600) (2) Từ (1) và (2) suy ra ABCE là hình thang cân. |
0,25đ 0,25đ 0,25đ 0,25đ |
|
|
c) Vì ABCD là hình thoi có hai đường chéo AC giao BD tại O nên O là trung điểm của AC Xét tam giác ACF có: O là trung điểm của AC (cmt) B là trung điểm của CF (C và F đối xứng với nhau qua B) Suy ra OB là đường trung bình của tam giác ACF. ⇒ OB // AF Mà BD // AE (ABDE là hình thoi) Do đó AF trùng với AE hay A, F, E thẳng hàng. Xét ΔCFE, có : D là trung điểm của CE AD // EF Suy ra A là trung điểm của EF. Xét ΔKFE, có : L là trung điểm của KE (gt) A là trung điểm của EF (cmt) ⇒ AL là đường trung bình của tam giác FKE. ⇒ AL // FK |
0,25đ 0,25đ |
|
|
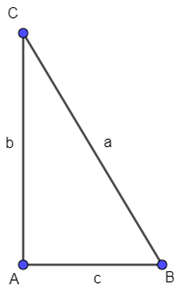
Giả sử tam giác vuông ABC có độ dài các cạnh như hình vẽ thỏa mãn yêu cầu đầu bài.
Khi đó, ta có: a, b, c là các số nguyên dương và 1 ≤ b ≤ c < a . Diện tích tam giác ABC là: Chu vi tam giác ABC là: a + b + c. Theo đầu bài, ta có: a + b + c = ⇔ 2(a + b + c) = bc (*) Do tam giác ABC vuông tại A nên ta có: a2 + b2 + c2 (định lý Py – ta – go) ⇔ a2 = (b + c)2 - 2bc ⇔ a2 = (b + c)2 - 4(a + b + c) ⇔ a2 = (b + c)2 - 4a - 4(b + c) ⇔ a2 + 4a = (b + c)2 - 4(b + c) ⇔ a2 + 4a + 4 = (b + c)2 - 4(b + c) + 4 ⇔ (a + 2)2 = (b + c - 2)2 ⇔ a + 2 = b + c - 2(b + c ≥ 2) ⇔ a = b + c - 4 Thay a = b + c – 4 vào (*) ta được: 2(b + c – 4 + b + c) = bc 4b + 4c – 8 – bc = 0 (4b – bc) + (4c – 16) = - 8 b(4 – c) + 4(c – 4) = - 8 (b – 4)(4 – c) = - 8 (b – 4)(c – 4) = 8 Vì b, c là các số nguyên dương nên ta có các trường hợp sau: TH1: TH2: Vậy có hai tam giác vuông thỏa mãn yêu cầu bài toán là hai tam giác có các kích thước là: (6, 8, 10) và (5, 12, 13). |
0,25đ 0,25đ |
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 3)
I. Phần trắc nghiệm: (3 điểm)
Câu 1: (1 điểm) Điền chữ Đ hoặc chữ S trong ô vuông tương ứng với mỗi phát biểu sau:
a. ( x + 5 )( x – 5 ) = x2 – 5
b. a3 – 1 = (a – 1 ) ( a2 + a + 1 )
c. Hình bình hành có một tâm đối xứng là giao điểm của hai đường chéo
d. Hai tam giác có diện tích bằng nhau thì bằng nhau
Câu 2: (2 điểm) Khoanh tròn chữ cái trước câu trả lời đúng nhất:
1. Đa thức x2 – 4x + 4 tại x = 2 có giá trị là:
A. 1 B. 0 C. 4 D. 25
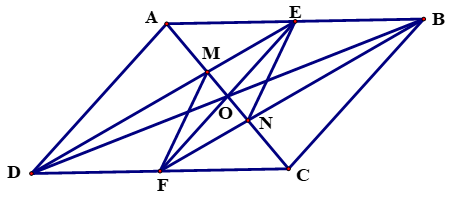
2. Giá trị của x để x ( x + 1) = 0 là:
A. x = 0 B. x = - 1 C. x = 0; x = 1 D. x = 0; x = -1
3. Một hình thang có độ dài hai đáy là 6 cm và 10 cm. Độ dài đường trung bình của hình thang đó là :
A. 14 cm B. 7 cm C. 8 cm D. Một kết quả khác.
4. Một tam giác đều cạnh 2 dm thì có diện tích là:
A. √3 dm2 B. 2√3 dm2 C. 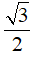 dm2 D. 6dm2
dm2 D. 6dm2
II. Phần tự luận: (7 điểm)
Bài 1: (1,5 điểm) Tính:
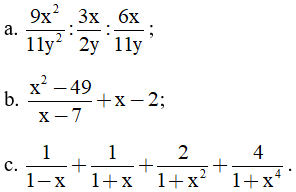
Bài 2: (1,5 điểm) Cho phân thức: A = 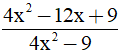
a) Tìm điều kiện xác định của phân thức A.
b) Thu gọn biểu thức A
c) Tính giá trị của biểu thức A với 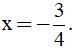 .
.
Bài 3: (3,5 điểm) Cho ΔABC vuông tại A có AH là đường cao. Từ H vẽ HD vuông góc với cạnh AB tại D, vẽ HE vuông góc với cạnh AC tại E. Biết AB = 15cm, BC = 25 cm.
a) Tính độ dài cạnh AC và diện tích tam giác ABC
b) Chứng minh tứ giác ADHE là hình chữ nhật
c) Trên tia đối của tia AC lấy điểm F sao cho AF = AE. Chứng minh tứ giác AFDH là hình bình hành
d) Gọi K là điểm đối xứng của B qua A, gọi M là trung điểm của AH. Chứng minh: CM ⊥ HK
Bài 4: (0,5 điểm) Cho các số x, y thoả mãn đẳng thức
5x2 + 5y2 + 8xy - 2x + 2y + 2 = 0 Tính giá trị của biểu thức
M = (x + y)2007 + (x - 2)2008 + (y + 1)2009
ĐÁP ÁN VÀ BIỂU ĐIỂM CHI TIẾT
Câu |
Đáp án |
Biểu điểm |
Phần I. Trắc nghiệm | ||
|
Câu 1: (Mỗi câu đúng được 0,25 điểm) 1 – S; 2 – Đ; 3 – Đ; 4 – S. Câu 2: (Mỗi câu đúng được 0,5 điểm) 1 – B; 2 – D; 3 – C; 4 – A. |
||
Phần II. Tự luận | ||
|
1 (1,0 đ) |
|
0,25 đ 0,25đ |
|
= 2x + 5. |
0,25đ 0,25đ |
|
|
0,25 điểm 0,25 điểm |
|
|
2 (2,0 đ) |
a. 4x2 - 9 ≠ 0 ⇔ (2x - 3)(2x +3) ≠ 0 ⇔
|
0,25đ |
|
0,25đ 0,25đ 0,25đ |
|
|
c. Thay
|
0,25đ 0,25đ |
|
|
3 (3,5 đ) |
- Vẽ đúng hình
(Nếu HS vẽ chưa hoàn chỉnh thì cho 0,25đ) |
0,5đ |
|
a) ΔABC vuông tại A ⇒ AB2 + AC2 = BC2 (định lý Py–ta–go) AC2 = BC2 - AB2 = 252 - 152 = 625 - 225 = 400 ⇒ AC = √400 = 20 (cm) (AC > 0)
= 150 (cm2) |
0,25đ 0,25 điểm 0,5 điểm |
|
|
b) Tứ giác ADHE có: ∠DAE = 900 (gt) ∠ADH = 900 (HD ⊥ AB) ∠AEH = 900 (HE ⊥ AC) Do đó tứ giác ADHE là hình chữ nhật (dấu hiệu nhận biết). |
0,5đ 0,5đ |
|
|
c) Ta có AF = AE (gt), AE = DH (tứ giác ADHE là hình chữ nhật) ⇒ AF = DH Tứ giác AFDH có AF // DH, AF = DH ⇒ Tứ giác AFDH là hình bình hành (dấu hiệu nhận biết). |
0,25đ 0,25đ |
|
|
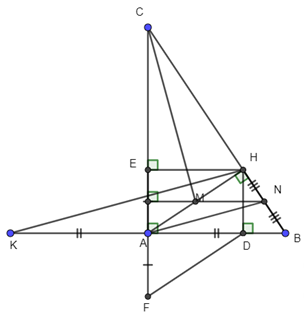
d) Gọi N là trung điểm của đoạn thẳng BH Ta có M, N lần lượt là trung điểm của AH, BH ⇒ MN là đường trung bình của tam giác HAB ⇒ MN // AB Mà AB ⊥ AC (∠A = 900) Nên MN ⊥ AC ⇒ ΔACN có MN, AH là hai đường cao cắt nhau tại M ⇒ M là trực tâm của tam giác CAN ⇒ CM là đường cao của tam giác CAN ⇒ AM ⊥ AN Mặt khác A, N lần lượt là trung điểm của BK, HB ⇒ AN là đường trung bình của tam giác BKH ⇒ AN // HK Ta có CM ⊥ AN, AN // HK Vậy CM ⊥ HK |
0,25 đ 0,25 đ |
|
|
4 (0,5 đ) |
Biến đổi 5x2 + 5y2 + 8xy - 2x + 2y + 2 = 0 ⇔ 4(x2 + 2xy + y2) + (x2 - 2x + 1) + (y2 + 2y + 1) = 0 ⇔ 4(x + y)2+ (x - 1)2 + (y + 1)2 = 0 Vì (x + y)2 ≥ 0, (x - 1)2 ≥ 0, (y + 1)2 ≥ 0 với mọi x,
Thay x = 1 và y = -1 vào M M = (x + y)2007 + (x - 2)2008 + (y + 1)2009 = 0 + 1 + 0 = 1 |
0,25 đ 0,25 đ |
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 4)
Câu 1: (1,0 điểm)
a. Nêu tính chất đường trung bình của tam giác?
b. Cho ΔABC. Gọi M là trung điểm của AB, N là trung điểm của AC, biết BC = 10cm. Tính MN.
Câu 2: (2,0 điểm) Phân tích các đa thức sau thành nhân tử.
a. 3a + 3b – a2 – ab
b. x2 + x + y2 – y – 2xy
c. - x2 + 7x – 6
Câu 3: (2,0 điểm) Thực hiện phép tính.
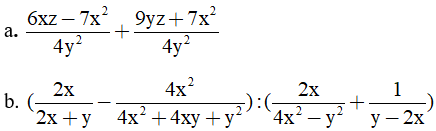
Câu 4: (2,0 điểm) Cho phân thức A = 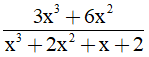
a/ Tìm điều kiện của x để giá trị của phân thức xác định.
b/ Tìm giá trị của x để phân thức có giá trị bằng 2.
Câu 5: (3,0 điểm) Cho ΔABC vuông tại A (AB < AC). Gọi I là trung điểm BC. Qua I vẽ IM ⊥ AB tại M và IN ⊥ AC tại N.
a. Tứ giác AMIN là hình gì? Vì sao?
b. Gọi D là điểm đối xứng của I qua N. Chứng minh ADCI là hình thoi.
c. Đường thẳng BN cắt DC tại K. Chứng minh 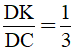 .
.
ĐÁP ÁN VÀ BIỂU ĐIỂM CHI TIẾT
Câu |
Đáp án |
Biểu điểm |
|
1 (1,0 đ) |
a. Nêu đúng tính chất ĐTB của tam giác như SGK Đường trung bình của một tam giác song song với cạnh đáy và bằng một nửa cạnh đáy. |
0,5 đ |
|
b. - Vẽ hình đúng
- Xét tam giác ABC, có: M là trung điểm của AB N là trung điểm của AC Suy ra MN là đường trung bình của tam giác ABC. Do đó MN = |
0,25đ 0,25đ |
|
|
1 (2,0 đ) |
a. - Nhóm đúng (3a +3b) – (a2 + ab) - Đặt nhân tử chung đúng 3(a + b) – a(a + b) - Đúng kết quả (a + b)(3 – a) |
0,25đ 0,25đ 0,25đ |
|
b. - Nhóm đúng (x2 – 2xy + y2) + (x – y) - Dùng đúng H ĐT (x – y)2 + (x – y) - Đúng kết quả (x – y)(x – y + 1) |
0,25đ 0,25đ 0,25đ |
|
|
c. - Tách đúng – (x2 – x – 6x + 6) = - [x(x – 1) – 6(x – 1)] = - (x – 1)(x – 6) ( Nếu HS tách đúng nhưng không làm tiếp thì vẫn cho 0,25 đ) |
0,25đ 0,25đ |
|
|
3 (2, 0 đ) |
a. - Cộng tử và giữ nguyên mẫu đúng:
- Thu gọn đúng hạng tử đồng dạng:
- Đúng kết quả |
0,25đ 0,25đ 0,5 đ |
|
b. - Quy đồng đúng trong 2 dấu ngoặc
|
0,25đ 0,25đ 0,25đ 0,25đ |
|
|
4 (2,0 đ) |
a. Biến đổi A = - Tìm đúng ĐK: x + 2 ≠ 0 ⇒ x ≠ -2 |
0,5đ 0,5đ |
|
b. Rút gọn biểu thức A:
Thay A = 2
⇔ 3x2 = 2(x2 + 1) ⇔ 3x2 = 2x2 + 2 ⇔ x2 = 2
- Kết luận: Vậy x = √2 hoặc x = -√2 |
0,25đ 0,5đ 0,25 điểm |
|
|
5 (3,0 đ) |
- Vẽ đúng hình
(Nếu HS vẽ chưa hoàn chỉnh thì cho 0,25đ) |
0,5đ |
|
a. Chứng minh đúng ANIM là hình chữ nhật có 3 góc vuông: Xét tứ giác ANIM có: ∠BAC = ∠IMA = ∠INA = 900 Suy ra tứ giác ANIM là hình chữ nhật. |
0,75đ |
|
|
b. - Giải thích được IN vừa là đường cao vừa là trung tuyến của tam giác AIC: Xét ΔAIC, có: AI = ⇒ ΔAIC cân tại I Mà IN ⊥ AC hay IN là đường cao ⇒ IN là đường trung tuyến ⇒ N là trung điểm của AC. - Chứng minh ADCI là hình bình hành có hai đường chéo vuông góc: Xét tứ giác ADCI, có: Hai đường chéo AC và AI cắt nhau tại N. Mà N là trung điểm của AC, N là trung điểm của DI. Suy ra tứ giác ADCI là hình bình hành. Mặt khác AC ⊥ DI tại N Do đó tứ giác ADCI là hình thoi. |
0,5đ 0,5đ |
|
|
c. - Kẻ thêm đường thẳng qua I song song với BK cắt CD tại E và chứng minh được EK = EC: Kẻ đường thẳng qua I song song với BK cắt CD tại E. Xét ΔBKC, có: I là trung điểm của BC (gt) IE // BK Suy ra E là trung điểm của KC hay EC = EK (1). - Chứng minh được EK = DK: Xét ΔDIE, có: N là trung điểm của DI (gt) NK // IE (BK // IE) Suy ra K là trung điểm của DE hay DK = KE (2) - Từ (1) và (2) Suy ra |
0,25đ 0,25đ 0,25đ |

Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 5)
I. Trắc nghiệm (2 điểm)
Câu 1. Tìm x, biết: x3 + 4x + x2 + 4 = 0.
A. x = 0
B. x = 2
C. x = -2
D. x = - 1
Câu 2. Tính chất nào dưới đây không phải của hình bình hành:
A. Tổng bốn góc bằng 3600.
B. Hai đường chéo bằng nhau.
C. Các cặp cạnh đối bằng nhau.
D. Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Câu 3. Hình thoi có độ dài hai đường chéo là 10cm và 24cm. Tính chu vi của hình thoi?
A. 12 cm
B. 5 cm
C. 13 cm
D. 26 cm
Câu 4. Có bao nhiêu số tự nhiên n để đa thức 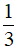 x4yn - x3y2 chia hết cho đơn thức -3xny2
x4yn - x3y2 chia hết cho đơn thức -3xny2
A. 0
B. 2
C. 1
D. 3
II. Tự luận (8 điểm)
Câu 1: (1,0 điểm) Thực hiện phép tính
a) (x + 5)2 - x(x + 10)
b) (18x6y6 - 12x5y5 + 24x3y5) : 6x3y5
Câu 2: (1,5 điểm) Phân tích đa thức sau thành nhân tử
a) a2 - b2 - 12a + 12b
b) 4x2 - 4x + 1 -25y2
c) x2 - 3x - 10
Câu 3: (2,0 điểm) Cho phân thức 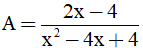 với x ≠ 2
với x ≠ 2
a) Rút gọn A
b) Tìm x nguyên để A có giá trị nguyên.
Câu 4: (3,5 điểm) Cho hình chữ nhật ABCD. Gọi M là trung điểm của BC và E là giao điểm của đường thẳng AM với đường thẳng DC.
a) Chứng minh rằng: tứ giác ABEC là hình bình hành
b) Gọi F là điểm đối xứng của B qua C. Chứng minh rằng: tứ giác BEFD là hình thoi.
c) Chứng minh rằng: C là trọng tâm tam giác AEF
d) Cho AB2 = 3BC2. Gọi H là trung điểm của DF và K là giao điểm của đường thẳng AH với đường thẳng EF. Chứng minh rằng: AE = 2MK.
ĐÁP ÁN VÀ BIỂU ĐIỂM CHI TIẾT
Câu |
Đáp án |
Biểu điểm |
|||||||||
Phần I. Trắc nghiệm | |||||||||||
|
Mỗi câu đúng được 0,5 điểm 1 – D; 2 – B; 3 – C; 4 – B. |
|||||||||||
Phần II. Tự luận | |||||||||||
|
Câu 1 (1,0 đ) |
a) (x + 5)2 - x(x + 10) = x2 + 10x + 25 - x2 - 10x = (x2 - x2) + (10x - 10x) + 25 = 25 |
0,5 đ |
|||||||||
|
b) (18x6y6 - 12x5y5 + 24x3y5) : 6x3y5 = 18x6y6 : 6x3y5 - 12x5y5 : 6x3y5 + 24x3y5 : 6x3y5 = 3x3y - 2x2+ 4 |
0,5 đ |
||||||||||
|
Câu 2 (1,5 đ) |
a) a2 - b2 - 12a + 12b = (a2 - b2) + (-12a + 12b) = (a - b)(a + b) - 12(a - b) = (a - b)(a + b - 12) |
0,5đ |
|||||||||
|
b) 4x2 - 4x + 1 -25y2 = (4x2 - 4x + 1) - (5y)2 = (2x -1)2 - (5y)2 = (2x -1 + 5y)(2x -1 - 5y) |
0,5đ |
||||||||||
|
c) x2 - 3x - 10 = x2 + 2x - 5x - 10 = x(x + 2) - 5(x + 2) = (x + 2)(x - 5) |
0,5đ |
||||||||||
|
Câu 3 (2,0 đ) |
a) |
0,5 đ |
|||||||||
|
b) Điều kiện x ≠ 2, A = A có giá trị nguyên ⇔ ⇔ 2 ⋮ (x - 2) ⇔ x - 2 là ước của của 2 ⇔ x - 2 ∈ Ư(2) = Ta có bảng sau:
Vậy x ∈ thì A có giá trị nguyên. |
0,25 đ 0,5 đ 0,5 đ 0,25 đ |
||||||||||
|
Câu 4 (3,5 đ) |
- Vẽ đúng hình
(Nếu HS vẽ chưa hoàn chỉnh thì cho 0,25đ) |
0,5đ |
|||||||||
|
a) Xét ΔABM và ΔECM có: BM = CM (M là trung điểm của BC) ∠AMB = ∠EMC (đối đỉnh), ∠ABM = ∠ECM (so le trong và AB // CD) Do đó ΔABM = ΔECM (g.c.g) ⇒ AB = EC (hai cạnh tương ứng) Mà AB // EC Do đó tứ giác ABEC là hình bình hành (dấu hiệu nhận biết) |
0,5đ 0,25 điểm 0,25 điểm |
||||||||||
|
b) Ta có AB = CD, AB = CE ⇒ CD = CE Tứ giác BEFD có: C là trung điểm của DE, C là trung điểm của BF (B và F đối xứng của C) Do đó tứ giác BEFD là hình bình hành Mà BF ⊥ DE Vậy tứ giác BEFD là hình thoi |
0,5đ 0,5đ |
||||||||||
|
c) Ta có BC = CF, CM = BM = Suy ra FC = Tam giác AEF có FM là đường trung tuyến, C thuộc đoạn thẳng FM và FC = |
0,25đ 0,25đ |
||||||||||
|
d) ΔABC vuông tại B ⇒ AB2 + BC2 = AC2 (định lí Py-ta-go) Mà AB2 = 3.BC2 Do đó AC2 = 4BC2 ⇒ AC = 2AB (AC > 0) Gọi O là giao điểm của AC, BD Ta có AC = BD, O là trung điểm của AC, BD Nên AC = BD = BF Mặt khác O, H lần lượt là trung điểm của BD, DF ⇒ HO là đường trung bình của tam giác DBF ⇒ HO = ΔHAC có HO là đường trung tuyến và ⇒ AHC = 900 Mà C, H lần lượt là trung điểm của DE, DF ⇒ CH là đường trung bình của tam giác DEF ⇒ CH // EF ⇒ ∠AKE = ∠AHC = 900 Ta có tam giác KAE vuông tại K, KM là đường trung tuyến Do đó KM = Vậy AE = 2MK |
0,25 đ 0,25 đ |
||||||||||

Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 6)
Câu 1 (1,0 điểm). Thực hiện phép tính.
a) 2x.(x2 - x + 3) b) (3 - 2x)(2x + )
Câu 2 (1,5 điểm). Phân tích các đa thức sau thành nhân tử.
a) 2x2 + 4x
b) 2(x - y) + a(y -x)
c) x2 + y2 - 2xy - 4
Câu 3 (3,0 điểm).
1) Tìm x, biết:
a) 2x2 + x = 0 b) 2x(x - 5) - x(3 + 2x) = 26
2) Tính nhanh: 342 + 162 + 32.
Câu 4 (3,0 điểm). Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD.
a) Tứ giác DEBF là hình gì? Vì sao?
b) Chứng minh rằng các đường thẳng AC, BD, EF đồng quy tại một điểm.
c) Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng M và N đối xứng nhau qua O.
Câu 5 (1,0 điểm)
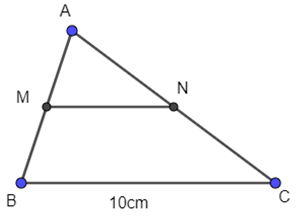
Để đo khoảng cách giữa hai điểm B và C bị ngăn bởi một cái hồ nước, người ta đóng các cọc ở vị trí A, B, C, M, N như hình vẽ. Người ta đo được MN = 55m. Tính khoảng cách BC?
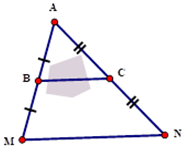
Câu 6 (0,5 điểm)
a) Cho a; b; c thoả mãn: a2022 + b2022 + c2022 = a1011b1011 + b1011c1011 + c1011a1011
Tính giá trị của biểu thức
⇒ 2(a2022 + b2022 + c2022) = 2(a1011b1011 + b1011c1011 + c1011a1011)
b) Cho ba số a, b, c thỏa mãn a + b + c = 0.
Chứng minh rằng: a4 + b4 + c4 = 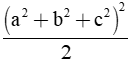
----- HẾT -----
Câu |
Nội dung |
Điểm |
|
1 (1,0 điểm) |
a) 2x.(x2 - x + 3) = 2x3 - 2x2 + 6x |
0,5 |
b) (3 - 2x).(2x + 3) = 9 - 4x2 |
0,5 |
|
|
2 (1,5 điểm) |
a) 2x2 + 4x = 2x(x + 2) |
0.5 |
|
b) 2(x - y) + a(y - x) = 2(x - y) - a(x - y) = (2 - a)(x - y) |
0.25 0.25 |
|
|
c) x2 + y2 - 2xy - 4 = (x2 + y2 - 2xy) - 4 = (x - y - 2)(x - y + 2) |
0.25 0.25 |
|
|
3 (3,0 điểm) |
1) (1,5 điểm) a) 2x2 + x = 0 ⇒ x(2x + 1) = 0
Vậy |
0.25 0.5 0.25 |
|
b) 2x(x - 5) - x(3 + 2x) = 26 ⇒ 2x2 - 10x - 3x -2x2 = 26 ⇒ -13x = 26 ⇒ x = -2 Vậy x = -2 |
0.25 0.5 0.25 |
|
|
2) (1 điểm) 342 + 162 + 32.34 = 342 + 162 + 2.16.34 = (34 + 16)2 = 502 = 2500 |
0.25 0.5 0,25 |
|
|
4 (3.0 điểm) |
- Vẽ hình đúng để làm được ý a
|
0,25 |
|
a) (1 điểm) - Chỉ ra được tứ giác DEBF là hình bình hành |
1.0 |
|
|
b) (0,75 điểm). Gọi O là giao điểm của AC và BD - Chỉ ra trong hbh ABCD có O là trung điểm O của AC và BD (1) - Chỉ ra trong hbh có BD cắt EF tại trung điểm của mỗi đường. Mà O là trung điểm của BD nên O là trung điểm của EF (2) - Từ (1) và (2) ⇒ đpcm |
0.25 0.25 0.25 |
|
|
c) (1 điểm) - Chỉ ra được M là trọng tâm của ΔABD ⇒ OM = - Chỉ ra được N là trọng tâm của ΔBCD ⇒ ON = - Mà OA = OC ⇒ OM = ON ⇒ đpcm |
0.25 0.25 0.25 0.25 |
|
|
5 (1,0 điểm) |
- Chỉ ra được BC là đường trung bình của tam giác AMN - Tính được BC = 27,5m |
0,5 0,5 |
|
6 (0,5 điểm) |
a) (0,25 điểm) Từ: a2022 + b2022 + c2022 = a1011b1011 + b1011c1011 + c1011a1011 ⇒ 2(a2022 + b2022 + c2022) = 2(a1011b1011 + b1011c1011 + c1011a1011) ⇒ (a1011 - b1011)2 + (b1011 - c1011)2 + (c1011 - a1011)2 ⇒ a = b = c ⇒ A = (a - b)2020 + (b - c)2021 + (a - c)2022 = 0 |
0.25 |
|
b) (0,25 điểm) Vì a + b + c = 0 ⇒ (a + b + c)2 = 0 ⇒ a2 + b2 + c2 + 2(ab + bc + ca) = 0 ⇒ a2 + b2 + c2 = - 2(ab + bc + ca) ⇒ (a2 + b2 + c2)2 = 4(ab + bc + ca)2 ⇒ a4 + b4 + c4 + 2(a2b2 + b2c2 + c2a2) = 4(a2b2 + b2c2 + c2a2) + 8abc(a + b + c) ⇒ a4 + b4 + c4 + 2(a2b2 + b2c2 + c2a2) + 8abc.0 (do a + b + c = 0) ⇒ 2(a4 + b4 + c4) = a4 + b4 + c4 + 2(a2b2 + b2c2 + c2a2) ⇒ 2(a4 + b4 + c4) = (a2 + b2 + c2)2 ⇒ a4 + b4 + c4 = |
0,25 |
Học sinh làm bằng cách khác đúng thì cho điểm tương tự
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 7)
I. PHẦN TRẮC NGHIỆM: ( 2,5 điểm) Hãy chọn chữ cái đứng trước câu trả lời đúng
Câu 1: Cho tứ giác ABCD, có ∠C + ∠D = 1500. Tính ∠A + ∠B = ?
A. 1300 C. 1600 B. 2100 D. 2200
Câu 2: Tứ giác có bốn góc bằng nhau, thì số đo mỗi góc là:
A. 900 B. 3600 C. 1800 D. 600
Câu 3: Hình nào sau đây vừa có tâm đối xứng, vừa có trục đối xứng ?
A. Hình bình hành B. Hình thoi C. Hình thang vuông D. Hình thang cân
Câu 4: Trong các dấu hiệu sau dấu hiệu nhận biết nào chưa đúng:
A. Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình chữ nhật.
B. Tứ giác có ba góc vuông là hình chữ nhật
C. Hình thang có một góc vuông là hình chữ nhật
D. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Câu 5: Trong tam giác vuông trung tuyến ứng với cạnh huyền có độ dài là 5cm. Độ dài cạnh huyền là:
A. 10 cm B. 2,5 cm C. 5 cm D. Cả A, B, C đều sai
Câu 6: x3 + 3x2 + 3x + 1 =
A. x3 + 1 B. (x – 1)3 C. (x + 1)3 D. (x3 + 1)3
Câu 7: Giá trị của biểu thức x(x – y) + y( x- y) tại x = 6 và y = 8:
A. 28; B. -28; C. 2; D. 14.
Câu 8: Kết quả của phép nhân: xy( x2 + x – 1) là:
A. x3y + x2y + xy;
B. x3y – x2y – xy;
C. x3y – x2y + xy;
D. x3y + x2y – xy
Câu 9: Kết quả của phép chia (20x5y – 25x3y2 – 5x3y) : 5x3y là:
A. 4x2 – 5y B. 4x2 – 5y – 1 C. 4x6y2 – 5x4y3 – x4y2 D. Một kết quả khác.
Câu 10: Giá trị của biểu thức x2 + 4x + 4 tại x = -1 là:
A. 9 B. -9 C. 1 D. 2
II. PHẦN TỰ LUẬN (7,5 điểm)
Câu 1. Tìm x, biết:
a) 3(x - 2) – 2x + 5 = 7
b) 4x2 – 25 = 0
c) 3x2 + 9x = 0
d) 5x2 – 7x -3 = 0
Câu 2. Tính

Câu 3. Cho biểu thức B = (x – 3 )(x + 3) – (x + 5)2 + (x – 1)(x + 2)
a) Rút gọn
b) Tính giá trị của biểu thức khi x = 5
Câu 4: Phân tích các đa thức sau thành nhân tử:
a) 5x2y- 10xy2
b) x2 + 2xy + y2 - 5x - 5y
c) x2 – 6x + 8
Câu 4: Cho tam giác ABC vuông tại A có đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.
a) Chứng minh tứ giác AEBM là hình thoi.
b) Cho AB = 3 cm, AC = 4 cm. Tính chu vi hình thoi AEBM
c) Tứ giác AEMC là hình gì? Vì sao?
d) Gọi I là trung điểm của AM. Chứng minh E, I, C thẳng hàng.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 8)
I. Trắc nghiệm (3 điểm)
Câu 1. Hình thang cân có cạnh bên bằng 3,5 cm, đường trung bình là 3 cm. Chu vi của hình thang cân là:
A. 6.5cm B. 13cm C. 9,5cm D. 10cm
Câu 2. Khai triển (x – 7)2 = ….. :
A. x2 – 49 B. x2 – 14x + 49 C. x2 – 2x + 49 D. x2 –7x + 49
Câu 3. Kết quả phân tích đa thức x3 + 4y + 4xy + x2 thành nhân tử là:
A. Không phân tích được.
B. x2(x + 1).4y.(x + 1)
C. x(x2 + 4y)
D. (x + 1)(x2 + 4y)
Câu 4. Khẳng định nào dưới đây đúng ?
A. Hình bình hành là hình thang cân.
B. Hình thoi là hình vuông
C. Hình chữ nhật là hình bình hành
D. Tứ giác là hình thang.
Câu 5. Tìm x, biết: (2x - 1)2 - (2x + 3)2
A. x = 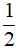
B. x = 2
C. x = -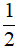
D. x = - 2
Câu 6. Cho tứ giác ABCD có số đo các góc A, B, D lần lượt là 20o , 80o , 60o Khi đó góc C bằng:
A. 1600
B. 1000
C. 2000
D. 200
II. Tự luận (7 điểm)
Bài 1 (1,5 điểm) Phân tích đa thức thành nhân tử:
a) 5x3y - 10x2y2 + 5xy33
b) x3(2y - 1) - 125(2y - 1)
c) x2 - 6x - 4y2 + 9
Bài 3 (2 điểm) Cho biểu thức C = 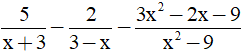
a) Tìm điều kiện xác định của biểu thức C.
b) Rút gọn biểu thức C.
c) Tìm giá trị nguyên của x để biểu thức C có giá trị nguyên.
Bài 4 (3 điểm) Cho tam giác ABC vuông tại A (AB < ) , O là trung điểm của BC. Qua O vẽ đường thẳng d vuông góc với BC cắt cạnh AC tại M. Trên tia đối của tia OM lấy điểm N sao cho O là trung điểm MN.
a) Chứng minh tứ giác MBNC là hình thoi.
b) Qua C vẽ đường thẳng song song với AB cắt tia BN tại D. Chứng minh tứ giác ABDC là hình chữ nhật rồi suy ra ba điểm A; O; D thẳng hàng.
c) Gọi AH là đường cao của tam giác ABC và E là trung điểm của BH. Đường thẳng E vuông góc với AE cắt DC tại F. Chứng minh F là trung điểm của DC.
Bài 5 (0,5 điểm)
Bác Bình cần lát gạch cho một cái sân hình chữ nhật có chiều dài là 8m, chiều rộng bằng 5m. Bác chọn các viên gạch hình vuông cạnh 4dm để lát lên sân đó. Tính số tiền mà bác Bình phải trả để mua gạch biết giá mỗi viên gạch là 95000 đồng và diện tích phần vạch sữa là không đáng kể.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 3)
I. Trắc nghiệm (3 điểm)
Bài 1 (1 điểm). Nối mỗi cụm từ ở cột A với một cụm từ ở cột B ta được câu đúng.
Cột A |
Cột B |
|
1. Tứ giác có hai cạnh đối song song và bằng nhau là 2. Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm và bằng nhau là 3. Hình thang cân có một góc vuông là 4. Hình bình hành có hai đường chéo vuông góc với nhau là |
a. Hình chữ nhật b. Hình vuông C. Hình bình hành D. Hình thoi |
Bài 2 (2 điểm). Khoanh tròn vào chữ cái đứng trước câu trả lời đúng:
1. Hình thoi có cạnh bằng 3cm. Chu vi hình thoi là:
A. 9cm B. 6cm C. 12cm D. 12cm.
2. Thực hiện phép tính (2x + y)(2x – y) :
A. 4x - y B. 4x + y C. 4x2 – y2 D. 4x2 + y2
3. Hình thang cân có đáy lớn là 4 cm, đáy bé là 3 cm. Khi đó đường trung bình của hình thang cân là:
A. 3.5 cm B. 7 cm C. 6 cm D. 1 cm
4. Điều kiện xác định của phân thức: 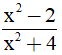
A. x ≠ ±2 B. x ≠ 2 C. x ≠ -2 D. x ∈ R
II. Tự luận (7 điểm)
Câu 1: (1 điểm) Phân tích đa thức thành nhân tử:
a) x2 - xy + 2y - 2x b) 4x2 - 4y2 + 4x + 1
Câu 2: (1 điểm) Tìm x, biết:
a) (x - 3)2 - (x + 2)(x - 1) = 0 b) 7x(x - 2) = x2 - 4
Câu 3: (2 điểm) Thực hiện các phép tính sau:
A = (x4 - x2 + 2x - 1) : (x2 + x - 1) - (x2 -x)
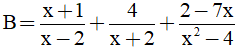
Bài 4 (3 điểm) Cho tam giác ABC vuông tại A có AM là đường trung tuyến. Kẻ MH vuông góc với AB tại H, MK vuông góc với AC tại K
a) Chứng minh tứ giác AHMK là hình chữ nhật và tính độ dài HK nếu BC = 8cm
b) Gọi E là trung điểm của MH. Chứng minh ba điểm B, E, K thẳng hàng
c) Gọi F là trung điểm của MK. Đường thẳng của HK cắt AE tại I và AF tại J. Chứng minh HI = IJ = IK
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 9)
I. Trắc nghiệm (3 điểm)
Câu 1: Cho x + y = 3. Tính giá trị của biểu thức: A = x2 + 2xy + y2 – 4x – 4y + 1
A. 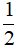
B. 1
C. 2
D. -2
Câu 2: Một tứ giác là hình bình hành nếu nó là:
A. Tứ giác có các góc kề bằng nhau
B. Tứ giác có hai cạnh đối song song và bằng nhau
C. Hình thang có hai đường chéo bằng nhau
D. Hình thang có hai đường chéo vuông góc
Câu 3: Phân tích đa thức thành nhân tử: 5x2 + 10xy – 4x – 8y
A. (5x – 2y)(x + 4y)
B. (5x + 4)(x – 2y)
C. (x + 2y)(5x – 4)
D. (5x – 4)(x – 2y)
Câu 4: Đa thức thích hợp để điền vào chỗ trống trong đẳng thức 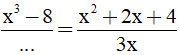 là:
là:
A. 3x(x – 2)
B. x – 2
C. 3x2(x – 2)
D. 3x(x – 2)2
Câu 5: Hình thang cân ABCD (AB // CD) có AC = 7cm, AB = 3cm, BC = 5 cm. Độ dài cạnh BD là:
A. 7cm
B. 5cm
C. 3cm
D. 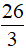 cm
cm
Câu 6: Tìm giá trị nguyên của x để phân thức 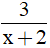 có giá trị là một số nguyên?
có giá trị là một số nguyên?
A. x = -3
B. x {-1; 1}
C. x {-1; 1; -5; -3}
D. x = -1
II. Tự luận (7 điểm)
Câu 1: (1 điểm) Phân tích các đa thức sau thành nhân tử:
a) 2x3 - 32x b) 9x2 + 6xy + y2 - 36
Câu 2: (2 điểm) Cho biểu thức: 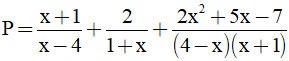 với x ≠ -1 và x ≠ 4
với x ≠ -1 và x ≠ 4
a) Rút gọn biểu thức P.
b) Tính giá trị biểu thức P khi x = 3.
c) Tìm giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
Câu 3: (1 điểm)
a) Tìm x biết: (2x + 5)2 - x2
b) Chứng minh rằng x3 + 17x chia hết cho 6 với mọi số nguyên x.
Câu 4: (2,5 điểm) Cho tam giác ABC vuông tại A (AB < AC). Vẽ đường cao AH (H ∈ ) của tam giác ABC. M là trung điểm của cạnh AB. Trên tia đối của tia MH lấy điểm D sao cho MD = MH.
a) Chứng minh rằng: tứ giác AHBD là hình chữ nhật.
b) Trên tia HC lấy điểm E sao cho HE = HB. Chứng minh rằng tứ giác ADHE là hình bình hành.
c) Gọi N là giao điểm của AH và DE, K là trung điểm của cạnh AC. Chứng minh MN // BC và ba điểm M, N, K thẳng hàng.
Câu 5: (0,5 điểm) Trên bản vẽ mảnh vườn trồng cây ăn trái của một bác nông dân có ghi lại các số liệu như sau: AD = 60cm; AC = 100cm; SABCD = 2.SADC với SABCD là diện tích mảnh vườn ABCD,SADC là diện tích phần mảnh vườn ADC (tam giác ADC vuông tại D). Bác nông dân muốn biết diện tích mảnh vườn của mình là bao nhiêu? Em hãy giúp bác tính diện tích đó? (Học sinh không cần vẽ hình lại trong bài làm)

Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 10)
I. Trắc nghiệm (3 điểm)
Câu 1: Thực hiện phép tính: (4x4 – 4x3 + 3x – 3) : (x – 1)
A. 4x2 + 3
B. 4x3 – 3
C. 4x2 – 3
D. 4x3 + 3
Câu 2: Hình thoi có độ dài hai đường chéo lần lượt bằng 12cm và 16cm. Độ dài cạnh hình thoi đó là:
A. 14cm
B. 28 cm
C. 100 cm
D. 10 cm
Câu 3: Kết quả rút gọn của phân thức 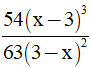 là?
là?
A. 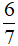 (x - 3)
(x - 3)
B. 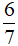 (3 - x)
(3 - x)
C. 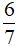 (x - 3)2
(x - 3)2
D. - 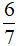 (x - 3)
(x - 3)
Câu 4: Cho T = 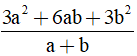 và a + b = 3. Khi đó?
và a + b = 3. Khi đó?
A. T = 27
B. T = 3
C. T = 9
D. T = 18
Câu 5: Cho hình bình hành ABCD có BC = 2AB và Â = 600. Gọi E, F theo thứ tự là trung điểm của BC và AD. Gọi I là điểm đối xứng với A qua B.
1. Tứ giác BICD là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình vuông
D. Hình bình hành
2. Số đo góc AED là:
A. 450
B. 600
C. 900
D. 1000
II. Tự luận (7 điểm)
Câu 1: (2 điểm) Cho biểu thức:
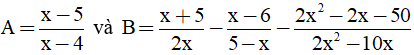 (điều kiện x ≠ 4, x ≠ 0, x ≠ ).
(điều kiện x ≠ 4, x ≠ 0, x ≠ ).
a) Tính giá trị của A khi x2 – 3x = 0.
b) Rút gọn biểu thức B.
c) Tìm giá trị nguyên của x để P = A:B có giá trị nguyên.
Câu 3: (1,5 điểm) Tìm x:
a) (3x + 1)(x -3) - x(3x - 14) = 15
b) 2x(x + 1) - 5x - 5 = 0
Câu 5. (3,5 điểm) Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH. Từ H kẻ HM vuông góc với AB (M ∈ AB), kẻ HN vuông góc với AC (N ∈ AC)
a) Chứng minh tứ giác AMHN là hình chữ nhật.
b) Gọi I là trung điểm của HC, K là điểm đối xứng với A qua I. Chứng minh AC song song HK.
c) Chứng minh tứ giác NCKM là hình thang cân.
d) MN cắt AH tại O, CO cắt AK tại D. Chứng minh AK = 3AD
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 11)
I. Trắc nghiệm (2 điểm)
Câu 1:Thực hiện phép tính sau: 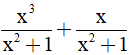
A. -x
B. 2x
C. 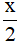
D. x
Câu 2: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Hai đường chéo AC và BD phải thỏa mãn điều kiện gì dể M, N, P, Q là bốn đỉnh của hình vuông.
A. BD = AC
B. BD ⊥ AC
C. BD tạo với AC góc 600
D. BD = AC; BD ⊥ AC
Câu 3: Tính giá trị biểu thức 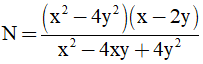 tại x = -9998 và y = -1.
tại x = -9998 và y = -1.
A. N = -9996
B. N = 10000
C. N = -10000
D. N = -19997
Câu 4: Tìm biểu thức M, biết: 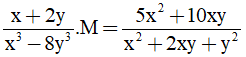
A. M = -5x(x – 2y)
B. M = 5x(x – 2y)
C. M = x(x – 2y)
D. M = 5x(x + 2y)
II. Tự luận (8 điểm)
Câu 1: (1 điểm) Phân tích đa thức thành nhân tử:
a) a3 + 8a - 4a2 - 8
b) x4 + 4
Câu 2: (1,5 điểm)
a) Thu gọn biểu thức: 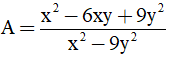
b) Thực hiện phép tính sau: 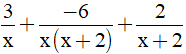
Câu 3: (1,5 điểm)
a) Tìm x biết: (x + 3)2 - (x - 2)(x + 2) = 1
b) Tìm giá trị nhỏ nhất của biểu thức M biết: M = x2 - 6x.
Câu 4: (3,5 điểm) Cho ΔABC vuông tại A có AB < AC. Gọi D, E lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm của cạnh EF.
a) Với BC = 20cm, AC = 16cm. Tính độ dài cạnh AB và độ dài cạnh DE
b) Chứng minh tứ giác BFCE là hình bình hành
c) Chứng minh tứ giác BFEA là hình chữ nhật.
d) Trên tia đối của tia EF lấy điểm K sao cho E là trung điểm cạnh FK. Chứng minh tứ giác AFCK là hình thoi.
Câu 5. (0,5 điểm) Cho ba số x, y, z thỏa mãn điều kiện:
4x2 + 2y2 + 2z2 - 4xy - 4xz + 2yz - 6y - 10z + 34 = 0.
Tính giá trị của biểu thức: T = (x - 4)2020 + (y - 4)2020 + (z - 4)2020.

Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 12)
I. Trắc nghiệm (2 điểm)
Câu 1: Điều kiện xác định của phân thức: 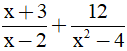
A. x ≠ 2 B. x ≠ -2 C. x ≠ ± D. x = ±2
Câu 2: Chọn câu trả lời sai. Hình bình hành có:
A. Hai đường chéo vuông góc thì là hình thoi.
B. Hai đường chéo bằng nhau là hình chữ nhật.
C. Một góc vuông là hình vuông.
D. ai cạnh bên bằng nhau là hình thoi.
Câu 3: Phân tích đa thức x2 + 3x – 6x – 18. Kết quả là:
A. (x + 6)(x – 3) B. (x – 6)(x – 3) C. (x + 6)(x + 3) D. (x – 6)(x + 3)
Câu 4: Hình thang cân ABCD có AB // CD và ∠A = 1100. Khi đó ∠B = ?
A. ∠B = 700
B. ∠B = 800
C. ∠B = 1100
D. ∠B = 1200
II. Tự luận (8 điểm)
Bài 1 (1 điểm): Thực hiện phép tính:
a) 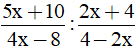
b) 5x2(4x2 – 2x + 5)
Bài 2 (1,5 điểm): Cho biểu thức P = 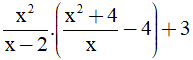 ( với x ≠ 2 ; x ≠ 0)
( với x ≠ 2 ; x ≠ 0)
a) Rút gọn P.
b) Tìm các giá trị của x để P có giá trị bé nhất. Tìm giá trị bé nhất đó.
Bài 3 (2 điểm): Tìm x, biết:
a) 5(x- 2) – 3x = 7
b) x2 – 49 = 0
c) 4x2 + 12x = 0
d) 3x 2 + 7x – 8 = 0
Bài 4 (3 điểm): Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Qua M kẻ ME ⊥ AB (E ∈ AB), MF ⊥ AC (F ∈ AC).
a) Chứng minh tứ giác AEMF là hình chữ nhật
b) Gọi N là điểm đối xứng với M qua F. Chứng minh tứ giác AMCN là hình thoi
c) Cho AB = 6cm, AC = 8cm. Tính diện tích tứ giác AEMF.
Bài 5 (0,5 điểm): Cho biểu thức 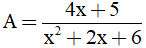 với x ∈ R. Tìm giá trị lớn nhất và giá trị nhỏ nhất của A.
với x ∈ R. Tìm giá trị lớn nhất và giá trị nhỏ nhất của A.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 13)
I. Trắc nghiệm (2,5 điểm)
Câu 1: Hình vuông có cạnh bằng 2dm thì đường chéo bằng:
A. 6 dm B. 4 dm C. √8 dm D. 2 dm
Câu 2: Giá trị của biểu thức x2 + 2x + 1 tại x = 9 là:
A. 100 B. 10 C. 1000 D. -100
Câu 3: Kết quả của phép chia (30x4y – 25x2y2 – 5x2y) : 5x2y là:
A. 6x2y– 5y + x B. 6x2 + 5y – 1 C. 6x2 – 5y – y D. 6x2 -5y – 1
Câu 4: Trong các tứ giác sau, tứ giác nào là hình có 4 trục đối xứng?
A. Hình chữ nhật B. Hình thoi C. Hình vuông D. Hình bình hành
Câu 5: Rút gọn biểu thức (a + b)2 – (a – b)2 được kết quả là:
A. 4ab B. – 4ab C. 0 D. 2b2.
Câu 6: Trong hình chữ nhật các kích thước lần lượt là 5 cm và 12 cm thì độ dài đường chéo là:
A. 17 cm B. 13 cm C. √119 cm D. Cả A, B, C đều sai
Câu 7: Câu nào đúng?
A. Hình thang có một góc vuông là hình chữ nhật.
B. Tứ giác có hai góc vuông là hình chữ nhật.
C. Tứ giác có ba góc vuông là hình chữ nhật.
D. Cả A, B , C đều đúng.
Câu 8: Hình thoi có hai đường chéo bằng 12cm và 16cm. Cạnh hình thoi là giá trị nào trong các giá trị sau:
A. 6cm B. 8cm C. 10cm D. 12cm.
Câu 9: Tính (2x – y)2
A. 2x2 – 4xy + y2;
B.4x2 – 4xy + y2;
C.4x2 – 2xy + y2;
D.4x2 + 4xy + y2
Câu 10: Kết quả của phép nhân: 2x2y.(3xy – x2 + y) là:
A. 2x3y2 – 2x4y – 2x2y2
B. 6x3y2 – 2x4y + 2x2y2
C. 6x2y – 2x5 + 2x4
D. 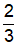 x – 2y + 2x2
x – 2y + 2x2
II. PHẦN TỰ LUẬN (7,5 điểm)
Bài 1: (1 điểm) Phân tích đa thức sau thành nhân tử
a) x2 + 3x + 3y + xy b) x3 + 5x2 + 6x
Bài 2: (1 điểm) Cho biểu thức 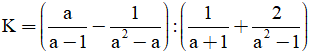
a) Tìm điều kiện của a để biểu thức K xác định và rút gọn biểu thức K
b) Tính giá trị biểu thức K khi 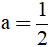
Bài 3: (2 điểm) Thực hiện phép tính:
a) (x+2)(x-1) – x(x+3)
b) 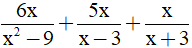
c) 2x2(3x - 5)
d) (12x3y + 18x2y) : 2xy
Bài 4: (3 điểm) Cho hình bình hành ABCD có AD = 2AB, ∠A = 600. Gọi E, F lần lượt là trung điểm BC và AD.
a) Chứng minh AE ⊥ BF.
b) Chứng minh tứ giác BFDC là hình thang cân.
c) Lấy M đối xứng của A qua B. Chứng minh tứ giác BMCD là hình chữ nhật. Suy ra M, E, D thẳng hàng.
Bài 5: (0,5 điểm) Cho các số x, y, z thỏa mãn x + y + z + xy + yz + zx = 3033. Chứng minh rằng: x2 + y2 + z2 > 2021.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 14)
I. PHẦN TRẮC NGHIỆM: (2 điểm)
Hãy chọn chữ cái đứng trước câu trả lời đúng
Câu 1. Đa thức x2 – 4x + 4 tại x = 2 có giá trị là:
A. 1 B. 0 C. 4 D. 25
Câu 2. Giá trị của x để x ( x + 1) = 0 là:
A. x = 0 B. x = - 1 C. x = 0; x = 1 D. x = 0 ; x = -1
Câu 3. Một hình thang có độ dài hai đáy là 6 cm và 10 cm. Độ dài đường trung bình của hình thang đó là :
A. 14 cm B. 7 cm C. 8 cm D. Một kết quả khác.
Câu 4. Một tam giác đều cạnh 2 dm thì có diện tích là:
A. √3 dm2 B. 2√3 dm2 C. 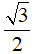 dm2 D. 6 dm2
dm2 D. 6 dm2
Câu 5: Hình chữ nhật là tứ giác:
A. Có hai cạnh vừa song song vừa bằng nhau.
B. Có bốn góc vuông.
C. Có bốn cạnh bằng nhau.
D. Có bốn cạnh bằng nhau và bốn góc vuông
Câu 6: Nhóm hình nào đều có trục đối xứng:
A. Hình bình hành, hình thang cân, hình chữ nhật.
B. Hình thang cân, hình thoi, hình vuông, hình bình hành.
C. Hình thang cân, hình chữ nhật, hình thoi, hình vuông.
D. Hình thang cân, hình chữ nhật, hình bình hành, hình vuông.
Câu 7: Khi phân tích đa thức a3 - a2x - ay2 + xy2 thành nhân tử ta được:
A. (x - a)(a - y)(a + y)
B. (a - x)(y - a)(y + a)
C. (a + x)(a - y)(a + y)
D. (a - x)(a - y)(a + y)
Câu 8. Điền vào chỗ trống: A = 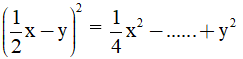
A. 2xy B. xy C.-2xy D. 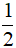 xy
xy
Câu 9: Điền đơn thức vào chỗ chấm: (3x + y)(........ – 3xy + y2) = 27x3 + y3.
A. 9x B. 6x2 C. 9x2 D. 9xy
Câu 10: Hai đường chéo của hình vuông có tính chất:
A. nhau, vuông góc với nhau.
B. nhau tại trung điểm của mỗi đường
C. Là tia phân giác của các góc của hình vuông.
D. Cả A, B, C
II. PHẦN TỰ LUẬN (8 điểm)
Bài 1 (1,5 điểm): Phân tích các đa thức sau đây thành nhân tử.
a) y2 - xy
b) x3 - 3x2y
c) 25x2 + 40x + 16
Bài 2 (2 điểm): Cho biểu thức A = 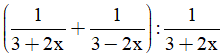
a) Tìm điều kiện của x để giá trị của biểu thức A luôn xác định.
b) Rút gọn A
c) Tính giá trị của A khi x = 3
Bài 3 (1 điểm): Tìm x biết:
a) 5( x + 2) + x( x + 2) = 0
b) (2x + 5)2 + (4x + 10)(3 – x) + x2 – 6x + 9 = 0
Bài 4 (3,5 điểm): Cho tam giác ABC ( Â = 900 ), AM là trung tuyến. Biết AB = 6cm, AC = 8cm.
a) Tính độ dài cạnh BC và AM.
b) Từ M kẻ MD vuông góc với AB. Tứ giác ADMC là hình gì? Vì sao?
c) Trên tia đối của tia DM, lấy điểm E sao cho DM = DE. Chứng minh tứ giác AEBM là hình thoi.
d) Tứ giác AEMC là hình gì? Vì sao?
e) Gọi F là điểm đối xứng với M qua AC. Chứng tỏ rằng F đối xứng với E qua điểm A.

Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 15)
I. PHẦN TRẮC NGHIỆM: ( 2,5 điểm) Hãy chọn chữ cái đứng trước câu trả lời đúng
Câu 1 : Cho các phân thức 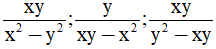 có mẫu thức chung là :
có mẫu thức chung là :
A. x2 - y2 B. x(x2 - y2) C. xy(x2 - y2) D. xy(x2 + y2)
Câu 2 : Tập các giá trị của x để 2x2 = 3x
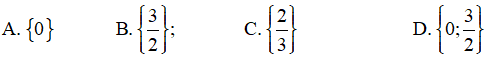
Câu 3 : Kết quả của phép tính 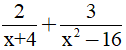 là :
là :

Câu 4: Kết quả của phép tính 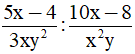 là :
là :

Câu 5: Tứ giác MNPQ là hình thoi thoả mãn điều kiện ∠M : ∠N : ∠P : ∠Q = 1 : 2 : 2 : 1, khi đó:
A. ∠M = ∠N = 600; ∠P = ∠Q = 1200
B. ∠M = ∠P = 600; ∠N = ∠Q = 1200
C. ∠M = ∠N = 1200; ∠P = ∠Q = 600
D. ∠M = ∠Q = 600; ∠N = ∠P = 1200
Câu 6: Tứ giác chỉ có một cặp cạnh đối song song và hai đường chéo bằng nhau là:
A. Hình thang cân
B. Hình chữ nhật
C. Hình vuông
D. Hình thoi .
Câu 7: Giá trị của biểu thức x2 + 4x + 4 tại x = 18 là:
A. 20 B. -400 C. 400 D. 40
Câu 8: Cho hình thang ABCD (AB//CD) có AB = 8cm; CD = 18cm. Đường trung bình MN có độ dài bằng:
A. 22cm B. 23cm C. 13 cm D. 14cm
Câu 9: Trong các tứ giác sau, tứ giác nào là hình có 4 trục đối xứng?
A. Hình chữ nhật
B. Hình thoi
C. Hình vuông
D. Hình bình hành
Câu 10: Cho hình thoi ABCD có 2 đường chéo AC = 3 cm và BD = 4cm. Độ dài canh của hình thoi đó là:
A. 2 cm B. 7 cm C. 5 cm D. 14 cm
II. PHẦN TỰ LUẬN (7,5 điểm)
Bài 1 (2 điểm): Thực hiện phép tính:
a) 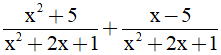
b) (6x2 - 5)(2x + 3)
c) (3x2y2 + 6x2y3 - 12xy) : 3xy
Bài 2 (1 điểm): Rút gọn rồi tính giá trị của biểu thức: 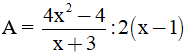 với x = 2,5.
với x = 2,5.
Bài 3 (1,5 điểm): Phân tích các đa thức sau thành nhân tử:
a) 7xy2 + 5x2y b) x2 + 2xy + y2 – 11x -11y c) x2 – x – 12
Bài 4 (3 điểm): Cho hình bình hành ABCD. Gọi I, K lần lượt là trung điểm của cạnh BC, AD.
a) Chứng minh tứ giác ABIK là hình bình hành.
b) Gọi M là giao điểm của AI và BK, N là giao điểm của CK và DI. Chứng minh BC = 2 .MN
c) Khi AC = BD và AB = 3 cm; BC = 4 cm. Hãy tính diện tích hình bình hành ABCD.
d) Chứng minh ba đường thẳng AN, DM, IK cùng đi qua một điểm G và tính độ dài GK với độ dài AB, BC đã cho ở trên.

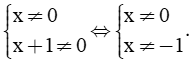
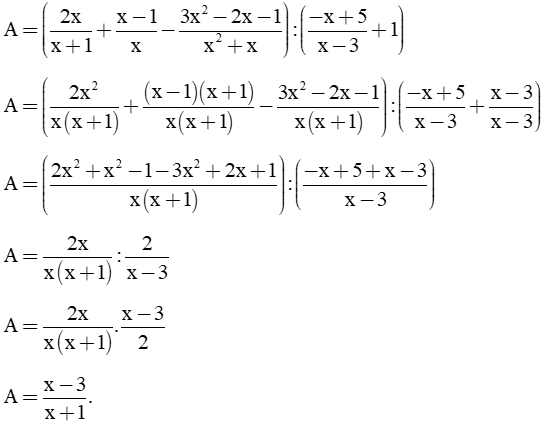
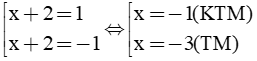
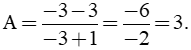
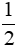
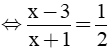
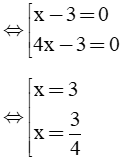
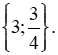
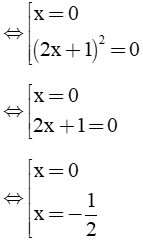
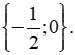
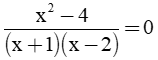
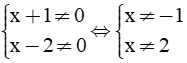
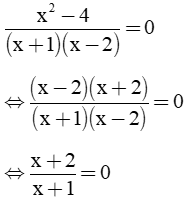
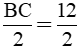 = 6cm(D là trung điểm của BC)
= 6cm(D là trung điểm của BC)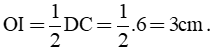
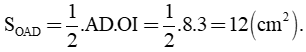
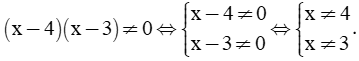
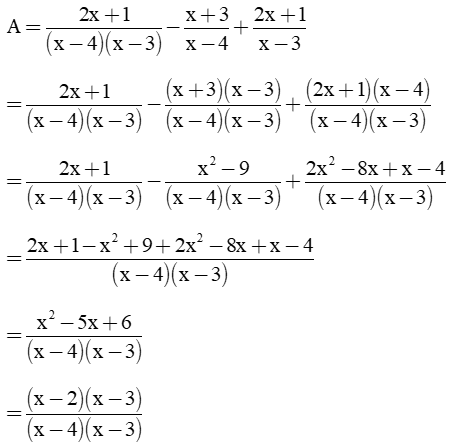
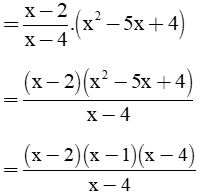
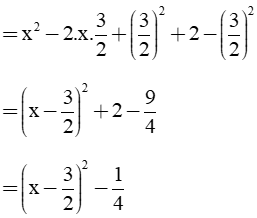
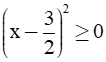 với mọi x thỏa mãn điều kiện
với mọi x thỏa mãn điều kiện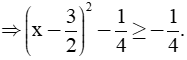
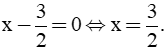
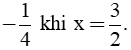
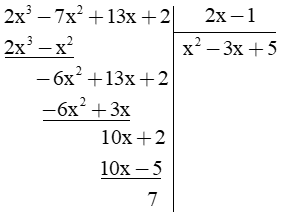
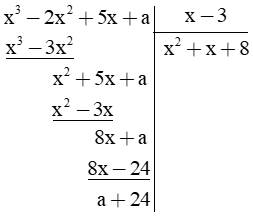
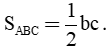 .
.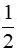 bc
bc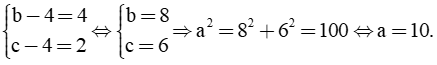
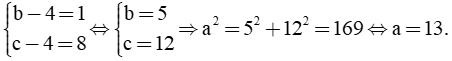
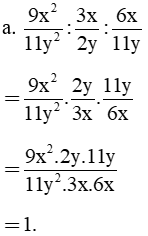
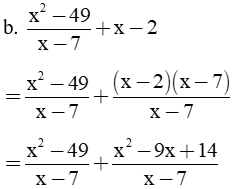
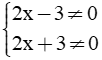
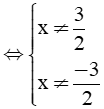
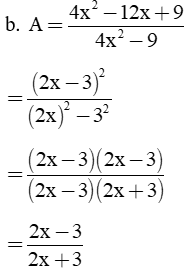
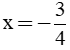 vào biểu thức A, ta được:
vào biểu thức A, ta được: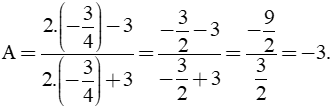
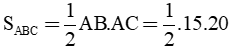
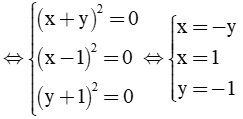
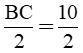 = 5cm
= 5cm
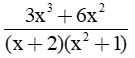
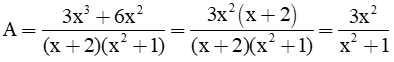
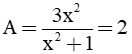
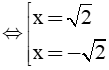 (thỏa mãn điều kiện)
(thỏa mãn điều kiện)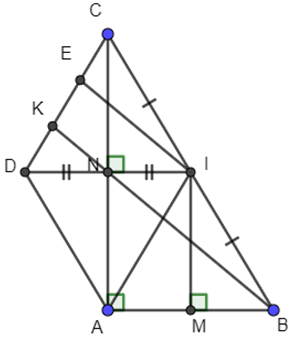
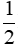 BC = IB = IC(tính chất đường trung tuyến trong tam giác vuông ABC)
BC = IB = IC(tính chất đường trung tuyến trong tam giác vuông ABC)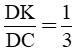
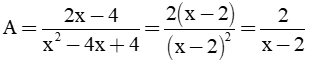
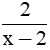
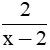 có giá trị nguyên
có giá trị nguyên
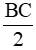 (M là trung điểm của BC)
(M là trung điểm của BC)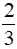 FM
FM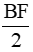
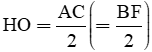 ⇒ ΔHAC vuông tại H
⇒ ΔHAC vuông tại H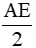
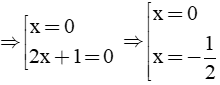
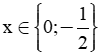
 OA
OA OC
OC