Đề thi Học kì 1 Toán lớp 8 năm 2024 có ma trận (8 đề)

---

Đề thi Học kì 1 Toán lớp 8 năm 2024 có ma trận (8 đề)

Haylamdo biên soạn và sưu tầm Đề thi Học kì 1 Toán lớp 8 năm 2024 có ma trận (8 đề) được tổng hợp chọn lọc từ đề thi môn Toán 8 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 8.

A. Ma trận

Cấp độ Chủ đề	Nhận biết		Thông hiểu		Vận dụng					Cộng
					Cấp độ thấp			Cấp độ cao
	TNKQ	TL	TNKQ	TL	TNKQ		TL	TNKQ	TL
Chương 1 Nhân, chia đa thức	Nhận biết được kết quả của một hằng đẳng thức		Hiểu được cách tính hằng đẳng thức		Tính được phép nhân đơn thức với đa thức, phân tích được đa thức thành nhân tử			Vận dụng được H ĐT để tìm GTLN
Số câu Số điểm Tỉ lệ %	1(TN1) 0,5 5%		1(TN3) 0,5 5%				3(TL1a,2a,b) 1,5 15%		1 0,5 5%	6 3,0 đ 30%
Chương2 Phân thức	Nhận biết được phân thức đối của một phân thức				Thực hiện được nhân chia cộng trừ phân thức
Số câu Số điểm Tỉ lệ %	1(TN6) 0,5 5%					4(TL1b,c,d,e) 1,75 17,5%				5 2,25đ 22,5%
Chương tứ giác	Nhận biết được tứ giác nào có trục đối xứng,tâm đối xứng		c/m tính được, tính được độ dài đường trung bình tam giác		Vẽ được hình theo yêu cầu, c/m được tứ giác là hình bình hành, hình chữ nhật, hình vuông			Vận dụng các tính chất của hình vuông hình bình hành để chứng minh đẳng thức hình học
Số câu Số điểm Tỉ lệ %	2(TN2,5) 1 10%		1 0,5 5%			1(TL4b và một phần của 4c) 1,5 15%			1(TL4c) 0,75 7,5%	5 3,75đ 37,5%
Chương đa giác-diện tích	Nhận biết được công thức tính diện tích tam giác
Số câu Số điểm Tỉ lệ %	1(TN4) 0,5 5%									1 0,5đ 5%
Tổng số câu Tổng số điểm Tỉ lệ %	5 2,5 điểm 25%		2 1,0 điểm 10%		8 4,75 điểm 47,5%			2 1,25 điểm 12,5%		17 10 điểm 100%

B. Đề thi

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 8)

Phần I: Trắc nghiệm (3,0 điểm)

Chọn câu trả lời đúng trong các câu trả lời sau. Riêng câu 10 điền vào chỗ trống để được phát biểu đúng.

Câu 1. Tính 25x³y² : 5xy². Kết quả bằng:

A. 5x²y B. 5x C. 5x² D. 5x²y

Câu 2. Cho x + y = 11, x – y = 3. Tính x² – y², ta được:

A. 14 B. 33 C. 12 D. Một kết quả khác

Câu 3. Cho 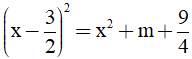Tìm m:

A. m = 3x B. m = - 3x C. m = 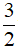x D. m = - 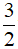x

Câu 4. Khai triển (x – y)³. Kết quả:

A. x³ + 3x²y – 3xy² – y³ B. x³ – 3x²y + 3xy² + y³

C. x³ – 3x²y + 3xy² – y³ D. (x – y)(x² + xy + y²)

Câu 5. Rút gọn phân thức 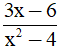. Kết quả:

Câu 6. Đa thức 3xy – x² được phân tích thành:

A. 3x(y – x) B. x(3y – x) C. x(3y – 1) D. x(3y – x²)

Câu 7. Thực hiện phép tính (6x⁴ – 3x³ + x²) : 3x². Kết quả:

A. 2x² – x + 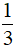B. 2x² – x + 1 C. 2x² – 3x + 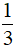D. 3x² – x +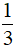

Câu 8. Hình bình hành ABCD là hình chữ nhật khi:

A. AC = BD B. AC ⊥ BD

C. AC // BD D. AC // BD và AC = BD

Câu 9. Cho hình thang ABCD có AB//CD, AB = 3cm và CD = 7cm. Gọi M; N là trung điểm của AD và BC. Độ dài của MN là:

A. 5dm B. 4cm C. 5cm D. 6cm

Câu 10. Cho hình bình hành ABCD có góc A bằng 70⁰ . Điền vào chỗ trống số thích hợp:

1. Số đo góc B là …….

2. Số đo góc C là …….

3. Số đo góc D là …….

Phần II: Tự luận (7,0 điểm)

Câu 1. (2,0 điểm). Rút gọn các biểu thức:

a) (2x + 1)² + 2(4x² – 1) + (2x – 1)² ;

b)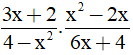

Câu 2. (2,0 điểm)

a) Phân tích đa thức sau thành nhân tử: x² – y² – 3x + 3y

b) Chứng minh rằng x² – 2x + 2 > 0 với mọi x.

Câu 3. (3,0 điểm) Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC và K là điểm đối xứng với M qua điểm I.

a) Tứ giác AKCM là hình gì?

b) Chứng minh AKMB là hình bình hành.

c) Tìm điều kiện của tam giác ABC để tứ giác AKCM là hình vuông.

----------------------Hết----------------------

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 2)

I/ PHẦN TRẮC NGHỆM (3 điểm):

Hãy chọn chữ cái đứng trước kết quả đúng ở các câu 1, 2, 3 và 4.

Câu 1: Tích (4x – 2)(4x + 2) có kết quả bằng:

A. 4x² + 4; B. 4x² – 4; C. 16x² + 4 D. 16x² – 4

Câu 2: Giá trị của biểu thứ 8x³ – 12x²y + 6xy² – y³ tại x = –10, y = –18 là:

A. – 8 ; B. 8; C. 2; D. Một giá trị khác

Câu 3: Thương của phép chia đa thức 4x² + 4x + 1 cho đa thức 2x + 1 bằng:

A. 2x – 1; B. 2x + 1; C. 2x; D. Một kết quả khác

Câu 4: Hình thang ABCD có đáy CD = 6cm; đường trung bình EF = 5cm thì:

A. AB = 5,5 cm; B. AB = 4cm; C. AB = 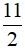cm; D. AB = 7cm.

Câu 5: Điền vào chỗ … để được kết quả đúng:

a) (2x + 3) = ……. + …….. + ………;

b) (2y - ……)² = ……… - ……… + 9x².

Câu 6: Hãy đánh dấu “X” vào ô thích hợp:

Câu	Nội dung	Đúng	Sai
a b c d e f	- Tứ giác có hai đường chéo bằng nhau là hình thang cân. - Hình thang có một góc vuông là hình chữ nhật. - Tứ giác có bốn cạnh bằng nhau và có một góc vuông là hình vuông. - Trong hình chữ nhật, giao điểm hai đường chéo cách đều bốn đỉnh của hình chữ nhật đó. - Tứ giác có hai cạnh kề bằng nhau là hình thoi. - Hình vuông có bốn trục đối xứng.

II/ PHẦN TỰ LUẬN (7 điểm):

Bài 1 (1 điểm):

a) Phân tích đa thức sau thành nhân tử: x² – y² + 2x + 1.

b) Làm tính chia: (x⁴ + 2x³ + 10x – 25) : (x² + 5).

Bài 2 (1 điểm):

a) Rút gọn biểu thức: (2x + 1)² + (3x – 2)² + 2(3x – 2)(2x +1).

b) Tìm x biết: 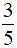x (x² – 9) = 0.

Bài 3 (1,5 điểm):

a) Quy đồng mẫu các phân thức: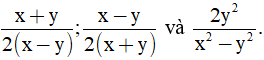

b) Tìm số tự nhiên để 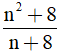là số tự nhiên.

Bài 4 (3,5 điểm): Cho ΔABC có AB = 6cm, trung tuyến AM và trung tuyến BN cắt nhau tại G. Gọi D, E lần lượt là trung điểm AG, BG.

a) Tính độ dài MN, DE.

b) Các tứ giác ABMN, ABED và DEMN là hình gì? Vì sao?

c) ΔABC cần có điều kiện gì để DEMN là hình chữ nhật và tính độ dài trung tuyến CF hạ từ đỉnh C của ΔABC để DEMN là hình vuông?

----------------------Hết----------------------

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 3)

I/ TRẮC NGHIỆM (2 điểm): (Ghi kết quả trả lời vào trong giấy làm bài) Hãy khoanh tròn vào chữ cái trước câu trả lời đúng.

Câu 1: Phân tích đa thức x³ – y³ thành nhân tử ta được:

A. (x – y)(x² + xy + y²)

B. (x + y)(x² + xy + y²)

C. (x – y)(x² – xy + y²)

D. (x + y)(x² – xy + y²)

Câu 2: Cho 8x³ – … + 6xy² – y³ = (2x – y)³. Đơn thức thích hợp điền vào dấu “…” là:

A. 6x²y B. 12x²y C. 6xy² D. 12xy²

Câu 3: Đa thức thích hợp điền vào dấu “…” trong đẳng thức 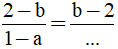là:

A. 1 + a B. 1 – a C. a – 1 D. 1 – a

Câu 4: Phân thức nghịch đảo của phân thức 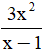là:

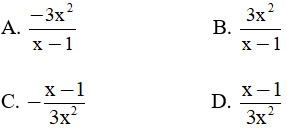
Câu 5: Cho hình vẽ bên dưới. Số đo của góc ADC là:

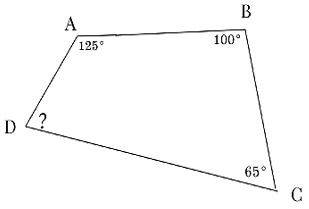
A. 85⁰ B. 80⁰ C. 75⁰ D. 70⁰

Câu 6: Hình thang cân là hình thang có:

A. Hai cạnh bên bằng nhau

B. Hai cạnh đáy bằng nhau

C. Hai góc kề một cạnh đáy bằng nhau

D. Cả hai câu A và C đều đúng

Câu 7: Chọn khẳng định đúng trong các khẳng định sau:

A. Tứ giác có hai cạnh đối song song là hình bình hành.

B. Hình bình hành có 2 đường chéo bằng nhau là hình chữ nhật.

C. Hình chữ nhật có 2 đường chéo bằng nhau là hình vuông.

D. Hình bình hành có hai cạnh đối bằng nhau là hình thoi.

Câu 8: Diện tích hình chữ nhật thay đổi thế nào nếu chiều dài tăng 4 lần và chiều rộng giảm 2 lần?

A. Diện tích hình chữ nhật tăng 2 lần.

B. Diện tích hình chữ nhật tăng 4 lần.

C. Diện tích hình chữ nhật giảm 2 lần.

D. Diện tích hình chữ nhật không đổi.

II. TỰ LUẬN: (8 điểm)

Bài 1: (2,5 điểm)

a) Làm tính nhân: 2x.(2x² + 3x – 1)

b) Làm tính chia: (2x³ + x² – 8x + 3) : (2x – 3)

c) Phân tích đa thức thành nhân tử: x³ – 4x² + 4x

d) Tìm giá trị nhỏ nhất của biểu thức: A = x² – 6x + 8

Bài 2: (2,0 điểm) Cho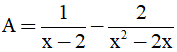

a) Tìm điều kiện của x để giá trị của phân thức A được xác định.

b) Rút gọn A.

c) Tìm số tự nhiên x để phân thức A có giá trị nguyên.

Bài 3: (3,5 điểm) Cho hình thang ABCD (AB//CD) có DC = 2AB. Gọi K là trung điểm của DC.

a) Tứ giác ABKD là hình gì? Vì sao?

b) Vẽ hình bình hành KBCH (H và B nằm khác phía đối với DC). Chứng minh A và H đối xứng nhau qua K.

c) Hình thang ABCD có thêm điều kiện gì thì tứ giác ABKD là hình chữ nhật? Khi đó hãy tính diện tích của hình thang ABCD nếu AB = 4cm, AD = 3cm.

…………………………..HẾT…………………………..

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 4)

I. Trắc nghiệm: (3 điểm)

Câu 1: Kết quả của phép tính là :

A. 4x² – 9 B. 4x² + 9 C. 4x² – 6x + 9 D. 4x² – 12x + 9

Câu 2: Kết quả phép tính 20x²y⁶z⁴ : 5xy²z² là :

A. 4x²y³z² B. 4xy⁴z² C. 4xy³z² D. 4

Câu 3: Giá trị biểu thức a³ + 3a²b + 3ab² + b³ khi a = - 3, b = 1 là:

A. -35 B. -8 C. 12 D. 10

Câu 4: Phân thức bằng với phân thức 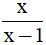là:

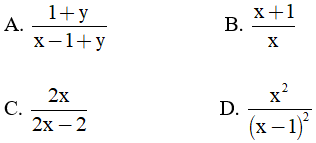
Câu 5: Mẫu thức chung của hai phân thức 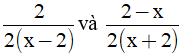là :

A. 2(x² – 4) B. (x – 2)(x + 2) C. 2(2 – x) D. 4(x² – 2)

Câu 6: Phân thức đối của phân thức 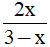là :

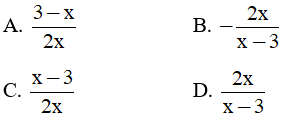
Câu 7: M, N là trung điểm các cạnh AB, AC của tam giác ABC. Khi MN = 8cm thì :

A. AB = 16cm B. AC = 16cm

C. BC = 16cm D. BC = AB = AC = 16cm

Câu 8: Số trục đối xứng của hình vuông là :

A . 4 B. 3 C. 2 D. 1

Câu 9: AM là trung tuyến của tam giác vuông ABC (∠A = 90⁰, M ∈ BC) thì:

A. AC = 2.AM B. CB = 2.AM C. BA = 2.AM D. AM =2.BC

Câu 10: Hình thang ABCD (AD // BC) có AB = 8cm, BC = 12cm, CD =10cm, DA = 4cm. Đường trung bình của hình thang này có độ dài là :

A. 10cm B. 9 cm C. 8 cm D. 7 cm

Câu 11: Theo dấu hiệu nhận biết các tứ giác đặc biệt, tứ giác có bốn cạnh bằng nhau là:

A. Hình thang vuông B. Hình thang cân C. Hình chữ nhật D. Hình thoi

Câu 12: Hình bình hành ABCD có ∠A = 2∠B. Số đo góc D là:

A. 60⁰ B. 120⁰ C. 30⁰ D. 45⁰

B. Tự luận: (7 điểm )

Bài 1 (1,5 điểm) Phân tích các đa thức thành nhân tử :

a) 5x² – 5y²;

b) x² – xy + 3x – 3y.

Bài 2 (1 điểm) Rút gọn các biểu thức:

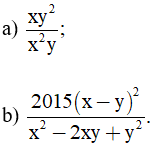
Bài 3 (1,5 điểm) Thực hiện các phép tính :

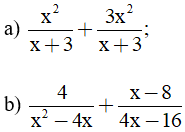
Bài 4 (3 điểm) Cho hình vuông ABCD; O là giao điểm của hai đường chéo. Đường thẳng qua O cắt cạnh AD tại E, cắt cạnh BC tại F.
a) Chứng minh ED = BF.
b) Gọi H là hình chiếu của E trên OD, P là hình chiếu của F’ trên OC, EH cắt FP tại Q. Chứng minh HP = OQ.
c) Chứng minh HP = 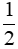EF.
d) Chứng minh ba điểm D, Q, C thẳng hàng.

Bài 5 (0,5 điểm) Cho các số a, b thỏa mãn a + b = 2 và a.b = - 2. Tính a⁷ + b⁷.

----------------------Hết----------------------

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 5)

A. TRẮC NGHIỆM: (2,0 điểm) Chọn câu trả lời đúng cho mỗi câu sau:

Câu 1. Trong hằng đẳng thức x³ – y³ = (x – y)(x² + … + y²). Số hạng còn thiếu chỗ … là:

A. xy B. 2xy C. – xy D. -2xy

Câu 2. Phân thức 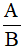bằng:

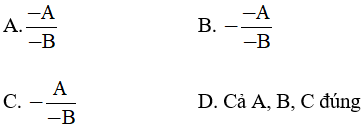
Câu 3. Rút gọn phân thức 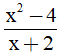, ta được:

A. x + 2 B. x – 2 C. x D. – 2

Câu 4. Điều kiện của biến x để giá trị của biểu thức 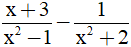xác định là:

A. x ≠ 2; x ≠ -2 B. x ≠ 1 C. x ≠ -1 D. x ≠ 1, x ≠ -1

Câu 5. Tứ giác có hai đường chéo bằng nhau và giao nhau tại trung điểm mỗi đường là hình gì ?

A. Hình chữ nhật B. Hình thoi

C. Hình bình hành D. Hình thang cân

Câu 6. Hình chữ nhật có mấy trục đối xứng ?

A. 1 B. 2 C. 3 D. 4

Câu 7. Hình nào sau đây là đa giác đều

A. Hình chữ nhật B. Hình thoi C. Hình vuông D. Cả A, B,C đúng

Câu 8. Tăng độ dài cạnh hình vuông lên ba lần thì diên tích của nó tăng mấy lần ?

A. 3 B. 6 C. 9 D. Một số khác

B. TỰ LUẬN (8.0 điểm)

Câu 1. (1,5 điểm) Phân tích các đa thức thành nhân tử:

a) x² + xy + 5x + 5y ;

b) (x² + 9)² – 36x².

Câu 2. (1,5 điểm) Tính: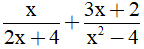

Câu 3. (2,0 điểm) Cho biểu thức: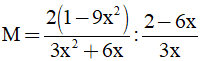

a) Rút gọn M

b) Tính giá trị của M khi x² + x = 2

c) Tìm các giá trị nguyên của x để M có giá trị nguyên

Câu 4. (3,0 điểm) Hình thang ABCD (AB // CD) có DC = 2AB. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

a) Chứng minh các tứ giác ABPD, MNPQ là hình bình hành

b) Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi.

c) Gọi E là giao điểm của BD và AP. Chứng minh ba điểm Q, N, E thẳng hàng.

----------------------Hết----------------------

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 6)

I. Trắc nghiệm (3 điểm)

Câu 1: x² - 4 bằng:

A. (x-2)(x+2) B.(x+2)(x-2) C.(x-2)(2+x) D.-(2-x)(2+x)

Câu 2: Trong các hình sau, hình nào có trục đối xứng?

A. Hình vuông B. Hình chữ nhật C. Hình thang cân D. Hình thoi

Câu 3: Kết quả của phép tính (x + y)² – (x – y)² là :

A. 2y² B. 2x² C. 4xy D. 0

Câu 4: Cho hình vẽ bên. Diện tích tích tam giác ABC bằng:

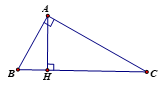
A. 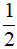AB.AC B. 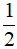AB.BC C. 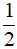AH.BC D. 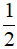AH.AB

Câu 5: Trong các hình sau, hình nào có tâm đối xứng?

A. Hình vuông B. Hình chữ nhật C. Hình thang cân D. Hình thoi

Câu 6: Phân thức đối của phân thức 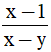là:

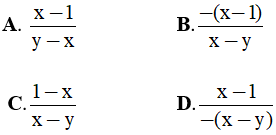
II. Tự luận

Bài 1: (2,0 điểm) Thực hiện các phép tính:

a) 2x(x² - 3);

b)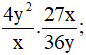

c)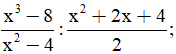

d) 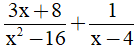( với x ≠ ± 4)

Bài 2: (1,0 điểm) Phân tích các đa thức sau thành nhân tử:

a) 2x²y + 4xy;

b) x² + y² – 1 – 2xy

Bài 3: (3,5 điểm) Cho tam giác ABC vuông tại A, AB = 4cm, AC = 8cm. Gọi E là trung điểm của AC và M là trung điểm của BC.

a) Tính EM .

b) Vẽ tia Bx song song với AC sao cho Bx cắt EM tại D. Chứng minh rằng tứ giác ABDE là hình vuông.

c) Gọi I là giao điểm của BE và AD. Gọi K là giao điểm của BE với AM. Chứng minh rằng:­­ Tứ giác BDCE là hình bình hành và DC = 6.IK.

Bài 4: (0,5 điểm) Tìm x để biểu thức sau có giá trị lớn nhất, tìm giá trị lớn nhất đó

----------------------Hết----------------------

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 7)

I. TRẮC NGHIỆM (3 điểm): Em hãy khoanh tròn chữ cái đứng trước câu trả lời mà em cho là đúng nhất trong các câu từ 1 đến 12. mỗi câu đúng 0,25 điểm

Câu 1. Kết quả của phép nhân đa thức 5x³ - x - 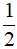với đơn thức x² là :

A. 5x⁵ - x³ + 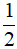x² B. 5x⁵ - x³ - 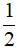x²

C. 5x⁵ + x³ + 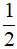x² D. 5x⁵ + x³ - 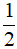x²

Câu 2. Hình thang cân có:

A. Hai góc kề một đáy bằng nhau. B. Hai cạnh bên bằng nhau.

C. Hai đường chéo bằng nhau. D. Cả A, B và C đều đúng.

Câu 3. Điều kiện xác định của phân thức 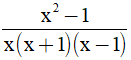là :

A. x ≠ 0 B. x ≠ 1; x ≠ -1 C. x ≠ 0; x ≠ 1; x ≠ -1 D. x ≠ 0 ; x ≠ 1

Câu 4. Giá trị của phân thức 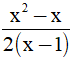tại x = 4 là :

A. 2 B. 4 C. 6 D. 8

Câu 5. Cho tam giác ABC, đường cao AH = 3cm, BC = 4cm thì diện tích của tam giác ABC là :

A. 5 cm² B. 7 cm² C. 6 cm² D. 8 cm²

Câu 6. Phép chia 2x⁴y³z : 3xy²z có kết quả bằng :

A. 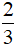x³y B. x³y

C. 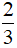x⁴yz D. 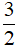x³y

Câu 7. Giá trị của biểu thức x² – 6x + 9 tại x = 5 có kết quả bằng

A. 3 B. 4 C. 5 D. 6

Câu 8. Giá trị của biểu thức 85² - 37² có kết quả bằng

A. 0 B. 106 C. – 106 D. 5856

Câu 9. Hai đường chéo hình thoi có độ dài 8cm và 10cm. Cạnh của hình hình thoi có độ dài là:

A. 6cm B. √41cm C. √164cm D. 9cm

Câu 10. Hình vuông là hình:

A. có 4 góc vuông B. có các góc và các cạnh bằng nhau

C. có các đường chéo bằng nhau D. có các cạnh bằng nhau

Câu 11. Đường trung bình MN của hình thang ABCD có hai đáy AB = 4cm và CD = 6 cm độ dài MN là :

A. 10cm B. 5cm C. 4cm. D. 6cm

Câu 12. Công thức tính diện tích tam giác (a là cạnh đáy ; h là đường cao tam giác)là

A. S = 2a.h. B. S = a.h C. S = 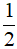a.h D. S = 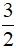a.h

II. TỰ LUẬN ( 7 điểm)

Câu 1. (2 điểm) Phân tích đa thức sau thành nhân tử:

a) x³ + 2x²y + xy² - 9x;

b) a³ – 8 – 3a + 6.

Câu 2. (1,5 điểm) Thực hiện phép tính:

a)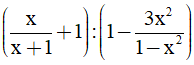

b) (x³ + 4x² + 3x + 12) : ( x + 4)

Câu 3. (1 điểm) Tìm x, biết:

a) 2x² + x = 0;

b) x³ – 8x + 1 = 0.

Câu 4. (2,5 điểm) Cho tứ giác ABCD, biết AC vuông góc với BD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA

a) Tứ giác EFGH là hình gì ? vì sao ?

b) Tính diện tích của tứ giác EFGH, biết AC = 6(cm), BD = 4(cm).

Câu 5. (0,5 điểm) Cho ba số x, y, z thỏa mãn: x² + y² + z² = xy + yz + xz và x + y + z = - 3. Tính B = x²⁰¹⁹ + y²⁰²⁰ + z²⁰²¹.

----------------------Hết----------------------

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024

Bài thi môn: Toán lớp 8

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 7)

I. TRẮC NGHIỆM (3 điểm)

Chọn chữ cái đứng trước câu trả lời đúng (2,0 điểm).

Câu 1: Kết quả của phép nhân: x(x - 2)

A. x³ – 2x² B. x² – 2x C. x² + 2x D. = x²

Câu 2: Biểu thức (a + b)² được khai triển thành:

A. a² + 2ab + b² B. a² + b² C. a² + 2ab + b² D. a² – b²

Câu 3: Kết quả của phép tính: 57² - 43² bằng:

A. 1400 B. 2400 C. 256 D. 196

Câu 4: Phân tích đa thức x³ + 1 ta có kết quả:

A. (x – 1)(x² + x + 1) B. (x + 1)³

C. (x + 1)(x² + x + 1) D. (x + 1)(x² – x + 1)

Câu 5: Rút gọn phân thức: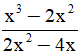

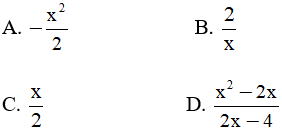
Câu 6: Mẫu thức chung của các phân thức: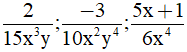

A. 30x⁴y⁴ B. 150x²y C. 30x⁹y⁵ D. 900x²y⁴

Câu 7: Tổng các góc của một tứ giác bằng bao nhiêu?

A. 540⁰ B. 180⁰ C. 360⁰ D. 720⁰

Câu 8: Cho AM là đường trung tuyến của tam giác ABC vuông tại A và AM = 3cm. Độ dài cạnh BC bằng:

A. 3cm B. 6cm C. 4 cm D. 5 cm

Câu 9: Hình thang cân ABCD có đáy nhỏ AB và số đo góc B bằng 100⁰. Khi đó số đo góc A bằng:

A. 100⁰ B. 80⁰ C. 40⁰ D. 180⁰

Câu 10: Phát biểu nào dưới đây là đúng

A. Hình bình hành có tất cả các cạnh bằng nhau.

B. Hình thoi có tất cả các góc bằng nhau

C. Hình chữ nhật có hai đường chéo vuông góc với nhau.

D. Hình thang cân có hai cạnh bên bằng nhau.

Điền vào chỗ trống nội dung thích hợp (1 điểm)

1. Gọi M và N lần lượt là trung điểm của các cạnh AB và AC của tam giác ABC, biết BC = 4cm. Khi đó độ dài đoạn thẳng MN bằng …………………………………………………

2. Hình bình hành có hai đường chéo vuông góc là hình ………………………………..

3. Trong các hình sau: hình chữ nhật, hình vuông, hình thang cân, hình tròn, hình chỉ có một trục đối xứng là: ……………………………………………………………………..

4. Hai điểm A và B đối xứng với nhau qua điểm O khi O là ……………………………

B. TỰ LUẬN: (7 điểm)

Bài 1. (1,5 điểm) Phân tích đa thức thành nhân tử:

a) a²b + 3ab

b) x² - 2x + 1

c) x³ - 6x² + 9x - xy²

Bài 2. (1 điểm)

a) Tìm x, biết: x² + 3x = 0

b) Tìm giá trị nhỏ nhất của biểu thức: x² - 4x + 7

Bài 3. (1 điểm) Rút gọn các biểu thức sau:

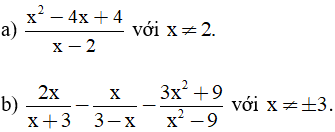
Bài 4. (3 điểm) Cho hình chữ nhật ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD.

a) Chứng minh: Tứ giác AMND là hình chữ nhật.

b) Tính diện tích của hình chữ nhật AMND biết AD = 4cm và AB = 6cm.

c) Gọi I là giao điểm của AN và DM, K là giao điểm của BN và MC. Chứng minh tứ giác MINK là hình thoi.

d) Tìm điều kiện của hình chữ nhật ABCD để tứ giác MINK là hình vuông?

Bài 5. (0,5 điểm) Tìm các số x, y, z thỏa mãn:

x² + y² + z² ≤ xy + 3y + 2z - 4

----------------------Hết----------------------