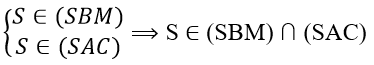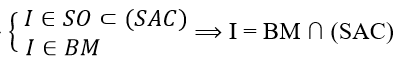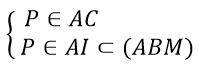Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc

Bài 1: Đại cương về đường thẳng và mặt phẳng

Bài 10 trang 54 Toán 11: Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD.

a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)

b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)

c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC)

d) Tìm giao điểm P của SC và mặt phẳng (ABM) từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)

Trả lời

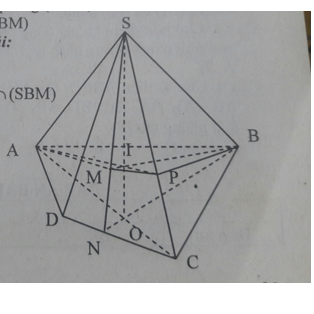
a) Gọi N = SM ∩ CD

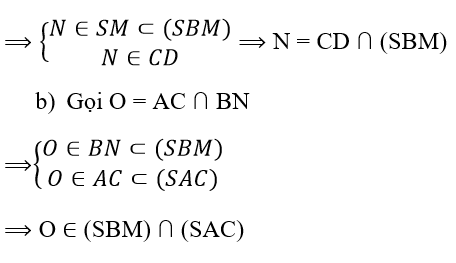
Mặt khác:

Vậy giao tuyến của (SBM) và (SAC) là đường thẳng SO.

c) Gọi I = SO ∩ BM ⇒

d) Gọi P = SC ∩ AI ⇒

⇒ P = SC ∩ (ABM) ⇒ P = (ABM) ∩ (SCD) (vì SC ⊂ (SCD))

Mặt khác M = (ABM) ∩ (SCD) ⇒ PM là giao tuyến của (SCD) và (ABM).