Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng (ABCD)

Bài 1: Đại cương về đường thẳng và mặt phẳng

Bài 9 trang 54 Toán 11: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng (ABCD) vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt đoạn BC tại E. Gọi C’ là một điểm nằm trên cạnh SC.

a) Tìm giao điểm M của CD và (C’AE)

b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C’AE)

Trả lời

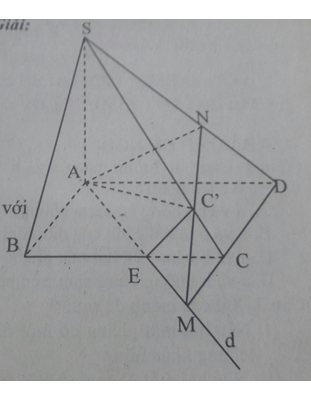
a) Vì d không song song với các cạnh của mp(ABCD)

Ta có: M = d ∩ CD = AE ∩ CD

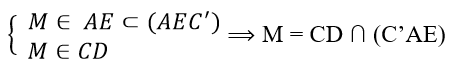
b) Gọi N = MC’ ∩ SD

Khi đó, ta có giao điểm của (C’AE) với các cạnh BC, SC, SC lần lượt là: E, C’, N

(C’AE) ∩ (ABCD) = AE

(C’AE) ∩ (SBC) = EC’

(C’AE) ∩ (SCD) = C’N

(C’AE) ∩ (SDA) = NA

Vậy thiết diện của hình chóp cắt bởi (C’AE) là tứ giác AEC’N.