Cho tứ giác ABCD nằng trong một mặt phẳng (α) có hai cạnh AB và CD không

Bài 1: Đại cương về đường thẳng và mặt phẳng

Bài 5 trang 53 Toán 11: Cho tứ giác ABCD nằng trong một mặt phẳng (α) có hai cạnh AB và CD không song song. Gọi S là điểm nằm ngoài mặt phẳng (α) và điểm M là trung điểm của đoạn thẳng SC.

a) Tìm giao điểm N của đường thẳng SD và mặt phẳng (MAB)

b) Gọi O là giao điểm của AC và BD. Chứng minh rằng ba đường thẳng SO, AM, BN đồng quy.

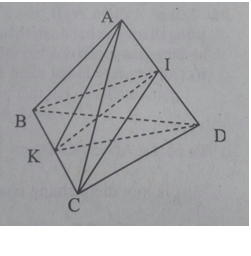
Trả lời

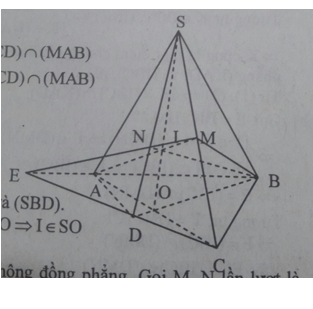
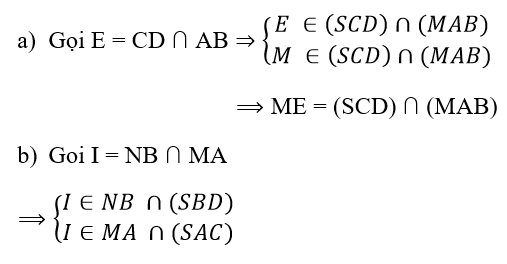
⇒ I là điểm chung của (SAC) và (SBD).

Ta cũng có: (SAC) ∩ (SBD) = SO ⇒ I ∈ SO

Vậy NB, MA, SO đồng quy.