Cho 4 điểm A, B, C và d không đồng phẳng. Gọi GA, GB, GC, GD lần lượt là

Bài 1: Đại cương về đường thẳng và mặt phẳng

Bài 4 trang 53 Toán 11: Cho 4 điểm A, B, C và d không đồng phẳng. Gọi G_A , G_B , G_C , G_D lần lượt là trọng tâm của các tam giác BCD, DCA, ABD, ABC. Chứng minh rằng: AG_A , BG_B , CG_C , DG_D đồng quy.

Trả lời

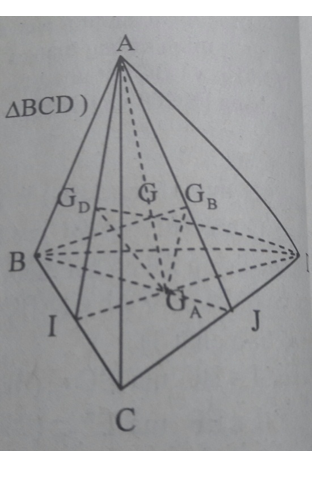
Gọi I là trung điểm của BC

Khi đó: IG_A = 1/3 ID (vì G_A là trọng tâm của ΔBCD)

IG_D = 1/3 IA (vì G_D là trọng tâm của ΔABC)

Xét ΔIAD ta có G_AG_D // AD

Gọi G = AG_A ∩ DG_D

Khi đó :

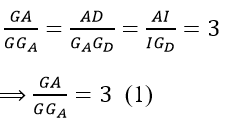
Gọi J là trung điểm của CD. Giả sử AG_A ∩ BG_B = G₁

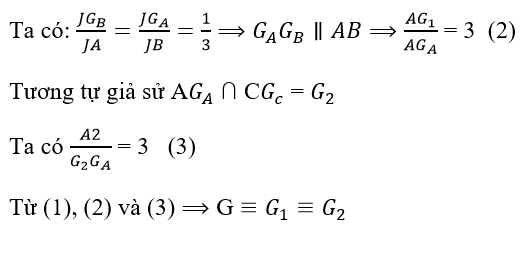
Vậy AG_A , BG_B , CG_C , DG_D đồng quy.