Cho 3 đường thẳng d1, d2, d3 không cùng nằm trong một mặt phẳng và cắt

Bài 1: Đại cương về đường thẳng và mặt phẳng

Bài 3 trang 53 Toán 11: Cho 3 đường thẳng d₁, d₂, d₃ không cùng nằm trong một mặt phẳng và cắt nhau từng đôi một. Chứng minh ba đường thẳng trên đồng quy

Trả lời

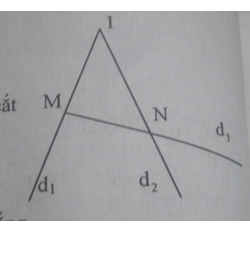
Gọi d₁,d₂,d₃ là ba đường thẳng đã cho

Gọi I = d₁ ∩ d₂

Ta chứng minh d₃ đi qua I

Giả sử d₃ không qua I. Khi đó d₃ phải cắt d₁, d₂ lần lượt tại M, N khác I

⇒ d₃ đồng phẳng với d₁, d₂

Điều này mâu thuẫn với giả thiết.

Vậy d₃ đi qua I. Vậy d₁, d₂, d₃ đồng quy tại I.