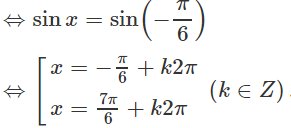Giải phương trình f′(x) = g(x) Bài 5.113 trang 217 SBT Đại số 11

Ôn tập chương 5

Bài 5.113 trang 217 Sách bài tập Đại số 11: Giải phương trình f′(x) = g(x), biết rằng

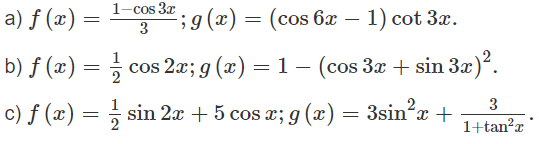
Lời giải:

a) ⇒ f′(x) = sin3x. Ta có:

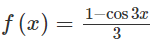
f′(x) = g(x) ⇔ (cos6x − 1).cot3x = sin3x. (điều kiện: sin3x ≠ 0 ⇔ cos3x ≠ 1 hoặc cos3x ≠ -1)

⇔ (cos6x − 1).cos3x = sin²3x

⇔ (1 − 2sin²3x − 1).cos3x = sin²3x

⇔sin²3x.(2cos3x + 1)=0

⇔ cos3x = -1/2 (vì sin3x ≠ 0)

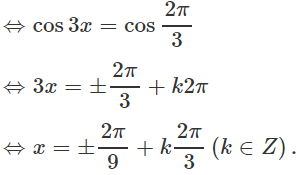
b) f(x) = cos2x/2 ⇒ f′(x) = −sin2x. Ta có

f′(x) = g(x) ⇔ −sin2x = 1 − (cos3x + sin3x)²

⇔1 + sin2x = (cos3x + sin3x)²

⇔1 + sin2x = 1 + 2sin3x.cos3x

⇔sin6x − sin2x = 0

⇔2cos4x.sin2x = 0

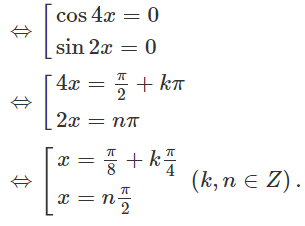
c) f(x) = sin2x/2 + 5cosx ⇒ f′(x) = cos2x − 5sinx. Ta có

f′(x) = g(x)

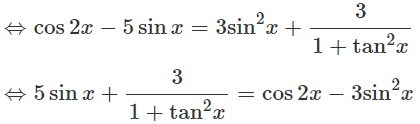
⇔5sinx + 3cos²x = cos²x − 4sin²x

⇔5sinx = −2cos²x − 4sin²x

⇔5sinx = −2 − 2sin²x

⇔2sin²x + 5sinx + 2 = 0.

Đặt t = sinx, t ∈ [−1; 1], ta có phương trình 2t² + 5t + 2 = 0.

Giải phương trình t = -0,5 ta được (loại t = -2 ).

sinx = -0,5