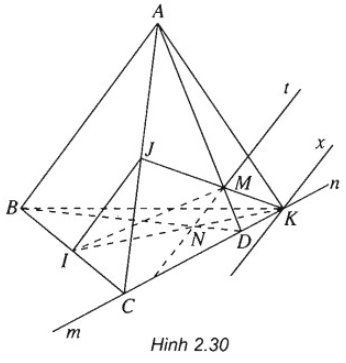
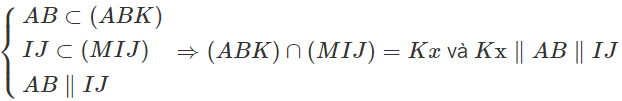Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC

Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

Bài 2.12 trang 67 Sách bài tập Hình học 11: Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC , M là một điểm tùy ý trên cạnh AD.

a) Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD)

b) Gọi N là giao điểm của BD với giao tuyến d, K là giao điểm của IN và IM. Tìm tập hợp điểm K khi M di động trên đoạn AD (M không là trung điểm của AD).

c) Tìm giao tuyến của hai mặt phẳng (ABK) và (MIJ).

Lời giải:

a)

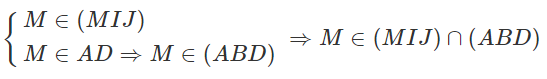
Ta cũng có:

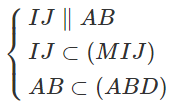
⇒ (MIJ) ∩ (ABD) = d = Mt và Mt // AB // IJ

b) Ta có: Mt // AB ⇒ Mt ∩ BD = N

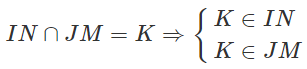
Vì K ∈ IN ⇒ K ∈ (BCD)

Và K ∈ JM ⇒ K ∈ (ACD)

Mặt khác (BCD) ∩ (ACD) = CD do đó K ∈ CD. Do vậy K nằm trên hai nửa đường thẳng Cm và Dn thuộc đường thẳng CD. ( Để ý rằng nếu M là trung điểm của AD thì sẽ không có điểm K.)

c) Ta có:

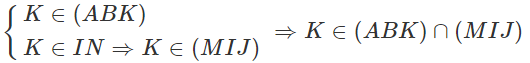
Mà