Chứng minh rằng mỗi phép quay đều có thể xem là kết quả của việc thực hiện liên tiếp hai phép đối xứng trục

Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

Bài 1.21 trang 28 Sách bài tập Hình học 11: Chứng minh rằng mỗi phép quay đều có thể xem là kết quả của việc thực hiện liên tiếp hai phép đối xứng trục.

Lời giải:

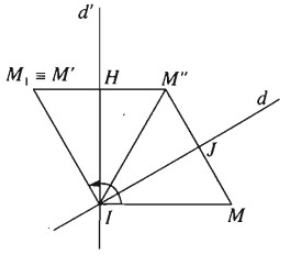
Gọi Q_(I,α) là phép quay tâm I góc α . Lấy đường thẳng d bất kì qua I. Gọi d' là ảnh của d qua phép quay tâm I góc α/2. Lấy điểm M bất kì và gọi M′ = Q_(I,α)(M). Gọi M" là ảnh của M qua phép đối xứng qua trục d. M1 là ảnh của M" qua phép đối xứng qua trục d'. Gọi J là giao của MM" với d, H là giao của M″M1 với d'. Khi đó ta có đẳng thức giữa các góc lượng giác sau:

(IM, IM₁) = (IM, IM′′) + (IM′′, IM₁)

= 2(IJ, IM′′) + 2(IM′′, IH)

= 2(IJ, IH)

= 2α/2 = a = (IM, IM′)

Từ đó suy ra M′ ≡ M₁. Như vậy M' có thể xem là ảnh của sau khi thực hiện liên tiếp hai phép đối xứng qua hai trục d và d'.