Cho hàm số y = f(x) xác định trên khoảng (a; +∞)
Bài 2: Giới hạn của hàm số
Bài 4.26 trang 166 Sách bài tập Đại số 11: Cho hàm số y = f(x) xác định trên khoảng (a; +∞)
Chứng minh rằng nếu
thì luôn tồn tại ít nhất một số c thuộc (a; +∞) sao cho f(c) < 0
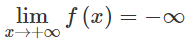
Lời giải:
Vì
nên với dãy số (xn) bất kì, xn > a và xn → +∞
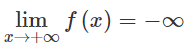
ta luôn có
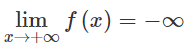
Do đó
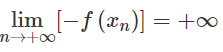
Theo định nghĩa suy ra −f(xn) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 2 thì −f(xn)>2 kể từ một số hạng nào đó trở đi.
Nói cách khác, luôn tồn tại ít nhất một số xk ∈ (a;+∞) sao cho −f(xk ) > 2 hay f(xk) < −2 < 0
Đặt c = xk ta có f(c) < 0
