Cho hai điểm B, C cố định nằm trên đường tròn (O ; R)

Bài 3: Phép đối xứng trục

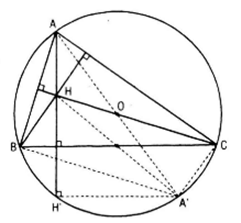
Bài 10 (trang 13 sgk Hình học 11 nâng cao): Cho hai điểm B, C cố định nằm trên đường tròn (O ; R) và điểm A thay đổi trên đường tròn đó . Hãy dùng phép đối xứng trục để chứng minh rằng trục tâm H của tam giác ABC nằm trên một đường tròn cố định.

Hướng dẫn : Khi BC không phải là đường kính, gọi H’ là giao điểm của đường thẳng AH với đường tròn (O; R). Chứng minh rằng H đối xứng với H’ qua đường thẳng BC.

Lời giải:

Trường hợp BC là đường kính thì H trùng A, do đó H nằm trên đường tròn cố định (O; R)

Xét trường hợp BC không là đường kính. Giả sử đường thẳng AH cắt đường tròn (O; R) tại H’. Như vậy với mỗi điểm A Є (O; R) khác với B và C thì ta xác định điểm H’Є (O; R) . Gọi AA’ là đường kính của đường tròn (O; R) thì A’B // CH (Vì cùng vuông góc với AB) và A’C//BH (vì cùng vuông góc AC) nên A’BHC là hình bình hành. Vậy BC đi qua trung điểm của HA’ . Mặt khác BC//A’H’(Vì cùng vuông góc với AH) nên BC cùng đi qua trung điểm của HH’.

Do đó H và H’ đối xứng với nhau qua BC. Nếu gọi Đ là đối xứng có trục là đường thẳng BC thì Đ biến H’ thành H. Nhưng H’ luôn luôn nằm trên (O; R) nên H nằm trên đường tròn cố định là ảnh hưởng của đường tròn (O; R) qua phép đối xứng trục Đ

Cách khác:gọi H’ là điểm đối xứng của H qua BC . Chứng minh tứ giác ABH’C nội tiếp, từ đó suy ra H’ nằm trên (O; R)