Một vật nặng treo bởi 1 chiếc lò xo chuyển động lên xuống qua vị trí cân bằng

Bài 3: Một số dạng phương trình lượng giác đơn giản

Bài 31 (trang 41 sgk Đại Số và Giải Tích 11 nâng cao): Một vật nặng treo bởi 1 chiếc lò xo chuyển động lên xuống qua vị trí cân bằng. Khoảng cách h từ vật đó đến vị trí cân bằng ở thời điểm t giây được tính theo công thức h = |d| trong đó d = 5sin6t - 4cos6t, với d được tính bằng cm, ta quy ước d > 0 khi vật ở trên vị trí cân bằng, d < 0 khi vật ở dưới vị trí cân bằng. Hỏi:

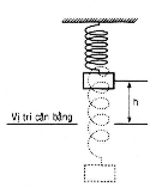
a) Ở vào thời điểm nào trong 1 giây đầu tiên vật ở vị trí cân bằng?

b) Ở vào thời điểm nào trong 1 giấy đầu tiên, vật ở xa vị trí cân bằng nhất?

(Tính chính xác đến 1/100 giây).

Lời giải:

Ta có :

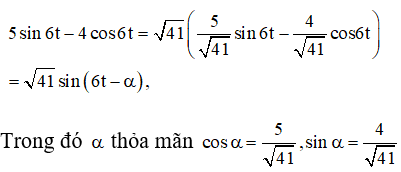
Sử dụng bảng số hoặc máy tính bỏ túi ta tìm được α ≈ 0,675.

a) Vật ở vị trí cân bằng khi d = 0, nghĩa là sin(6t - α) = 0

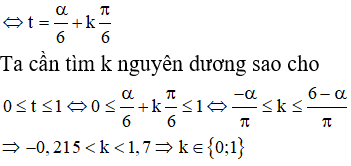
Vậy trong khoảng thời gian 1 giây đầu tiên có 2 lần vật ở vị trí cân bằng là t ≈ 0,11 giây (ứng với k = 0) và t ≈ 0,64 giây (ứng với k = 1).

b) Vật ở xa vị trí cân bằng nhất khi |d| nhận giá trị lớn nhất. Điều đó xảy ra nếu sin(6t - α) = ±1 . Ta có:

Vậy trong khoảng thời gian 1 giây đầu tiên có 2 lần vật ở xa vị trí cân bằng nhất là t ≈ 0,37 giây (ứng với k = 0) và t ≈ 0,90 giây (ứng với k = 1).