Cho góc nhọn xOy và môt điểm A năm trong góc đó . Hãy xác định điểm B trên Ox

---

Bài 3: Phép đối xứng trục

Bài 9 (trang 13 sgk Hình học 11 nâng cao): Cho góc nhọn xOy và môt điểm A năm trong góc đó . Hãy xác định điểm B trên Ox và điểm C trên Oy sao cho tam giác ABC có chu vi nhỏ nhất

Lời giải:

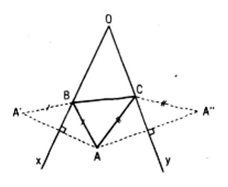
Xét tam giác bất kì ABC có B và C lần lượt nằm trên hai tia Ox và Oy. Gọi A’ và A’’ là các điểm đối xứng với điểm A lần lượt qua các đường thẳng Ox và Oy .

Ta có AB = A’B và AC = A’’C (do các ΔABA’ và ΔACA” là các tam giác cân ).

Gọi 2p là chu vi của tam giác ABC thì :

2p = AB+BC+CA=A’B+BC+CA” ≥A’A”

Dấu “=” xảy ra khi bốn điểm A’, B, C , A” thẳng hàng .

Suy ra để chu vi tam giác ABC bé nhất thì phải lấy B và C lần lượt là giao điểm của đoạn thẳng A’A” với hai tia Ox và Oy (các giao điểm đó tồn tại vì góc xOy nhọn)