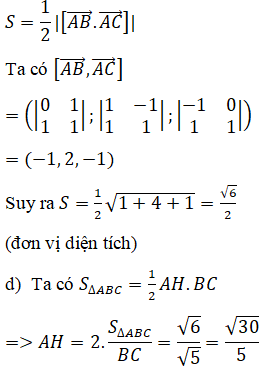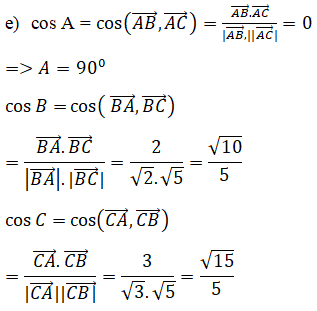Cho ba điểm A(1, 0, 0), B(0, 0, 1), C(2, 1, 1) a) Chứng minh A, B, C không thẳng hàng

Bài 1: Hệ tọa độ trong không gian

Haylamdo biên soạn và sưu tầm lời giải Bài 10 trang 81 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 10 (trang 81 sgk Hình Học 12 nâng cao): Cho ba điểm A(1, 0, 0), B(0, 0, 1), C(2, 1, 1)

a) Chứng minh A, B, C không thẳng hàng.

b) Tìm tọa độ điểm D để ABCD là hình bình hành.

c) Tính độ dài đường cao của tam giác ABC.

d) Tính độ dài đường cao của tam giác ABC kẻ từ đỉnh A.

e) Tính các góc của tam giác ABC.

Lời giải:

a) Ta có AB→=(-1,0,1), AC→=(1,1,1), ta thấy AB→ và AC→ không cùng phương nên A, B, C không thẳng hàng.

b) Gọi D = (x, y, z), ta có AD→=(x-1,y,z),BC→=(2,1,0). Để ABCD là hình bình hành thì AD→=BC→, hay

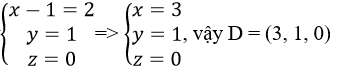
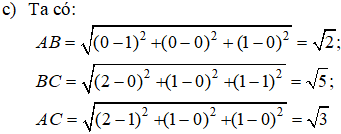
Chu vi ΔABC là: P=AB+BC+AC=√2+√5+√3

Diện tích ΔABC là: