Tìm tọa độ tâm và bán kính mặt cầu sau đây: x^2+y^2+z^2-8x+2y+1=0

Bài 1: Hệ tọa độ trong không gian

Haylamdo biên soạn và sưu tầm lời giải Bài 13 trang 82 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 13 (trang 82 sgk Hình Học 12 nâng cao): Tìm tọa độ tâm và bán kính mặt cầu sau đây:

a) x²+y²+z²-8x+2y+1=0

b) 3x²+3y²+3z²+6x-3y+15z-2=0

c) 9x²+9y²+9z²-6x+18y+1=0

Lời giải:

a) Ta có: x²+y²+z²-8x+2y+1=0

<=> (x-4)²+(y+1)²+z²=16

Nên mặt cầu có tâm la I(4, -1, 0) và bán kính R = 4.

b) Ta có: 3x²+3y²+3z²+6x-3y+15z-2=0

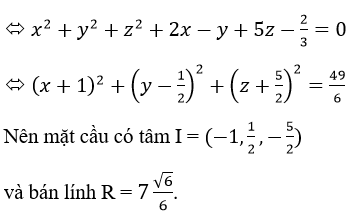
c) Ta có: 9x²+9y²+9z²-6x+18y+1=0

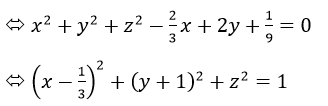
Nên mặt cầu có tâm là I = (1/3; -1,0) và bán kính R = 1.