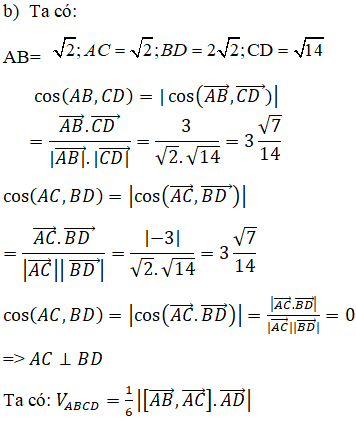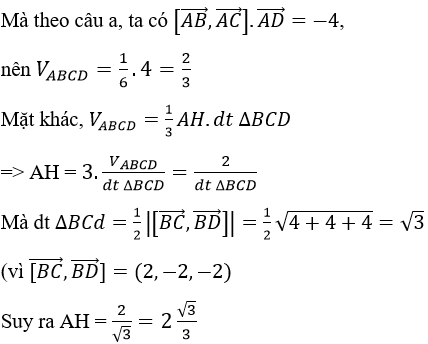Cho bốn điểm A(1, 0, 0), B(0, 1, 0), C(0, 0, 1) và D(-2, 1, -2). Chứng minh rằng A, B, C, D là bốn đỉnh

Bài 1: Hệ tọa độ trong không gian

Haylamdo biên soạn và sưu tầm lời giải Bài 11 trang 81 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 11 (trang 81 sgk Hình Học 12 nâng cao): Cho bốn điểm A(1, 0, 0), B(0, 1, 0), C(0, 0, 1) và D(-2, 1, -2).

a) Chứng minh rằng A, B, C, D là bốn đỉnh của một hình tứ diện.

b) Tính góc bởi các cạnh đối của tứ diện đó. Tính thể tích tứ diện ABCD và độ dài đường cao của tứ diện kẻ từ đỉnh A.

Lời giải:

a) Ta có AB→=(-1,1,0),AC→=(-1,0,1),AD→=(-3,1,-2) nên ta có: [AB→,AC→ ]=(1,1,1), suy ra [AB→,AC→ ].AD→=-4 ≠ 0. Vậy A, B, C, D không đồng phẳng, hay A, B, C, D là bốn đỉnh của tứ diện.