Tìm tọa độ điểm M thuộc Ox sao cho M cách đều hai điểm A(1, 2, 3) và B(-3, -3, 2)

Bài 1: Hệ tọa độ trong không gian

Haylamdo biên soạn và sưu tầm lời giải Bài 8 trang 81 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 8 (trang 81 sgk Hình Học 12 nâng cao):

a) Tìm tọa độ điểm M thuộc Ox sao cho M cách đều hai điểm A(1, 2, 3) và B(-3, -3, 2)

b) Cho ba điểm A(2, 0, 4) và B(4, √3, 5) và C(sin 5t, cos 3t, sin 3t). Tìm t để AB vuông góc với OC (O là gốc tọa độ).

Lời giải:

a) Gọi M = (a, 0, 0) thuộc Ox thỏa mãn MA = MB.

Ta có: MA²=(1-a)²+4+9=a²-2a+14

MB²=(3+a)²+9+4=a²+6a+22

Để MA = MB thì MA²=MB² <=> a²-2a+14=a²+6a+22 <=> a = -1

Vậy M = (-1, 0, 0) là điểm cần tìm.

b) Ta có AB→=(2,√3,1),OC→=(sin⁡5t,cos⁡3t,sin⁡3t)

Để AB⊥OC thì AB→.OC→=0 <=>2 sin⁡5t+√3 cos⁡3t+sin⁡3t=0

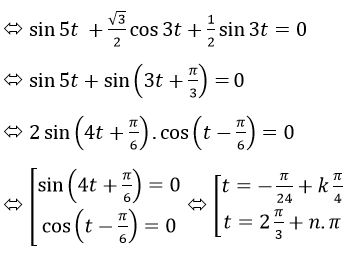
Với k, n ∈ Z

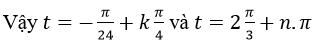
với n, k ∈Z là những giá trị cần tìm.