Hãy chia một khối tứ diện thành hai khối tứ diện sao cho tỉ số thể tích của hai khối này bằng số k > 0
Bài 4: Thể tích của khối đa diện
Haylamdo biên soạn và sưu tầm lời giải Bài 16 trang 28 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.
Bài 16 (trang 28 sgk Hình Học 12 nâng cao): Hãy chia một khối tứ diện thành hai khối tứ diện sao cho tỉ số thể tích của hai khối này bằng số k > 0 cho trước.
Lời giải:
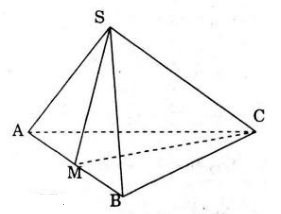
Gọi M là một điểm trên đoạn thẳng AB. Khi đó (SMC) chia tứ diện S.ABC thành hai tứ diện S.AMC và S. BMC lần lượt với thể tích V1,2
Vì d(S, (AMC) = d(S,(BMC)) nên
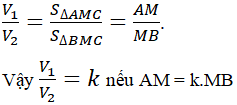
Kết luận: Lấy điểm M trên AB sao cho AM = k.MB. Khi đó, khối tứ diện SABC được chia thành hai khối tứ diện SAMC và SBMC thỏa yêu cầu bài toán.

