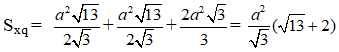Cho khối lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác đều cạnh a. điểm A’ cách đều 3 điểm A, B, C

Bài 4: Thể tích của khối đa diện

Haylamdo biên soạn và sưu tầm lời giải Bài 20 trang 28 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 20 (trang 28 sgk Hình Học 12 nâng cao): Cho khối lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác đều cạnh a. điểm A’ cách đều 3 điểm A, B, C, cạnh bên AA’ tạo với mặt phẳng đáy một góc 60⁰.

a) Tính thể tích của khối lăng trụ đó.

b) Chứng minh rằng mặt bên BCC’B’ là một hình chữ nhật.

c) Tính tổng diện tích các mặt bên của hình lăng trụ ABC.A’B’C’ (tổng đó gọi là diện tích xung quanh của hình (hoặc khối lăng trụ đã cho).

Lời giải:

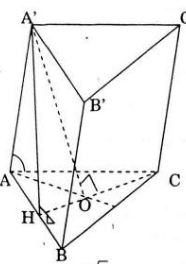
a) Gọi O là tâm của tam giác ABC, vì OA = OB = OC nên A' O ⊥ (ABC)

Suy ra, OA = OB = OC

Lại có: A’A = A’B = A’C

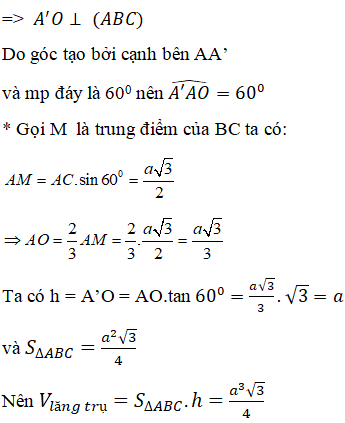
b) Ta có: BC ⊥ AO nên BC ⊥ AA' (định lí 3 đường vuông góc)

Lại có AA’ //CC’ => BC ⊥ CC’

Tứ giác BB’C’C là hình bình hành có một góc vuông nên là hình chữ nhật.

c) Gọi H là trung điểm của AB .

Ta có: AB⊥(A^' HO)nên A^' H⊥AB

Trong tam giác vuông A’OH có:

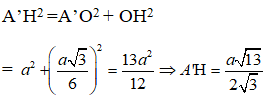
Diện tích hình bình hành ABB’A’ là :

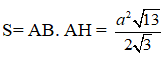
Tương tự, diện tích hình bình hành ACC’A’ là:

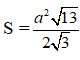
Diện tích hình chữ nhật BCC’B’ là

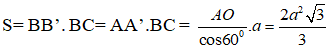
Vậy diện tích xung quanh của hình lăng trụ là: