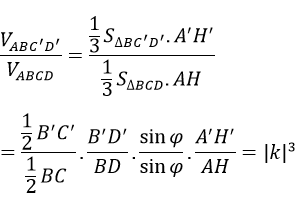Chứng minh rằng nếu có phép vị tự số k biến tứ diện ABCD thành tứ diện A’B’C’D’ thì

Bài 4: Thể tích của khối đa diện

Haylamdo biên soạn và sưu tầm lời giải Bài 25 trang 29 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 25 (trang 29 sgk Hình Học 12 nâng cao): Chứng minh rằng nếu có phép vị tự số k biến tứ diện ABCD thành tứ diện A’B’C’D’ thì:

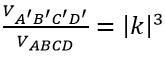
Lời giải:

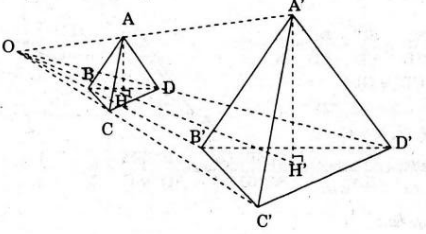
Gọi H là hình chiếu của A trên (BCD). Giả sử phép vị tự tỉ số k biến A, B, C, D, H lần lượt thành A’, B’, C’, D’, H’.

Hơn nữa, theo tính chất của phép vị tự thì:

A’H’ song song hoặc trùng hợp với AH;

Và (B’C’D’) song song hoặc trùng hợp với (BCD)

Mà AH ⊥ (BCD) nên A'H'⊥(B'C'D').

Vậy A’H’ là đường cao của tứ diện (A’B’C’D’) (1)

Mặt khác, dễ thấy:

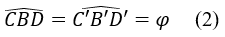
Hơn nữa, cũng từ tính chất của phép vị từ ta có:

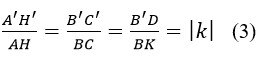
Từ (1), (2), (3) ta có: