Cho điểm M nằm trong hình tứ diện đều ABCD. Chứng minh rằng tổng các khoảng cách
Bài 4: Thể tích của khối đa diện
Haylamdo biên soạn và sưu tầm lời giải Bài 21 trang 28 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.
Bài 21 (trang 28 sgk Hình Học 12 nâng cao): Cho điểm M nằm trong hình tứ diện đều ABCD. Chứng minh rằng tổng các khoảng cách từ M tới bốn mặt của hình tứ diện là một số không phụ thuộc vào vị trí của điểm M. Tổng đó bằng bao nhiêu nếu cạnh của tứ diện đều bằng a?
Lời giải:
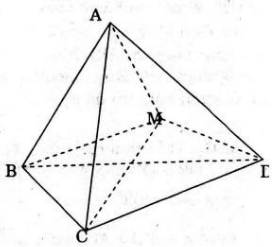
Gọi h1,h2,h3,h4 lần lượt là khoảng các từ M đến (ABC), (ACD), (ABD), (BCD). Khối tứ diện ABCD được chia thành 4 khối tứ diện MABC, MACD, MABD, MBCD.
Ta có:
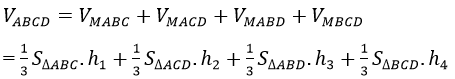
Lại vì SΔABC=SΔACD=SΔABD=SΔBCD
Nên VABCD=(1/3).S_ΔABC (h1+h2+h3+h4) (1)
Gọi h là chiều cao của tứ diện đều, ta có:
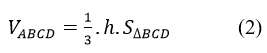
Từ (1) và (2) có: h1+h2+h3+h4=h
Vậy khoảng cách từ M đến 4 mặt của hình tứ diện là một số không phụ thuộc vào vị trí của M.
* Xét tứ diện đều ABCD có cạnh là a. Ta tính h.
Gọi là trực tâm của tam giác đều BCD và M là trung điểm của CD
Ta có:


