Xác định vị trí tương đối giữa các cặp đường thẳng d và d’ cho bởi phương trình

Bài 3: Phương trình đường thẳng

Haylamdo biên soạn và sưu tầm lời giải Bài 28 trang 103 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 28 (trang 103 sgk Hình Học 12 nâng cao): Xác định vị trí tương đối giữa các cặp đường thẳng d và d’ cho bởi phương trình:

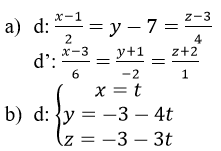
d’: là giao tuyến của hai mặt phẳng: (α):x+y-z=0

(α' ):2x-y+2z=0

Lời giải:

a) Đường thẳng d đi qua M₀(1,7,3)và có vectơ chỉ phương u→=(2,1,4) đường thẳng (d’) đi qua M₀'(3,-1,-2) và có vectơ chỉ phương u'→=(6,-2,1)

nên ta tính được

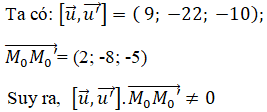
Vậy d và d’ chéo nhau.

b) Thay x, y, z ở phương trình tham số của d vào phương trình (α) ta được: t-3-4t+3+3t=0 <=> 0 = 0 (đúng với ∀t)

Vậy d ⊂ (α) (1)

Thay x, y, z ở phương trình tham số của d vào phương trình (α') ta được:

2t+3+4t-6-6t=0 <=> -3=0 (vô nghiệm)

Vậy d // α' (2)

Từ (1) và (2) suy ra: d // d’