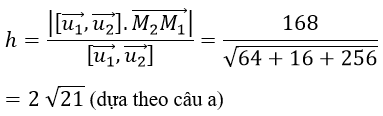Cho hai đường thẳng: trang 103 sgk Hình Học 12 nâng cao

Bài 3: Phương trình đường thẳng

Haylamdo biên soạn và sưu tầm lời giải Bài 31 trang 103 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 31 (trang 103 sgk Hình Học 12 nâng cao): Cho hai đường thẳng:

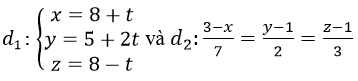
a) Chứng tỏ rằng hai đường thẳng đó chéo nhau

b) Viết phương trình mặt phẳng đi qua gốc tọa độ O và song song với d₁ và d₂.

c) Tính khoảng cách giữa hai đường thẳng d₁ và d₂.

d) Viết phương trình vuông góc chung của hai đường thẳng đó.

Lời giải:

a) Đường thẳng (d₁) đi qua M₁ (8,5,8) và có vectơ chỉ phương là u₁→=(1,2,-1)

Đường thẳng (d₂) đi qua M₂ (3,1,1) và có vectơ chỉ phương là u₂→=(-7,2,3)

Ta có:

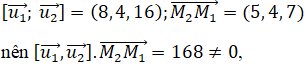
suy ra d₁ và d₂ chéo nhau. (đpcm)

b) Mặt phẳng đi qua O(0, 0, 0) và song song với d₁ và d₂ sẽ nhận vectơ u₁u₂→=(8,4,16) làm vectơ pháp tuyến, nên đường trình của mặt phẳng đó là: 8(x-0)+4(y-0)+16(z-0)=0 <=> 2x+y+4z=0

c) Khoảng cách giữa d₁ và d₂ là: