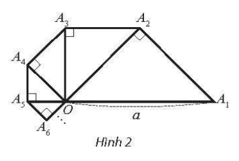
Cho tam giác OA1A2 vuông cân tại A2 có cạnh huyền OA1 bằng a

❮ Bài trước Bài sau ❯

Cho tam giác OAA vuông cân tại A có cạnh huyền OA bằng a. Bên ngoài tam giác OAA, vẽ tam giác OAA vuông cân tại A. Tiếp theo, bên ngoài tam giác OAA, vẽ tam giác OAA vuông cân tại A. Cứ tiếp tục quá trình như trên, ta vẽ được một dãy các hình tam giác vuông cân (Hình 2). Tính độ dài đường gấp khúc AAAA...

Giải sách bài tập Toán 11 Bài 1: Giới hạn của dãy số - Chân trời sáng tạo

Bài 11 trang 76 SBT Toán 11 Tập 1: Cho tam giác OA₁A₂ vuông cân tại A₂ có cạnh huyền OA₁ bằng a. Bên ngoài tam giác OA₁A₂, vẽ tam giác OA₂A₃ vuông cân tại A₃. Tiếp theo, bên ngoài tam giác OA₂A₃, vẽ tam giác OA₃A₄ vuông cân tại A₄. Cứ tiếp tục quá trình như trên, ta vẽ được một dãy các hình tam giác vuông cân (Hình 2). Tính độ dài đường gấp khúc A₁A₂A₃A₄...

Lời giải:

Ta có các góc $\hat{A_{1} O A_{2}}, \hat{A_{2} O A_{3}}, \hat{A_{3} O A_{4}}, \dots$ đều bằng 45°. Ta có:

$A_{1} A_{2} = O A_{2} = O A_{1} \cdot cos 45^{\circ} = a \frac{\sqrt{2}}{2};$

$A_{2} A_{3} = O A_{3} = O A_{2} \cdot cos 45^{\circ} = a \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2}}{2} = a {(\frac{\sqrt{2}}{2})}^{2}$

$A_{3} A_{4} = O A_{4} = O A_{3} \cdot cos 45^{\circ} = a {(\frac{\sqrt{2}}{2})}^{2} \cdot \frac{\sqrt{2}}{2} = a {(\frac{\sqrt{2}}{2})}^{3}$

Vậy độ dài các đoạn thẳng A₁A₂, A₂A₃, A₃A₄, ... tạo thành cấp số nhân lùi vô hạn với số hạng đầu $u_{1} = \frac{a \sqrt{2}}{2}$ và công bội $q = \frac{\sqrt{2}}{2}$ thỏa mãn |q| < 1.

Do đó, độ dài đường gấp khúc A₁A₂A₃A₄... là

$l = \frac{a \sqrt{2}}{2} \cdot \frac{1}{1 - \frac{\sqrt{2}}{2}} = \frac{a \sqrt{2}}{2 - \sqrt{2}} = \frac{a \sqrt{2}}{2} \cdot (2 + \sqrt{2}) = a (1 + \sqrt{2}) .$

Lời giải Sách bài tập Toán lớp 11 Bài 1: Giới hạn của dãy số hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯